Indice | Previo: Fundamentos.Calculo | Siguiente: Fundamentos.Calculo.CalculoInfinitesimal
4.1.1. Conjunto, tuplas y vectores¶
Hay tres tipos de entidades matemáticas (además de los números reales y las funciones) que usaremos con frecuencia en este capítulo (y en general en todo el libro):
Conjuntos. Muchas veces nos referiremos aquí a conjuntos (no necesariamente ordenados) de entidades que están relacionadas de alguna manera: las coordenadas de un punto en el espacio de fases, un conjunto de funciones, las ecuaciones diferenciales que describen el movimiento de un sistema dinámico, las partículas que interactúan gravitacionalmente en un sistema, etc. Los elementos de la mayoría de los conjuntos usados en este libro estarán numerados. Así por ejemplo, las masas de un sistema de N partículas, $m_0$, $m_1$, ..., $m_{N-1}$ se representarán como el conjunto:
$$ \{m_i\}_{i=0,1,\ldots,N-1} $$
Una versión sintética más común de esta notación será $\{m_i\}_N$. En el caso en el que el número de elementos sea claro en el contexto se usará simplemente $\{m_i\}$
Nota: Numeración comenzando en cero. En lo sucesivo numeraremos todas las cantidades físicas y matemáticas (partículas, variables auxiliares, componentes de un vector o una matriz, etc.) comenzando en cero, tal y como se acostumbra en programación. Esta elección facilitará la implementación de las fórmulas en algoritmos y programas de computadora. Si bien la numeración comenzando en cero no es muy común en matemáticas o física, existen justificaciones poderosas para su uso, algunas de las cuáles están enumeradas en el documento "Why numbering should start at zero" del maestro de maestros de la programación científica, Edsger Wybe Dijkstra.
Tuplas. Las tuplas (pares, tripletas, etc.) son conjuntos ordenados de números reales. Para las tuplas usaremos la notación convencional $(x_0,x_2,\ldots,x_{N-1})$, donde los paréntesis, a diferencia de las llaves de los conjuntos más generales, nos permitirán reconocer el hecho de que el orden de los elementos es importante. Las tuplas forman, con el conjunto de los números reales, un espacio vectorial. En este espacio se definen las siguientes operaciones básicas:
Suma:
\begin{equation} \label{eq:suma_tuplas} (a_0,a_1,\ldots)+(b_0,b_1,\ldots)\equiv(a_0+b_0,a_1+b_1,\ldots) \end{equation}
Multiplicación por un escalar:
\begin{equation} \label{eq:k_tupla} k(a_0,a_1,\ldots)\equiv(ka_0,ka_1,\ldots) \end{equation}
donde $k$ es un número real.
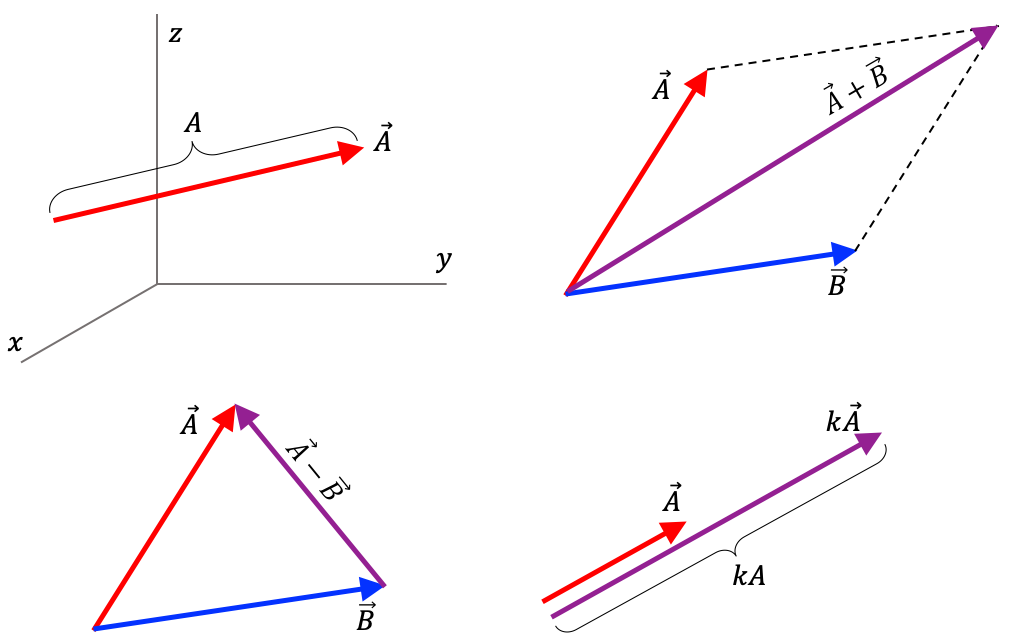
Vectores geométricos (euclidianos). Los vectores geométricos o en breve vectores, son segmentos orientados en el espacio de tres dimensiones (ver Figura (vectores)) que tienen las siguientes propiedades:
Se denotarán en este libro como $\vec A$ o $\hat e$ (este último es un vector unitario) en lugar de usar la notación más común con letras en negrilla.
Todo vector tiene: 1) magnitud, $A$, igual a la longitud (euclidiana) del segmento correspondiente y 2) una dirección en el espacio.
Los vectores forman con los números reales, un espacio vectorial con operaciones definidas, geométricamente, como se muestra en la Figura (vectores).
El elemento neutro de la operación suma entre vectores, es el vector nulo, que representaremos como $\vec 0$.
Todo vector, por definición, se puede escribir como una combinación lineal de tres vectores de una base ortonormal: $\hat{e}_0,\hat{e}_1,\hat{e}_2$. Los coeficientes de la combinación se conocen como componentes del vector:
\begin{equation} \label{eq:vectores_en_base} \vec A=A_0\hat{e}_0+A_1\hat{e}_1+A_2\hat{e}_2. \end{equation}
El espacio de vectores es isomorfico a el espacio vectorial de tripletas. Por la misma razón nos referiremos al vector, o bien como la entidad abstracta $\vec A$, como su representación en términos de los vectores unitarios de una base ortonormal (ver ítem anterior) o aún mejor, en términos de la tripleta:
$$ \vec A:(A_0,A_1,A_2) $$
En este caso usaremos el símbolo ":" en lugar de "=" para dar entender que el vector no es una tripleta sino una entidad geométrica más abstracta.
El isomorfismo implica también, que las componentes de los vectores en las operaciones geométricas definidas en la Figura (vectores), cumplen la Ecs. (suma_tuplas) y (k_tupla).
Además de la suma y la multiplicación por un escalar, que caracterizan el espacio vectorial, se definen dos productos adicionales:
Producto escalar o producto punto, $\vec A\cdot\vec B$. El producto escalar se define, a partir los vectores unitarios de la base, como:
$$\hat{e}_i\cdot \hat{e}_j=\delta_{ij},$$
donde $\delta_{ij}$ es el "delta de kroenecker":
\begin{equation} \label{eq:delta_kroenecker} \delta_{ij}=\left\{ \begin{array}{ccc} 1 & & i=j\\ 0 & & i\neq j\\ \end{array} \right. \end{equation}
Con esta esta definición y usando la representación de los vectores dada por la Ec. (vectores_en_base) puede probarse que:
$$ \vec A\cdot\vec B=A_0B_0+A_1B_1+A_2B_2 $$
Producto vectorial o producto cruz, $\vec A\times\vec B$. El producto vectorial se define, a partir los vectores unitarios de la base, como:
\begin{equation} \label{eq:base_mano_derecha} \hat{e}_i\times \hat{e}_j=\epsilon_{ijk}\hat{e}_k, \end{equation}
donde $\epsilon_{ijk}$ es el "simbolo de Levi-Civita" ("levi chivita"):
\begin{equation} \label{eq:levi_civita} {\epsilon _{ijk}=\left\{{\begin{matrix}+1&{\mbox{si }}(i,j,k){\mbox{ es }}(0,1,2),(1,2,0){\mbox{ o }}(2,0,1)\\-1&{\mbox{si }}(i,j,k){\mbox{ es }}(2,1,0),(0,2,1){\mbox{ o }}(1,0,2)\\0&{\mbox{de otro modo }}i=j{\text{ o }}j=k{\text{ o }}k=i\end{matrix}}\right.} \end{equation}
Al conjunto de vectores unitarios de una base que se definen cumpliendo la Ec. (base_mano_derecha) se lo llama un conjunto de vectores de mano derecha.
Con esta esta definición y usando la representación de los vectores dada por la Ec. (vectores_en_base) puede probarse que:
\begin{equation} \label{eq:producto_cruz} \begin{array}{rcl} \vec A\times\vec B & = & (A_1B_2-A_2B_1)\hat{e}_0+\\ & & -(A_0B_2-A_2B_0)\hat{e}_1+\\ & & (A_0B_1-A_1B_0)\hat{e}_2\\ \end{array} \end{equation}
Está última expresión es tan elaborada que con frecuencia se usa la regla mnemoténica:
\begin{equation} \label{eq:producto_cruz_determinante} \vec A\times\vec B = \left| \begin{array}{ccc} \hat{e}_0 & \hat{e}_1 & \hat{e}_2\\ A_0 & A_1 & A_2\\ B_0 & B_1 & B_2\\ \end{array} \right| \end{equation}
Donde $|M|$ es el determinante de la matriz $M$.
Otras identidades útiles:
Propiedad cíclica del triple producto escalar:
\begin{equation} \label{eq:triple_producto_escalar} \vec A\cdot(\vec B\times\vec C)= \vec C\cdot(\vec A\times\vec B)= \vec B\cdot(\vec C\times\vec A) \end{equation}
Triple producto vectorial:
\begin{equation} \label{eq:triple_producto_vectorial} \vec A\times(\vec B\times\vec C)=(\vec A\cdot\vec C)\vec B-(\vec A\cdot\vec B)\vec C \end{equation}
Algoritmos para conjuntos y tuplas¶
Todos los lenguajes modernos de programación, definen tipos especiales para representar conjuntos y tuplas. En Python existen tres tipos de objetos básicos para este propósito: listas, tuplas y diccionarios. Existen sútiles diferencias entre las listas y las tuplas en Python y en general usaremos con más frecuencia las primeras.
Para para los algoritmos de este libro, es importante entender las operaciones entre listas, que son diferentes a las operaciones en el espacio vectorial de las tuplas matemáticas que definimos antes.
Así, por ejemplo, en el siguiente algorítmo se construye una lista con las componentes del vector de estado de una partícula, "sumando" las listas de las componentes de su vector posición y velocidad:
#Lista de componentes del vector posición
r=[1,0,3]
#Lista de componentes del vector velocidad
v=[0,-1,0]
#Lista de componentes del vector de estado
X=r+v
El operador +, entre listas y tuplas de Python produce la unión de los elementos de las listas.
Usando este operador se pueden hacer algoritmos prácticos como el que se muestra a continuación:
def f(x):
from math import sin
y=sin(x)/x
return y
valores_de_x=[1.0,2.0,3.0]
valores_de_f=[]
for x in valores_de_x:
valores_de_f+=[f(x)]
aquí, comenzamos con un conjunto vacío, valores_de_f=[] y después, dentro de un ciclo, usamos el operador de acumulación += para agreganr elementos al conjunto. Este es un método muy común usado en el lenguaje para construir "tablas de valores", que pueden, por ejemplo usarse para hacer gráficos de funciones.
Algoritmos para vectores¶
Los vectores forman un "capítulo" en la computación separado de las listas y las tuplas. La razón básica son sus propiedades matemáticas y las operaciones definidas entre ellos. Bibliotecas de rutinas muy completas existen en todos los lenguajes de programación para representar este tipo de entidades matemáticas.
En Python y a lo largo de este libro usaremos los objetos y rutinas de los paquetes NumPy y SPICE para definir y manipular vectores.
El ejemplo abajo muestra como se calcula el ángulo entre dos vectores $\theta_{AB}$, a partir de la interpretación geométrica del producto punto $\vec{A}\cdot\vec{B}=AB\cos\theta_{AB}$ (ver problemas al final del capítulo):
#Definimos los vectores
from numpy import array
A=array([1.0,0.0,2.0])
B=array([0.0,1.0,3.0])
#Calculamos el producto escalar y vectorial
from numpy import dot
ApuntoB=dot(A,B)
#El ángulo entre los vectores
from numpy import arccos
from numpy.linalg import norm
anguloAB=arccos(ApuntoB/(norm(A)*norm(B)))
Nota: Radianes y grados en los algoritmos. Es importante entender que las funciones trigonométricas inversas como arccos, devuelven, en todos los lenguajes de programación, valores de los ángulos en radianes. En el caso anterior, por ejemplo, el valor de la variable anguloAB al final del algoritmo en realidad era 0.5575988266995369. Sin embargo, decidimos mostrar su valor en grados después de multiplicar anguloAB por el factor de conversión $\pi/180$ (esta operación no se muestra en el código.) Así lo seguiremos haciendo en el resto del libro. El lector que use los algoritmos no debe olvidar multiplicar por el factor de conversión para reconstruir los resultados mostrados aquí.
Un procedimiento similar, esta vez usando vectores y rutinas de SPICE (internamente SPICE usa vectores o arreglos de NumPy), puede usarse para calcular el triple producto vectorial:
from numpy import array
from spiceypy import vdot,vcrss
A=array([2.0,2.0,1.0])
B=array([0.0,-1.0,0.0])
C=array([0.0,0.0,2.0])
AxBxC=vdot(A,B)*C-vdot(A,C)*B
También podemos usarlas para verificar la propiedad cíclica del triple producto escalar:
from numpy import array
from spiceypy import vnorm,vdot,vcrss
A=array([2.0,2.0,1.0])
B=array([0.0,-1.0,0.0])
C=array([0.0,0.0,2.0])
ABC=vdot(A,vcrss(B,C))
CAB=vdot(C,vcrss(A,B))
BCA=vdot(B,vcrss(C,A))
Con lo que se verifica la identidad (al menos para los vectores escogidos.)
4.1.2. Sistemas de coordenadas¶
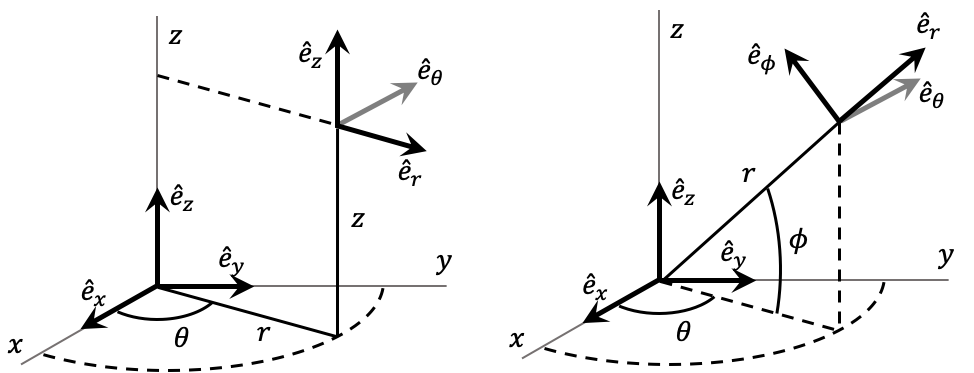
A lo largo de este libro, usaremos los tres sistemas de coordenadas ortogonales clásicos (cartesianas, cilíndricas y esféricas, ver Figura (coordenadas)) con algunas convenciones más propias de la astronomía y la mecánica celeste que del cálculo.
A continuación, y en especial para clarificar nuestra notación, enumeramos detalladamente las propiedades de cada sistema.
Sistema de coordenadas cartesiano.
- Coordenadas: $x\in(-\infty,+\infty)$, $y\in(-\infty,+\infty)$, $z\in(-\infty,+\infty)$.
- Vectores unitarios: $\hat{e}_x$, $\hat{e}_y$, $\hat{e}_z$.
Comentarios:
- En todos los casos la orientación de los ejes obedecerá la regla de la mano derecha, es decir, los sistemas cartesianos usados en el texto y cuyos ejes están definidos por el conjunto de vectores unitarios ($\hat{e}_x$, $\hat{e}_y$, $\hat{e}_z$) forman un conjunto de mano derecha (ver Ec. base_mano_derecha), a saber, en forma explícita:
\begin{equation} \label{eq:conjunto_mano_derecha} \begin{array}{ccl} \hat{e}_x\times\hat{e}_y & = & \hat{e}_z\\ \hat{e}_y\times\hat{e}_z & = & \hat{e}_x\\ \hat{e}_z\times\hat{e}_x & = & \hat{e}_y \end{array} \end{equation}
Sistema de coordenadas cilíndrico (ver Figura (coordenadas)).
Coordenadas: $r\in[0,+\infty)$, $\theta\in[0,2\pi)$, $z\in(-\infty,+\infty)$.
Conversión al sistema de coordenadas cartesianas:
\begin{equation} \label{eq:cilindricas_a_cartesianas} \begin{array}{ccl} x & = & r\cos\theta\\ y & = & r\sin\theta\\ \end{array} \end{equation}
Vectores unitarios expresados en el sistema de coordenadas cartesianas:
\begin{equation} \label{eq:unitarios_cilindricas} \begin{array}{ccl} \hat{e}_r & = & \cos\theta\;\hat{e}_x + \sin\theta\;\hat{e}_y\\ \hat{e}_\theta & = & -\sin\theta\;\hat{e}_x + \cos\theta\;\hat{e}_y\\ \hat{e}_z & = & \hat{e}_z \end{array} \end{equation}
Comentarios:
El conjunto de vectores unitarios ($\hat{e}_r$, $\hat{e}_\theta$, $\hat{e}_z$) forman un conjunto de mano derecha tal y como se definió en las Ecs. (conjunto_mano_derecha).
Nótese que, a diferencia de la notación usada generalmente en los textos de cálculo, la coordenada cilíndrica $r$ usa la misma letra que la coordenada esférica $r$ y la magnitud del vector posición (ver siguiente sección). La distinción entre las tres, dependerá del contexto.
Usaremos la letra griega $\theta$ para denotar el ángulo acimutal, a diferencia de la notación convencional que usa esta letra para la coordenada esférica polar (ángulo del vector posición respecto al eje z.)
Sistema de coordenadas esférico (ver Figura (coordenadas)).
Coordenadas: $r\in[0,+\infty)$, $\theta\in[0,2\pi)$, $\phi\in[-\pi/2,+\pi/2]$.
Conversión al sistema de coordenadas cartesianas:
\begin{equation} \label{eq:esfericas_a_cartesianas} \begin{array}{ccl} x & = & r\cos\phi\cos\theta\\ y & = & r\cos\phi\sin\theta\\ z & = & r\sin\phi\\ \end{array} \end{equation}
Vectores unitarios expresados en el sistema de coordenadas cartesianas:
\begin{equation} \label{eq:unitarios_esfericas} \begin{array}{ccl} \hat{e}_r & = & \cos\phi\cos\theta\;\hat{e}_x + \cos\phi\sin\theta\;\hat{e}_y + \sin\phi\;\hat{e}_z\\ \hat{e}_\theta & = & -\sin\theta\;\hat{e}_x + \cos\theta\;\hat{e}_y\\ \hat{e}_\phi & = & \cos\phi\cos\theta\;\hat{e}_x + \sin\phi\sin\theta\;\hat{e}_y - \sin\phi\;\hat{e}_z\\ \end{array} \end{equation}
Comentarios:
El conjunto de vectores unitarios ($\hat{e}_r$, $\hat{e}_\theta$, $\hat{e}_\phi$) forman un conjunto de mano derecha tal y como se definió en las Ecs. (conjunto_mano_derecha).
Nótese que, a diferencia de la notación usada generalmente en los textos de cálculo, la coordenada esférica $\phi$ se medirá respecto al plano $x-y$ (como una latitud) en lugar de hacerlo respecto al eje $z$ (como una colatitud).
Una interesante página interactiva que permite visualizar mejor la definición de los sistemas de coordenadas y la orientación de los vectores coordenadas puede encontrarse en los siguientes enlaces, tanto para el sistema de coordenadas cilíndrica como para el sistema de coordenadas esféricas.
Indice | Previo: Fundamentos.Calculo | Siguiente: Fundamentos.Calculo.CalculoInfinitesimal