Indice | Previo: Fundamentos.Calculo.EcuacionesDiferenciales | Siguiente: Fundamentos.Calculo.Series

4.1.9. Funcionales y cálculo de variaciones

Un tema poco cubierto en los textos básicos de cálculo, pero de gran utilidad en la mecánica, es el denominado cálculo de variaciones. Si bien en esta sección de "repaso" no pretendemos ofrecer una introducción detallada a esta importante área del análisis matemático, es necesario presentar aquí algunos resultados básicos que serán de utilidad para el resto del libro.

Si el cálculo infinitesimal, que repasamos en las secciones anteriores, trata sobre la variación continua de funciones de variable real, el cálculo de variaciones se ocupa de la variación de los que se conocen como funcionales.

En términos informales, un funcional es una "función de funciones", es decir, una regla de correspondencia entre el conjunto de las funciones y el de los números reales.

Un ejemplo, muy interesante e ilustrativo de un funcional, es la integral definida de una función de variable real:

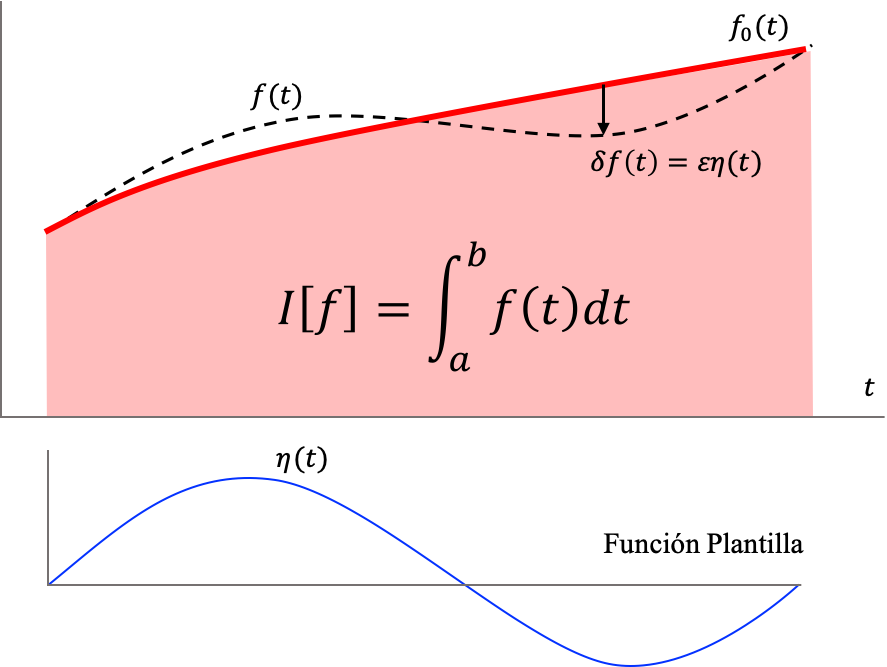
$$ I[f]=\int_a^b f(t)\;\mathrm{d}t $$

La notación $I[f]$, en lugar de $I(b)$ como lo usamos en la Sección Integrales, trata de poner en evidencia el hecho de que lo que nos interesa aquí no es el valor mismo de la integral definida, sino cómo el valor de esta cantidad cambia si modificamos la función $f$. En la Figura (variacion_funcion) se muestra la interpretación gráfica de la integral definida. Sabemos que el área bajo la curva, el valor de nuestro funcional, dependerá de si usamos la función $f(t)$ o $f_0(t)$.

El área bajo una curva es un funcional, en tanto depende de la función que represente la curva, $f(t)$ o $f_0(t)$ Se conoce como una variación $

Figura 4.10. El área bajo una curva es un funcional, en tanto depende de la función que represente la curva, $f(t)$ o $f_0(t)$ Se conoce como una variación $

De la misma manera en la que se puede estudiar el efecto que un cambio muy pequeño $\Delta t$ en el valor de la variable independiente $t$ tiene en una función de variable real $f(t)$, como lo hicimos por ejemplo para definir la derivada (ver la Sección Derivadas), en el cálculo variacional es posible estudiar el efecto que un cambio pequeño $\delta f$ de una función $f$ tiene en el funcional $I[f]$

Para hacerlo debemos primero definir otra función $\eta$ que sirve de "plantilla" para el cambio. Al cambio en $f$ se lo llama variación y se escribe como:

\begin{equation} \label{eq:variacion} \delta f\equiv \epsilon \eta \end{equation}

Una ilustración del concepto de variación se muestra en la Figura (variacion_funcion). Allí reconocemos una importante propiedad de la función de plantilla $\eta(t)$ y es que vale cero en los extremos del intervalo considerado $[a,b]$.

El cálculo variacional surgió originalmente para resolver problemas prácticos en física, tales como hallar las funciones que máximan o minimizan (extremos) funcionales de alguna utilidad.

Así por ejemplo, considere la siguiente pregunta: ¿cuál es la curva más corta que conecta dos puntos en el plano de euclidiano?

Para responder a esta pregunta debemos primero construir el funcional "distancia a lo largo de una curva", también llamado, longitud de arco (Apostol, 1969):

\begin{equation} \label{eq:longitud_curva} I[f]=\int_a^b \sqrt{1+\left|\frac{\mathrm{d}f}{\mathrm{d}t}\right|^2}\;\mathrm{d}t \end{equation}

Queremos encontrar la función $f_0$ tal que $I[f_0]$ tenga el mínimo valor entre todas las posibles funciones $f$.

Para encontrar la función que minimiza este funcional debemos, como se acostumbra en el cálculo (Apostol, 1967), derivar el funcional respecto a la cantidad que parametriza la variación: $\epsilon$.

Escribamos el funcional de forma más general, en términos de una función cercana al mínimo escrita como $f=f_0+\epsilon\eta$:

\begin{equation} \label{eq:funcional_integral} I[f]=\int_a^b L(f(t),\dot{f}(t),t)\;\mathrm{d}t \end{equation}

Nótese que hemos escrito el integrando como una función general $L$ que depende del valor de la función $f(t)$, de su derivada $\dot{f}(t)$ y de la variable independiente $t$. Implícitamente, el funcional depende también del parámetro $\epsilon$ dado que $f=f_0+\epsilon\eta$.

Si derivamos el funcional respecto de $\epsilon$, obtenemos:

$$ \frac{\mathrm{d}I[f]}{\mathrm{d}\epsilon}=\int_a^b \frac{\mathrm{d}}{\mathrm{d}\epsilon} L(f(t),\dot{f}(t),t)\;\mathrm{d}t $$

Aplicando la regla de la cadena, la integral del lado derecho nos queda:

$$ \frac{\mathrm{d}I[f]}{\mathrm{d}\epsilon}=\int_a^b \left( \frac{\partial L}{\partial f}\frac{\mathrm{d}f}{\mathrm{d}\epsilon}+ \frac{\partial L}{\partial \dot{f}}\frac{\mathrm{d}\dot{f}}{\mathrm{d}\epsilon} \right) \;\mathrm{d}t $$

Como $f(t)=f_0(t)+\epsilon\eta(t)$, entonces $\mathrm{d}f/\mathrm{d}\epsilon=\eta$, mientras que $\mathrm{d}\dot{f}/\mathrm{d}\epsilon=\dot{\eta}$. Así la integral anterior se desarrolla como:

\begin{equation} \label{eq:dIdepsilon} \frac{\mathrm{d}I[f]}{\mathrm{d}\epsilon}=\int_a^b \left( \frac{\partial L}{\partial f}\eta+ \frac{\partial L}{\partial \dot{f}}\dot{\eta} \right) \;\mathrm{d}t \end{equation}

El término $\int_a^b (\partial L/\partial \dot{f})\dot{\eta}\;\mathrm{d}t$ se puede integrar por partes, si se hace $u=\partial L/\partial \dot{f}$ y $\mathrm{d}v=\dot{\eta}\;\mathrm{d}t$:

$$ \int_a^b \frac{\partial L}{\partial \dot{f}}\dot{\eta}\;\mathrm{d}t= \left.\frac{\partial L}{\partial \dot{f}}\eta\right|_a^b- \int_a^b \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial L}{\partial \dot{f}}\right)\eta\;\mathrm{d}t $$

El primer término del lado derecho de la ecuación anterior es cero, en tanto, por definición $\eta(a)=\eta(b)=0$.

Reemplazando en la Ec. (dIdepsilon), la derivada del funcional respecto de epsilon queda finalmente:

$$ \frac{\mathrm{d}I[f]}{\mathrm{d}\epsilon}=\int_a^b \eta(x) \left(\frac{\partial L}{\partial f}-\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial L}{\partial \dot{f}}\right) \;\mathrm{d}x $$

Para que $I[f]$ sea mínima en $f=f_0$ su derivada $\mathrm{d}I[f]/{\mathrm{d}\epsilon}$ debe ser cero en $\epsilon=0$. Esto equivale a la ecuación integral:

\begin{equation} \label{eq:ecuacion_integral_variaciones} \int_a^b \eta(x) \left(\frac{\partial L}{\partial f}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{f}}\right) \;\mathrm{d}t=0 \end{equation}

que lamentablemente no es muy útil para resolver nuestro problema original. Para acercarnos a la solución necesitamos de un poderoso teorema:

Proposición: Lema fundamental del cálculo de variacions. Si una función continua $f(t)$ en el intervalo abierto $(a,b)$ satisface la igualdad:

$$ \int_a^b f(t)h(t)\;\mathrm{d}t=0 $$

para toda función $h(t)$ continuamente diferenciable (todas sus derivadas son continuas) y con soporte compacto (acotada), entonces $f(t)=0$.

De acuerdo con este teorema, y suponiendo que $\eta(t)$ es continuamente diferenciable y acotada, la función entre paréntesis la ecuación integral (ecuacion_integral_variaciones) es:

\begin{equation} \label{eq:ecuacion_euler_lagrange} \frac{\partial L}{\partial f}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{f}}=0 \end{equation}

Esta ecuación es una versión particular (para funciones de una sola variable) de la que se conoce en la historia como la ecuación de Euler-Lagrange y que será de importancia central en este libro.

Volviendo a nuestro problema original, es decir, encontrar la curva con la menor longitud entre dos puntos, y reconociendo que:

$$ L(f(t),\dot{f}(t),t)=\sqrt{1+|\dot{f}(t)|^2}, $$

Entonces $\partial L/\partial f=0$ (no aparece el símbolo $f$ en la fórmula de $L$) y $\partial L/\partial\dot{f}=\dot{f}/\sqrt{1+|\dot{f}(t)|^2}$. De allí, la ecuación de Euler-Lagrange (ecuacion_euler_lagrange) en este problema se convierte en:

$$ \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\dot{f}}{\sqrt{1+|\dot{f}(t)|^2}}\right)=0 $$

Esta ecuación significa que el término entre paréntesis es constante. Después de un poco de algebra, la expresión resultante, se puede integrar para obtener:

$$ f(t)=At+B, $$

donde $A$, $B$ son constantes.

La respuesta final a la pregunta original es ahora clara: la curva más corta entre dos puntos en el plano euclidiano es una línea recta.

4.1.9.1. Algoritmos en el cálculo variacional

Si el cálculo variacional es poco común en los textos básicos de cálculo infinitesimal, los algoritmos relacionados con él son aún más escasos en los textos de análisis numérico.

Dada la importancia del cálculo variacional en la mecánica nos detendremos un momento aquí para explorar desde la algoritmia, al menos la solución al problema de cálculo variacional que expusimos en la sección anterior: el cálculo de la curva más corta entre dos puntos en el plano euclidiano.

Para ello escribamos primero la rutina que servirá en nuestro caso como funcional (y que implementa la Ec. longitud_curva):

In [1]:
def funcional_integral(f0,eta,epsilon,a,b,**opciones_de_f0):
    
    #Definimos las función con su variación
    f=lambda t:f0(t,**opciones_de_f0)+epsilon*eta(t)
    
    #La derivada de f la calculamos con derivative
    from scipy.misc import derivative
    dfdt=lambda t:derivative(f,t,0.01)
    
    #Este es el integrando del funcional
    from numpy import sqrt
    L=lambda t:sqrt(1+abs(dfdt(t))**2)
    
    #El funcional es la integral definida del integrando
    from scipy.integrate import quad
    integral=quad(L,a,b)
    longitud=integral[0]
    
    return longitud

Nótese que un funcional en el lenguaje de la algoritmia es una rutina que recibe como parámetros otras rutina (en este caso f0 y eta) y devuelve un valor numérico (en este caso longitud.)

La rutina en el Alg. (funcional_integral), si bien parece compleja, recoje todos los elementos que hemos aprendido en esta sección: los parametros opcionales de una rutina expresados como **opciones_de_f0 y que vimos en una nota de la Sección Funciones, las funciones lambda que vimos en la misma sección, la derivada numérica calculada usando derivative que conocimos en la Sección Derivadas y la integral por cuadraturas usando quad de la Sección Integrales.

Más importante aún es el hecho que esta rutina puede usarse para cualquier funcional que se exprese como una integral definida de la forma de la Ec. (funcional_integral). Para adaptarla a otras situaciones, simplemente se debe cambiar la función L. En la sección de problemas al final de este capítulo se pone a prueba esta rutina en otros contextos.

Supongamos ahora que queremos calcular la curva más corta que une los puntos del plano cartesiano $(0,0)$ y $(\pi,1)$ (es decir $a=0$ y $b=\pi$). Para ello proponemos una función de referencia $f_0(t)=(t/\pi)^n$. Esta función para por ambos puntos para todo $n$. Como función de plantilla $\eta(t)$, que debe ser una función acotada de acuerdo al lema fundamental del cálculo de variaciones, usaremos la función trigonométrica seno (que cumple la condición $\eta(a)=\sin 0=0$ y $\eta(b)=\sin\pi=0$).

El siguiente algoritmo implementa estas elecciones:

In [2]:
#Intevalo entre los puntos
from numpy import pi
a=0
b=pi

#Funcion de referencia
def curva(t,n=1):
    return (t/pi)**n

#Función plantilla
from numpy import sin
eta=sin

Para ilustrar el uso de la rutina en el Alg. (funcional_integral), calculemos la longitud de arco para el caso en el que $n=2$ y $\epsilon=0.5$:

In [3]:
n=2
If=funcional_integral(curva,eta,0.5,a,b,n=n)

I[f] = 3.337162809417341

Para encontrar la trayectoria más corta entre los puntos seleccionados, debemos minimizar una función del tipo longitud_arco(epsilon) que llame a la rutina funcional_integral, pero que solo dependa de la variable que queremos minimizar, es decir de epsilon. Para ello podemos definir la función lambda:

In [5]:
longitud_arco=lambda epsilon:funcional_integral(curva,eta,epsilon,
                                                a,b,n=n)

La minimización, finalmente, se consigue usando la rutina minimize del paquete SciPy, capaz de encontar el mínimo de funciones escalares con un número arbitario de variables. Lo único que necesita minimize para lograr su cometido es que le pasemos una rutina que tenga un solo parametro, en nuestro caso longitud_arco y un valor de prueba para la variable independiente (en nuestro caso usaremos $\epsilon=0$):

In [6]:
from scipy.optimize import minimize
solucion=minimize(longitud_arco,0.0)

Resultado de la minimización:
      fun: 3.2975722013512403
 hess_inv: array([[0.73687233]])
      jac: array([1.1920929e-06])
  message: 'Optimization terminated successfully.'
     nfev: 12
      nit: 3
     njev: 4
   status: 0
  success: True
        x: array([0.25801323])

Nótese que el resultado de la rutina minimize es un objeto entre cuyos atributos se encuentra el valor de la variable independiente x que hace mínima la función de nuestro interés, en este caso longitud_de_arco.

Puesto en términos de nuestro problema el resultado anterior indica que para curvas del tipo $f_0(t)=(t/\pi)^2$, que sufren variaciones con una función plantilla $\eta(t)=\sin t$, la curva de mínima longitud entre el punto $(0,0)$ y el punto $(0,\pi)$, corresponde a una variación con $\epsilon=0.258$.

Hagamos un gráfico de la función resultante y de su comparación con la solución analítica:

In [8]:
%matplotlib inline
In [9]:
import matplotlib.pyplot as plt
plt.figure()

from numpy import linspace,pi
ts=linspace(0,pi)

#Valor de epsilon proveniende de la minimización
epsilon=solucion.x[0]

plt.plot(ts,curva(ts,n=n),'r.',
         label=f"Curva de referencia")
plt.plot(ts,curva(ts,n=n)+epsilon*eta(ts),'b-',
         label=f"Curva variada con $\epsilon$={epsilon:g}")
plt.plot(ts,curva(ts,n=1),'k--',
         label=f"Línea recta")

plt.legend();

#--hide--
plt.xlabel("t");

Figura 4.11. La curva continua indica una aproximación numérica al camino más corto entre los puntos $(0,0)$ y $(0,\pi)$ del plano euclidiano, encontrada al minimizar el funcional longitud de arco y usando como función de prueba $f_0=(t/\pi)^n$ (linea punteada) y como función plantilla $\epsilon(t)=\sin t$. El valor de $\epsilon$ que corresponde a la solución se muestra en la etiqueta. Para comparación se muestra (linea rayada) la solución exacta, que corresponde a una línea recta.

4.1.1. Gráficos interactivos

Para ver los gráficos interactivos use a las libretas de Jupyter que que están disponibles en la versión electrónica del libro.

Figura 4.12.

Indice | Previo: Fundamentos.Calculo.EcuacionesDiferenciales | Siguiente: Fundamentos.Calculo.Series