Indice | Previo: Fundamentos.Conicas.Anomalias | Siguiente: Fundamentos.Conicas.Rotaciones

4.2.15. Área de las cónicas

Existe un último resultado de la geometría analítica de las cónicas que es de interés para la mecánica celeste: el área encerrada por estas curvas. Como veremos en el Capítulo El problema de los dos cuerpos, el área es la única cantidad geométrica cuyo valor puede predicerse de forma exacta como función del tiempo cuando describimos el movimiento de un cuerpo respecto a un centro de atracción.

Un poco de historia: Newton, el área debajo de la hipérbola y la invención del cálculo. El cálculo del área encerrada por curvas arbitrarias (cuadratura) es uno de los problemas clásicos de la geometría y en los 1600 uno de los que motivo la invención del cálculo infinitesimal (ver Sección Integrales.)

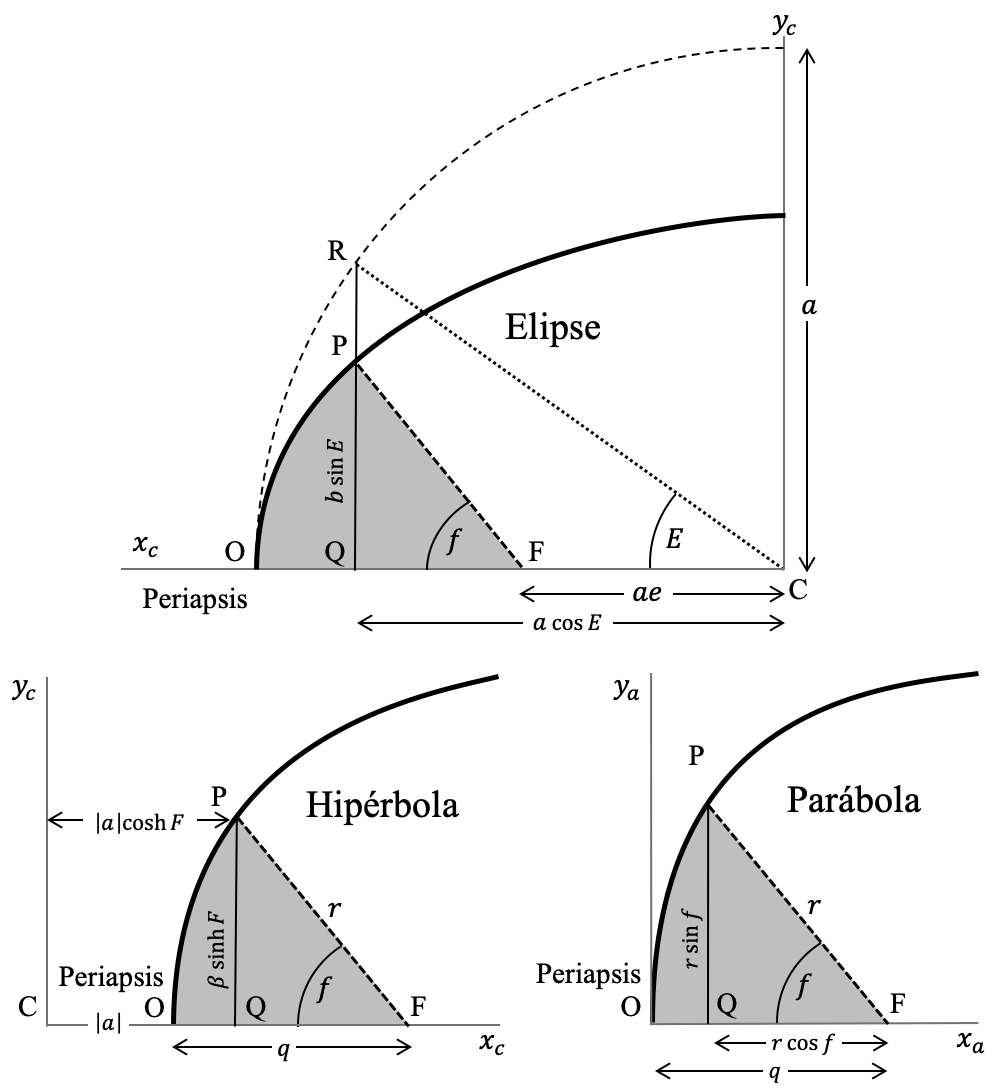
En la Figura (conicas_area) se muestran las construcciones geométricas que usaremos en las próximas sesiones para calcular el área encerrada por elipses, hipérbolas y parábolas en función de las anomalías definidas en las secciones anterioes y otros parámetros geométricos de esas mismas cónicas.

Figura 4.32. Construcción geométrica usada aquí para deducir la relación entre las anomalías $f$, $E$ y $F$ y el área del sector de cónica (región sombreada).

En los tres casos el área del sector de cónica PQF, que es el área de interés para nosotros en la mecánica celeste, se puede siempre escribir como la suma del segmento PQO y del triángulo PFQ:

\begin{equation} \label{eq:area_sector} \Delta A\equiv A_\mathrm{PQF}=A_\mathrm{PFQ}+A_\mathrm{PQO} \end{equation}

El problema, en las tres cónicas consiste en calcular estas dos áreas como función de las anomalías excéntricas (en el caso de la elipse y la hipérbola y de la anomalía verdadera en el caso de la parábola.

4.2.15.1. Área de un sector de elipse

El área del triángulo en PFQ en la elipse (ver panel superior en Figura (conicas_area)) se puede escribir en términos de la anomalía excéntrica $E$ como:

\begin{eqnarray} \nonumber A_\mathrm{PFQ} & = & \frac{1}{2} b\sin E (a\cos E-ae)\\ \label{eq:A_PFQ} & = & \frac{1}{2} ab\sin E\cos E - abe\sin E \end{eqnarray}

Por otro lado, el área del segmento de elipse PQO se puede expresar como la integral definida:

$$ A_\mathrm{PQO}=\int_{-a}^{x_c} y_c(x) \mathrm{d}x $$

Por las propiedades geométricas de la elipse (ver Sección Anomalía de la elipse) la ordenada del punto P es $y_c(x)=(b/a)Y(x)$, donde $Y$ es la correspondiente ordenada del punto R sobre la circunferencia circunscrita en la elipse de radio $a$ . De esta manera el área del segmento de elipse se puede expresar en términos del área de segmento de circulo RQO como:

\begin{equation} \label{eq:A_PQO} A_\mathrm{PQO}=\frac{1}{2}A_\mathrm{RQO} \end{equation}

Por su parte:

$$ A_\mathrm{RQO}=A_\mathrm{RCO}-A_\mathrm{RCQ} $$

que a su vez se escriben en términos de $E$ como:

\begin{equation} \label{eq:A_RQO} A_\mathrm{RQO}=\frac{1}{2}a^2 E-\frac{1}{2}a^2\sin E\cos E \end{equation}

Reemplazando la Ec. (A_RQO) en la (A_PQO) y esta última junto con la Ec. (A_PFQ) en la fórmula original (Ec. area_sector) obetenmos finalmente:

\begin{equation} \label{eq:area_sector_elipse} \Delta A_\mathrm{elipse}=\frac{1}{2}ab(E-\sin E) \end{equation}

Siendo la elipse la única figura cerrada entre las cónicas, es posible calcular el área total encerrada por ella haciendo en la última ecuación $E=2\pi$:

\begin{equation} \label{eq:area_elipse} A_\mathrm{elipse}=\pi ab E \end{equation}

4.2.15.2. Área de un sector de hipérbola

La construcción en la Figura (conicas_areas) permite, en el caso de la hipérbola (ver panel inferior izquierdo) escribir las áreas de interés en la Ec. (area_sector) como:

\begin{eqnarray} \nonumber A_\mathrm{PFQ} & = & \frac{1}{2}\beta\sinh F(|a|+q-|a|\cosh F)\\ \nonumber A_\mathrm{PQO} & = & \int_{|a|}^{|a|\cosh F} \beta\sqrt{\frac{x^2}{a^2}-1}\;\mathrm{d}x \end{eqnarray}

Para la última expresión usamos la ecuación de la hipérbola referida al centro (ver Ec. ecuacion_centro_hiperbola).

Resolviendo la integral (ver problemas al final del capítulo), sumando las dos áreas y teniendo en cuenta que $q=|a|(e-1)$ obtenemos finalmente el área del sector de hipérbola:

\begin{equation} \label{eq:area_sector_hiperbola} \Delta A_\mathrm{hiperbola}=\frac{1}{2}|a|\beta(e\sinh F-F) \end{equation}

4.2.15.3. Área de un sector de parábola

De forma análoga a como lo hicimos con la hipérbola, podemos escribir lás áreas que componen el sector de parábola en términos de la anomalía verdadera $f$ (ver panel inferior derecho en la Figura (conicas_areas)):

\begin{eqnarray} \nonumber A_\mathrm{PFQ} & = & \frac{1}{2}r^2 \sin f\cos f\\ \nonumber A_\mathrm{PQO} & = & \int_{0}^{q-r\cos f} \sqrt{2 p x}\;\mathrm{d}x \end{eqnarray}

donde en la integral hemos usado la ecuación de la parábola con origen en el ápside $y_a(x_a)^2=2px_a$ (ver Ec. ecuacion_apside_pe).

A pesar de que estas expresiones parecen más fáciles de desarrollar matemáticamente, en realidad encontrar una versión simplificada del área del sector de parábola es más complicado de lo que es para el caso del sector de elipse y el de hipérbola.

En términos llanos (sin simplificaciones trigonométricas), el área del sector, que es la suma de las ecuaciones anteriores resulta ser:

$$ \Delta A_\mathrm{parabola}=\frac{1}{2}\frac{p^2\sin f\cos f}{(1+\cos f)^2}+\frac{p^2}{3}\left(\frac{1-\cos f}{1+\cos f}\right)^{3/2} $$

donde hemos usado la ecuación de la parábola en coordenadas cilíndricas, $r=p/(1+\cos f)$ y el hecho que $q=p/2$.

La fracción en el segundo término del lado derecho se puede escribir como:

$$ \frac{1-\cos f}{1+\cos f}=\tan\frac{f}{2} $$

y esto nos ofrece una clave de cómo simplificar el primer término: escribiéndo $\sin f$ y $\cos f$ en términos de $\tan(f/2)$:

\begin{eqnarray} \sin f & = & \frac{2\tan\frac{f}{2}}{1+\tan^2\frac{f}{2}}\\ \cos f & = & \frac{1-\tan^2\frac{f}{2}}{1+\tan^2\frac{f}{2}}\\ \end{eqnarray}

Reemplazando, el área del sector de parábola queda:

$$ \Delta A_\mathrm{parabola}=\frac{1}{4} p^2\tan\frac{f}{2}\left(1-\tan^2\frac{f}{2}\right)+\frac{p^2}{6}\tan^3\frac{f}{2} $$

y simplifando obtenemos finalmente:

\begin{equation} \label{eq:area_sector_parabola} \Delta A_\mathrm{parabola}=\frac{1}{4}p^2\left(\tan\frac{f}{2}+\frac{1}{3}\tan^3\frac{f}{2}\right) \end{equation}

Indice | Previo: Fundamentos.Conicas.Anomalias | Siguiente: Fundamentos.Conicas.Rotaciones