Indice | Previo: Problema3Cuerpos.ConstanteJacobi | Siguiente: Problema3Cuerpos.PotencialModificado
8.11. Las regiones de exclusión¶
Saber que en cualquier instante del movimiento, la posición y velocidad de la partícula de prueba en el CRTBP obedece la ecuación general definida por la cuadratura de Jacobi, puede ser de gran utilidad para determinar cualquier cantidad cinemática conocidas las demás. Así por ejemplo, dado un sistema para el cuál se conoce el valor de la constante de Jacobi $C_J$, la rapidez de la partícula $v$ puede calcularse fácilmente si se específica su posición $\vec r:(x,y,z)$:
\begin{equation} \label{eq:velocidad_constante_jacobi} v^2 = \frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + x^2 + y^2 - C_J \end{equation}Hay una propiedad adicional de esta relación que puede ser explotada para, sin necesidad de resolver la ecuación de movimiento, conocer de antemano los lugares del espacio que puede visitar la partícula. Y es que es claro que cualquiera sea la posición que ella tenga, debe cumplirse que siempre $v^2 \geq 0$. Esta condición física elemental puede expresarse a partir de la Ec. (velocidad_constante_jacobi) mediante la desigualdad:
$$ \frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + x^2 + y^2 - C_J \geq 0 $$Podemos llamar a los puntos del espacio que cumplen esta condición, regiones permitidas del espacio. Aún mejor es identificar todos los puntos que no la cumplen y que forman lo que llamaremos las regiones de exclusión del sistema en el CRTBP, es decir la región en la cuál la partícula nunca estará. Los puntos del espacio que están en las regiones de exclusión satisfacen la desigualdad:
\begin{equation} \label{eq:regiones_exclusion_crtbp} \frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + x^2 + y^2 - C_J < 0 \end{equation}Consideremos varios casos diferentes:
Constante de Jacobi negativa $C_J<0$. Esta situación se produce cuando la velocidad de la partícula es relativamente grande, a saber:
$$ v^2>\frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + (x^2 + y^2) $$
En estas condiciones, todos los términos del lado izquierdo en la desigualdad de la Ec. (regiones_exclusion_crtbp) son positivo definidos. Por tanto, las regiones de exclusión forman un conjunto vacío; es decir ningún punto del espacio esta excluído en el movimiento de la partícula (aunque naturalmente ella no los visitará todos). Podemos comparar esta situación con los sistemas no ligados que estudiamos en el problema de los N cuerpos o con sistemas de excentricidad positiva (energía específica relativa negativa) en el problema de los dos cuerpos.
Constante de Jacobi nula $C_J=0$. Esta situación se producirá cuando, en un momento dado la rapidez de la partícula es:
$$ v^2=v_c^2\equiv\frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + (x^2 + y^2) $$
En estas condiciones de nuevo todos los términos del lado izquierdo en la desigualdad de la Ec. (regiones_exclusion_crtbp) son positivo y otra vez no hay regiones de exclusión. Podemos comparar esta situación con el caso de sistemas de excentricidad nula (trayectorias parabólicas) en el problema de los dos cuerpos.
Constante de Jacobi positiva $C_J=0$. Naturalmente, esta es la situación menos trivial y la que conduce a regiones de exclusión no nulas. Para analizar la geometría de las regiones de exclusión en este caso considere una situación con un valor $C_J$ razonablemente pequeño ($C_J\approx 5-v^2$). Podemos analizar los puntos del espacio considerando estos casos particulares:
a. Puntos cercanos a la partícula 1, $r_1\ll r_2$. Dado que normalmente $\alpha\ll 1$ y por tanto la partícula 1 esta cerca al origen de coordenadas, los puntos que cumplen esta condición satisfacen también que $\rho\equiv\sqrt{x^2+y^2}\ll 1$. En estas condiciones la desigualdad que define las regiones de exclusión será aproximadamente:
$$ \frac{2(1-\alpha)}{r_{1}}< C_J $$
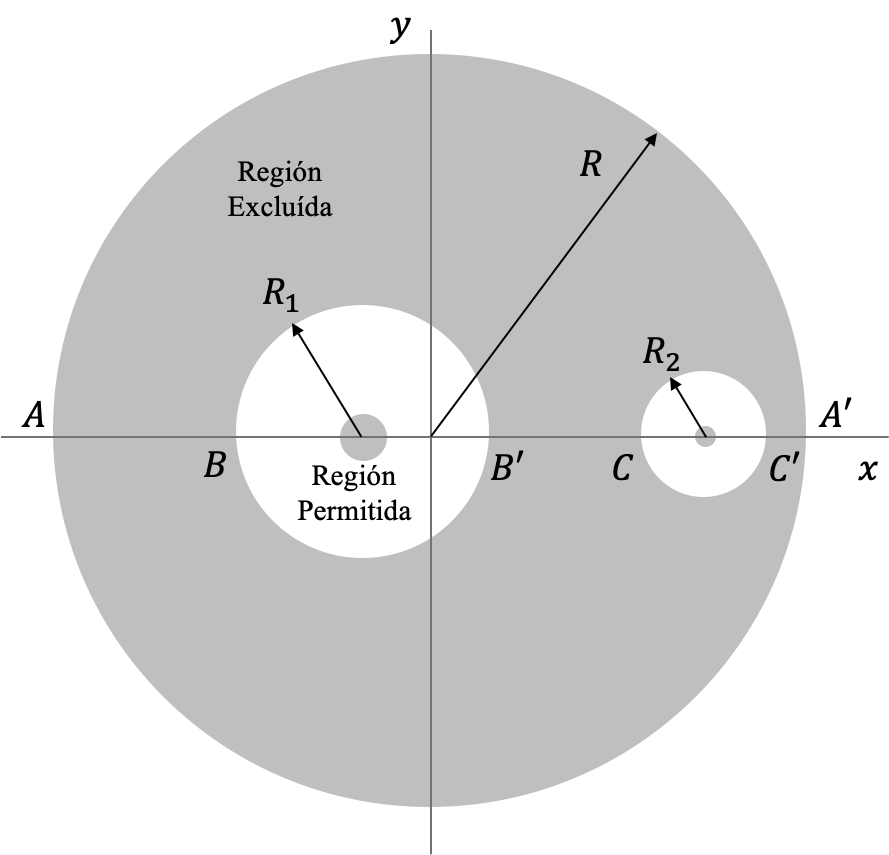
Que equivale a decir que todos los puntos afuera de la esfera $r_1>R_1\equiv2(1-\alpha)/C_J$ están en la región de exclusión (ver Figura (regiones_exclusion_crtbp)).
b. Puntos cercanos a la partícula 2, $r_2\ll r_1$. En este caso $\rho\equiv\sqrt{x^2+y^2}\approx (1-\alpha)$ y la desigualdad que define la región de exclusión se puede excribir como:
$$ r_2>R_2\equiv\frac{2\alpha}{C_J-(1-\alpha)^2} $$
todos los puntos más allá de esta esfera tampoco serán visitados por la partícula.
c. Puntos muy lejanos $r_2,r_1\gg 1$. Las regiones de exclusión definidas por las condiciones anteriores, parecerían excluir a todos los puntos que están más allá de las esferas de radio $R_1$ y $R_2$. Sin embargo a distancias muy grandes, la desigualdad de la Ec. (regiones_exclusion_crtbp) se convierte:
$$ x^2+y^2<C_J $$
que describe el interior de un cilíndro de radio $\sqrt{C_J}$.
En síntesis, para valores regulares de $C_J$ la región de exclusión corresponde a todos los puntos adentro de un cilindro de radio $R=\sqrt{C_J}$, pero afuera de una esfera de radio $R_1=2(1-\alpha)/C_J$ centrada en la primera partícula 1 ($x_1=-\alpha$) y otra de radio $R_2=2\alpha/[C_J-(1-\alpha)^2]$ centrada en la partícula 2 ($x_2=-\alpha$). En la Figura (regiones_exclusion_crtbp) se ilustra esquemativamente la geometría de las regiones de exclusión en esta situación.
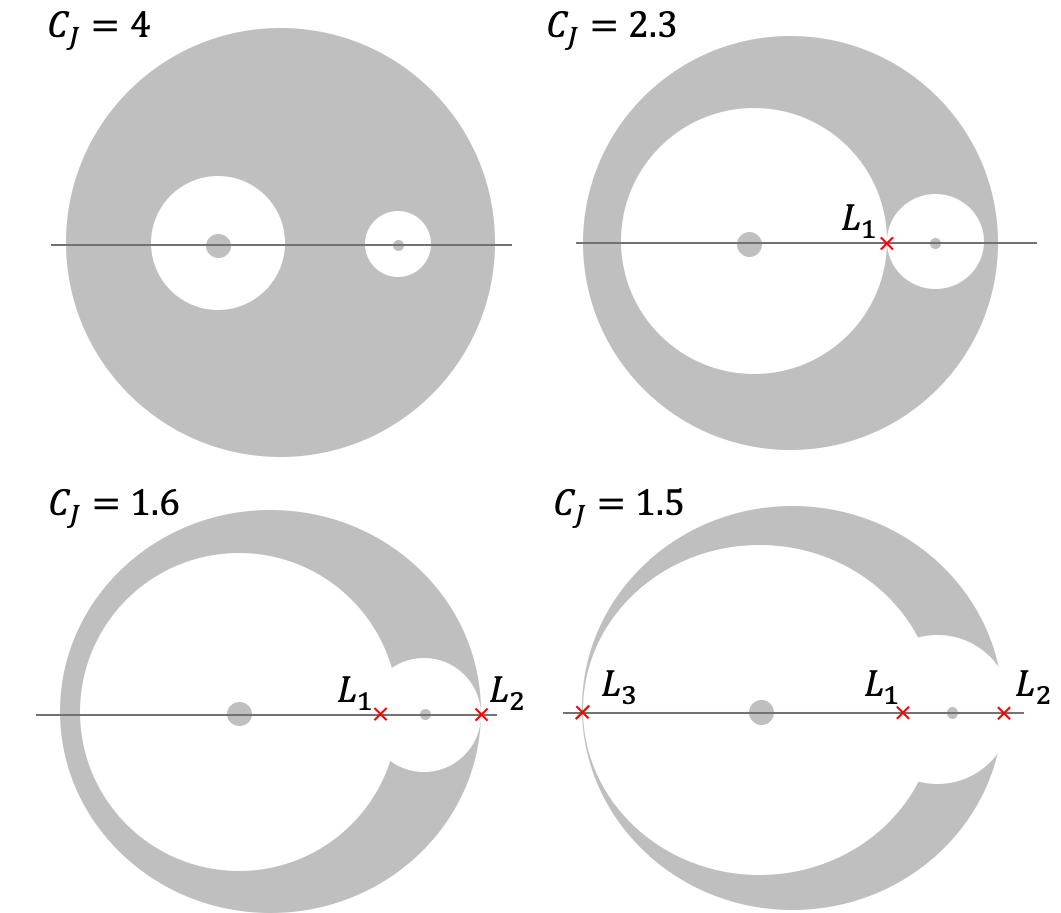
¿Cómo son el tamaño y la geometría de las regiones de exclusión para valores diferentes de $C_J$?. En la Figura (code:limites_regiones_exclusion) se muestra como cambia la posición del intercepto de los límites de las regiones de exclusión (puntos A, A', B, B', C, C' en Figura (regiones_exclusion_crtbp)) al cambiar el valor de la constante de Jacobi.
%matplotlib inline
Como vemos allí entre menor es el valor de la constante de Jacobi, más cerca están la frontera de las regiones permitidas alrededor de las partículas masivas y más pequeño es la regiones de exclusión alrededor de ellas (cilíndro de radio $R$). Para un determinado valor crítico de $C_J$ las regiones permitidas alrededor de las partículas se tocan en un punto (los puntos B' y C coinciden). Llamamos a ese punto (que se encuentra sobre el eje $x$, es decir en $y=z=0$), punto colineal $L_1$ (ver siguiente sección). Para valores aún menores de $C_J$, la región permitida alrededor de la partícula 2 intercepta el límite exterior de la región de exclusión en un punto que llamaremos punto colineal $L_2$. Finalmente, cuando $C_J$ alcanza un tercer valor crítico, la región permitida alrededor de la partícula 1 toca el límite exterior de la región de exclusión en un punto que llamaremos punto colineal $L_3$. En la Figura (definicion_colineales_crtbp) se ilustra esquemáticamente la progresión en el tamaño y geometría de la región de exclusión al cambiar el valor de $C_J$ y la definición y posición de los puntos colineales $L_1$, $L_2$ y $L_3$.
¿Qué es lo que pasa exactamente en los límites de las regiones de exclusión?. De acuerdo con la Ec. (regiones_exclusion_crtbp) estas regiones están limitadas por la condición:
\begin{equation} \label{eq:regiones_exclusion_crtbp2} \frac{2(1-\alpha)}{r_{1}} + \frac{2\alpha}{r_{2}} + x^2 + y^2 - C_J = 0 \end{equation}Esta relación, de acuerdo a la definición misma de $C_J$ (ver Ec. velocidad_constante_jacobi) demuestra que en esos puntos fronterizos, la rapidez de la partícula es siempre nula $v=0$. Llamamos al lugar geométrico que ocupan esos puntos y que forman superficies que tapiza por adentro y por afuera a las regiones de exclusión, superficies de cero velocidad.
Cuando al moverse en una región permitida la partícula llega a las superficies de cero velocidad, se detiene brevemente, antes de emprender nuevamente su camino hacia adentro de la regiones permitida de la que venía. Las superficies de cero velocidad actúan entonces como espejos dinámicos en el CRTBP.
Para ilustrar los conceptos de regiones de exclusión, puntos colineales y superficies de cero velocidad, construyamos un sistema físico real, simulemos su trayectoria y comparemos esa trayectoria con la ubicación esperada de estas regiones del espacio. En el algoritmo a continuación se define el sistema, sus condiciones iniciales y se resuelve numéricamente las ecuaciones de movimiento.
#Propiedades del sistema y condiciones iniciales
alfa=0.3
ro=[0.3,0.0,0.0]
vo=[0.5,0.401,0.0]
#Tiempos de integración
from numpy import linspace
Nt=500
ts=linspace(0,20,Nt)
#Resuelve numéricamente la ecuación de movimiento
from pymcel.export import crtbp_solucion
solucion=crtbp_solucion(alfa,ro,vo,ts)
#Extrae las posiciones y velocidades en el sistema rotante
rs=solucion[0]
vs=solucion[1]
¿Cuál es el valor de la constante de Jacobi de este sistema?. Usemos la rutina constante_jacobi que definimos en la Sección Cuadratura de Jacobi de un sistema simulado para calcularlo:
from pymcel.export import constante_jacobi
CJs=constante_jacobi(alfa,rs,vs)
CJ=CJs[0]
Para encontrar la regiones de exclusión (y las superficies de cero velocidad) para este valor específico de la constante, podemos utilizar el método que usamos en la Sección El valor de la constante de Jacobi, donde construímos una malla coordenada y superficies de contorno para visualizar los valores de la constante de Jacobi. Ahora, nos interesa visualizar, para un valor fijo de $C_J$, el valor predicho para $v^2$ de acuerdo con la Ec. (velocidad_constante_jacobi):
#Tamaño de la malla y número de filas y columnas
rango=2.0
NG=80
#Malla de puntos en el plano
from numpy import meshgrid,linspace,ones_like
X,Y=meshgrid(linspace(-rango,rango,NG),linspace(-rango,rango,NG))
#Valores de v^2
from numpy import sqrt
V2=2*(1-alfa)/sqrt((X+alfa)**2+Y**2)+2*alfa/sqrt((X-1+alfa)**2+Y**2)+X**2+Y**2-CJ
Usando las coordenadas de la partícula y la matriz de rapideces V2, podemos ahora dibujar la relación entre ambas:
fig=plt.figure(figsize=(5,5))
ax=fig.gca()
#Curva de cero velocidad
ax.contour(X,Y,V2,levels=[0],colors='k')
#Región de exclusión
ax.contourf(X,Y,V2,levels=[-100,0],colors='k',alpha=0.3)
#Trayectoria
ax.plot(rs[:,0],rs[:,1],color='green')
#Posición de las partículas con masa
ax.plot([-alfa],[0],'o',color='blue',markersize=10*(1-alfa))
ax.plot([1-alfa],[0],'o',color='orange',markersize=max(2,10*alfa))
#Decoración
ax.set_title(f"Sistema: $\\alpha={alfa}$, $C_J={CJ:g}$")
ax.set_xlim((-rango,rango));
ax.set_ylim((-rango,rango));
Busque las figuras interactivas incluídas en el sitio en línea del libro.
Indice | Previo: Problema3Cuerpos.ConstanteJacobi | Siguiente: Problema3Cuerpos.PotencialModificado