Indice | Previo: Problema3Cuerpos.PotencialModificado | Siguiente: Problema3Cuerpos.Aplicaciones.RadioHill

8.13. Los puntos de equilibrio de Lagrange

Al final de la sección anterior aprendimos que en el CRTBP existen puntos en el espacio alrededor de las partículas masivas en las que si se deja en reposo una partícula de prueba, esta permanecera allí en equilibrio (para siempre en reposo). Usando gráficos del potencial modificado (que es el que determina la aceleración que sufre una partícula de prueba en reposo) podemos determinar aproximadamente la ubicación de esos "puntos de equilibrio". Pero ¿cuál es su ubicación exacta? ¿qué importancia pueden llegar a tener estos puntos?

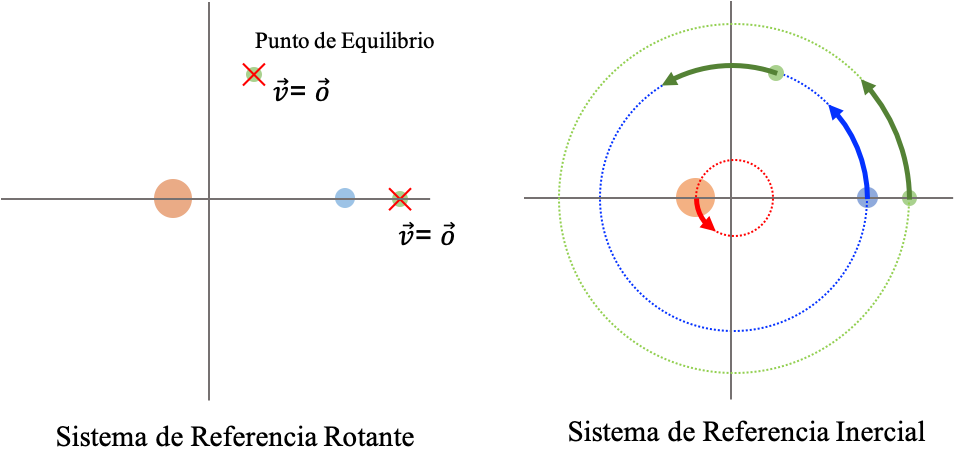
Nota: Equilibrio en el CRTBP. Es importante recordar que cuando hablamos de equilibrio en el contexto del CRTBP, nos referimos a una situación de reposo permanente en el marco de referencia rotante del sistema. Ahora bien, reposo en un sistema rotante, no implica reposo absoluto para cualquier otro sistema de referencia, en especial para el sistema de referencia inercial en el centro de masa. Es obvio que en este último sistema, una partícula de prueba que está cerca a partículas masivas no puede permanecer quieta. La atracción gravitacional de ellas induce algún tipo de movimiento.

El reposo permanente en el sistema rotante implica naturalmente que en el sistema inercial del centro de masa la partícula se mueve en una trayectoria circular, con exactamente la misma velocidad angular del sistema rotante. En otros términos, la partícula de prueba que esta en equilibrio en el CRTBP, simplemente mantiene su posición relativa con respecto a las partículas masivas (no se acerca, ni se aleja), que obviamente están en movimiento. En la Figura (reposo_crtbp) se ilustra esquemáticamente esta importante condición que es fuente de muchas confusiones a la hora de entender las consecuencias prácticas de la dinámica del CRTBP.

Ilustración esquemática de lo que significa que una partícula de prueba este en equilibrio en el sistema rotante del CRTBP. Cuando una partícula tiene velocidad cero y esta en uno de los puntos de equilibrio del sistema, la partícula permanecerá en reposo allí. Sin embargo en el sistema inercial, en realidad, la partícula se mueve siguiendo una trayectoria circular con la misma velocidad angular relativa de las partículas masivas, manteniendo respecto a ella la misma distancia. Equilibrio en el CRTBP no significa reposo en el sistema de referencia inercial.

Figura 8.124. Ilustración esquemática de lo que significa que una partícula de prueba este en equilibrio en el sistema rotante del CRTBP. Cuando una partícula tiene velocidad cero y esta en uno de los puntos de equilibrio del sistema, la partícula permanecerá en reposo allí. Sin embargo en el sistema inercial, en realidad, la partícula se mueve siguiendo una trayectoria circular con la misma velocidad angular relativa de las partículas masivas, manteniendo respecto a ella la misma distancia. Equilibrio en el CRTBP no significa reposo en el sistema de referencia inercial.

De acuerdo con la Ec. (edm_crtbp_reposo) la condición de equilibrio ($\vec v=\vec o$ y $\ddot{\vec{r}}=\vec o$ se puede expresar matemáticamente en términos del potencial modificado como:

$$ \vec \nabla V_\mathrm{mod}=\vec o $$

o en términos explícitos como las tres condiciones:

\begin{eqnarray} \nonumber \frac{\partial V_\mathrm{mod}}{\partial x} & = & 0\\ \nonumber \frac{\partial V_\mathrm{mod}}{\partial y} & = & 0\\ \nonumber \frac{\partial V_\mathrm{mod}}{\partial z} & = & 0 \end{eqnarray}

La condición $\partial V_{mod}/\partial z=0$ implica que:

$$ \frac{\partial V_\mathrm{mod}}{\partial z} = (1-\alpha)\frac{z}{r^3_{1}} + \alpha \frac{z}{r^3_{2}} $$

que solo es válida (para valores finitos de $x,y,z$) si $z=0$. Esta condición implica que todos los puntos de equilibrio del sistema se encuentran sobre el plano xy.

Por otro lado $\partial V_{mod}/\partial y=0$ implica que:

$$ \frac{\partial V_{mod}}{\partial y} = (1-\alpha)\frac{y}{r^3_{1}} + \alpha \frac{y}{r^3_{2}} - y $$

Esta condición produce dos familias de puntos:

  1. Aquellos para los cuáles $y=0$. Llamamos a estos los puntos de equilibrio colineales y como intuirán coinciden con los mismos puntos que descubrimienos estudiando las regiones de exclusión.

  2. Aquellos puntos (no colineales, $y\neq 0$) para los cuáles se cumple que: $$ \frac{1-\alpha}{r^3_{1}} + \frac{\alpha}{r^3_{2}} - 1 = 0 $$

Para saber el número y ubicación exacta de estas dos familias de puntos es necesario, finalmente, aplicar la condición $\partial V_{mod}/\partial x=0$:

\begin{equation} \label{eq:dVmod_dx_cero} (1-\alpha)\frac{(x-x_1)}{r^3_{1}} + \alpha \frac{(x - x_2)}{r^3_{2}} - x = 0 \end{equation}

8.13.1. Puntos de equilibrio triangulares

La ubicación de los puntos que se encuentran fuera del eje x puede hayarse resolviendo simultáneamente las ecuaciones:

\begin{eqnarray} \nonumber \frac{1-\alpha}{r^3_{1}} + \frac{\alpha}{r^3_{2}} - 1 & = & 0 \\ \nonumber \displaystyle (1-\alpha)\frac{(x-x_1)}{r^3_{1}} + \alpha \frac{(x - x_2)}{r^3_{2}} - x & = & 0 \end{eqnarray}

Si multiplicamos ambas ecuaciones por $(x - x_2)$ y $(x - x_1)$, respectivamente, y primero restamos y luego sumamos las expresiones resultantes, obtenemos este conjunto de ecuaciones equivalente en las cuáles se ha eliminado $x$:

\begin{eqnarray} \nonumber -x_2 + \frac{(1-\alpha)}{r^3_{1}}(-x_1+x_2) &= 0 \\ \nonumber -x_1 + \frac{\alpha}{r^3_{2}}(-x_2+x_1) &= 0 \end{eqnarray}

Teniendo en cuenta que $x_1 = -\alpha$ y $x_2 = 1-\alpha$, la solución independiente de las dos ecuaciones produce:

$$ r_{1} = r_{2} = 1 $$

Es decir, los puntos de equilibrio por fuera del eje $x$ están a la misma distancia, tanto de la partícula 1 como de la partícula 2; distancia que además es igual a la distancia entre esas partículas (recordemos que en las unidades canónicas del CRTBP, $a=1$).

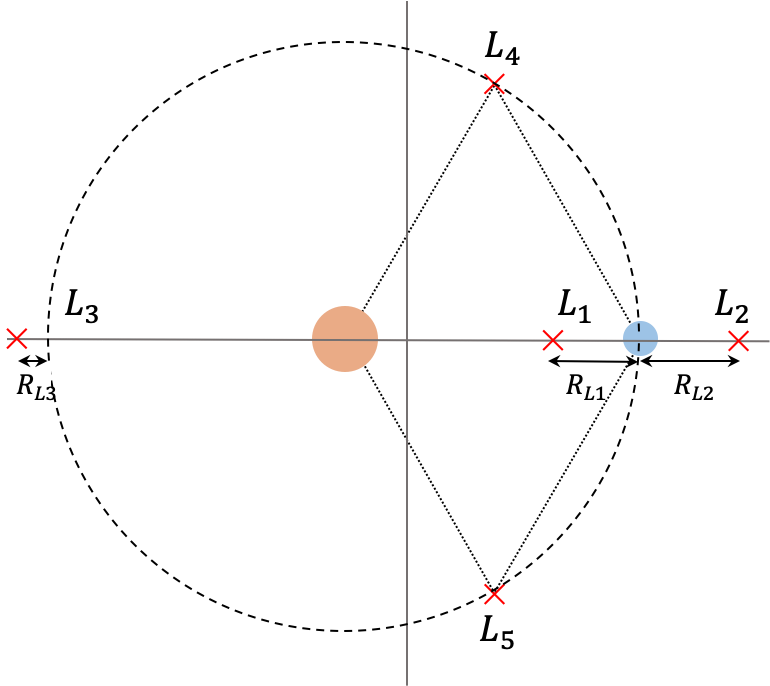
Sólo hay dos puntos en el plano $x-y$ que satisfacen esta condición: uno que tiene $y>0$ y que llamaremos $L_4$ (por encontrarse en la misma dirección del movimiento de las partículas masivas en el sistema inercial) y un segundo punto que tiene $y<0$ y que llamaremos $L_5$. En la Figura (horizontal_puntos_equilibrio_crtbp) se ilustra esquemáticamente la ubicación de estos puntos.

Ubicación esquemática de los puntos de equilibrio de Lagrange: puntos colineales $L_1$, $L_2$ y $L_3$ y puntos triangulares $L_4$ y $L_5$. Para los puntos colineales se han indicado las distancias $R_{L1}$, $R_{L2}$ y $R_{L3}$ de cada uno a un punto de referencia vecino: la segunda partícula en el caso de $L_1$ y $L_2$ o el lado opuesto de una circunferencia imaginaria centrada en la partícula más masiva y con radio unitario (círcunferencia rayada). Es importante entender que la circunferencia imaginaria representada aquí no es en general la trayectoria de la partícula 2 que debería estar centrada en el origen (centro de masa) y solo coincide con ella en el caso en que $

Figura 8.125. Ubicación esquemática de los puntos de equilibrio de Lagrange: puntos colineales $L_1$, $L_2$ y $L_3$ y puntos triangulares $L_4$ y $L_5$. Para los puntos colineales se han indicado las distancias $R_{L1}$, $R_{L2}$ y $R_{L3}$ de cada uno a un punto de referencia vecino: la segunda partícula en el caso de $L_1$ y $L_2$ o el lado opuesto de una circunferencia imaginaria centrada en la partícula más masiva y con radio unitario (círcunferencia rayada). Es importante entender que la circunferencia imaginaria representada aquí no es en general la trayectoria de la partícula 2 que debería estar centrada en el origen (centro de masa) y solo coincide con ella en el caso en que $

8.13.2. Puntos de equilibrio colineales

Partiendo de la Ec. (dVmod_dx_cero) y recordando que los puntos de equilibrio colineales tienen $y = z = 0$, la coordenada $x$ de estos puntos satisface la ecuación algebraica:

\begin{equation} \label{eq:puntos_colineales_condicion_x} f_L(x)\equiv x - (1-\alpha)\frac{(x-x_1)}{|x - x_1|^3} - \alpha \frac{(x - x_2)}{|x - x_2|^3} = 0 \end{equation}

La siguiente rutina implementa el cálculo de la función $f_L(x)$ en el lado izquierdo de la ecuación anterior:

In [1]:
def funcion_puntos_colineales(x,alfa):
    x1=-alfa
    x2=1-alfa
    f=(1-alfa)*(x-x1)/abs(x-x1)**3+alfa*(x-x2)/abs(x-x2)**3-x
    return f
In [2]:
%matplotlib inline

Figura 8.126.

En la Figura (code:crtbp_puntos_colineales_ecuacion) se muestra un gráfico de esta función, que corresponde a un conjunto de polinomios de grado 5, que intersectan el eje $x$ en al menos tres puntos (los puntos colineales).

8.13.3. Punto colineal de equilibrio, $L_1$

Este punto se encuentra en el intervalo $x_1<x<x_2$. Por la misma razón se cumple que $(x-x_1)>0$ y $(x-x_2)<0$ y por tanto, la Ec. (puntos_colineales_condicion_x) se escribirá como:

$$ x - \frac{(1-\alpha)}{(x - x_1)^2} + \frac{\alpha}{(x_2 - x)^2} = 0 $$

Si llamamos $R_{L1}\equiv x_2-x$ (distancia de $L_1$ a la partícula 2, ver Figura (horizontal_puntos_equilibrio_crtbp)) y escribimos explícitamente $x_1=-\alpha$ y $x_2=1-\alpha$, la ecuación se puede escribir en la forma:

$$ (1-\alpha-R_{L1}) - \frac{(1-\alpha)}{(1-R_{L1})^2} + \frac{\alpha}{R_{L1}^2} = 0 $$

Una aproximación útil se puede obtener para valores pequeños de $\alpha\ll 1$, para los cuáles también asumimos que $R_{L1}\ll 1$. Si se expande el segundo término de la ecuación anterior usando el teorema del binomio, el resultado se puede escribir como:

$$ (1-\alpha-R_{L1})R_{L1}^2 - (1-\alpha)(1+2R_{L1})R_{L1}^2 + \alpha \approx 0 $$

Con un poco de álgebra podemos despejar $R_{L1}$ como:

$$ R_{L1}^3 \approx \frac{\alpha}{3-2\alpha} $$

Dado que $\alpha\ll 1$, podemos usar nuevamente el teorema del binomio para simplificar aún mas esta expresión eliminando todos los términos de segundo orden en $\alpha$ del lado derecho. La expresión aproximada más simple para $R_{L1}$ será:

\begin{equation} \label{eq:L1_aprox} R_{L1}\approx\sqrt[3]{\frac{\alpha}{3}} \end{equation}

Con estas aproximaciones, la coordenada $x$ del punto $L_1$ se puede escribir finalmente como:

\begin{equation} \label{eq:xL1_aprox} x_{L1}\approx1-\alpha-\sqrt[3]{\frac{\alpha}{3}} \end{equation}

Más adelante evaluaremos la calidad de esta aproximación, comparándola con el valor preciso de esta cantidad, calculado resolviendo numéricamente la Ec. (puntos_colineales_condicion_x).

8.13.4. Punto colineal de equilibrio, $L_2$

Este punto se encuentra en el intervalo $x_1,x_2<x$, en el que ambos $(x-x_1)$ y $(x-x_2)$ son positivos y por tanto la Ec. (puntos_colineales_condicion_x) se puede escribir como:

$$ x - \frac{(1-\alpha)}{(x - x_1)^2} - \frac{\alpha}{(x - x_2)^2} = 0 $$

Si ahora llamamos $R_{L2}\equiv x-x_2$, la ecuación resultante es:

$$ (1-\alpha+R_{L2}) - \frac{(1-\alpha)}{(1+R_{L2})^2} - \frac{\alpha}{R_{L2}^2} = 0 $$

Aplicando un procedimiento análogo al que usamos para encontrar $R_{L1}$, obtenemos también:

$$ R_{L2}\approx\sqrt[3]{\frac{\alpha}{3}} $$

es decir, para $\alpha\ll 1$, el punto de equilibrio colineal $L_2$ e encuentra, aproximadamente a la misma distancia de la partícula 2 que el punto $L_1$. Esta propiedad puede ser usada para definir algunas cantidades de interés astronómico sobre las que volveremos más adelante.

Finalmente la coordenada $x$ de $L_2$ se puede finalmente escribir como:

\begin{equation} \label{eq:xL2_aprox} x_{L2}\approx1-\alpha+\sqrt[3]{\frac{\alpha}{3}} \end{equation}

8.13.5. Punto colineal de equilibrio, $L_3$

Este punto se encuentra en el intervalo $x<x_1,x_2$ en el que ambos $(x-x_1)$ y $(x-x_2)$ son negativos y por tanto la Ec. (puntos_colineales_condicion_x) queda:

$$ x + \frac{(1-\alpha)}{(x_1 - x)^2} + \frac{\alpha}{(x_2 - x)^2} = 0 $$

Si ahora hacemos $R_{L3}\equiv -1-x$ (ver Figura (horizontal_puntos_equilibrio_crtbp)), la ecuación queda:

$$ (R_{L3}-1) + \frac{(1-\alpha)}{(-\alpha+R_{L3}+1)^2} + \frac{\alpha}{(1-\alpha +1+R_{L3})^2} = 0 $$

Expandiendo el segundo y tercer término usando el teorema del binomio, la ecuación aproximada a primer orden en $R_{L3}-\alpha$ será:

$$ -R_{L3}-1 + (1-\alpha)[1-2(R_{L3}-\alpha)] + \frac{\alpha}{4}[1-(R_{L3}-\alpha)]\approx 0 $$

Despejando $R_{L3}$ obtenemos:

$$ R_{L3}\approx\frac{5\alpha-7\alpha^2}{12-7\alpha} $$

y usando nuevamente el teorema del binomio para expresar la solución a primer orden en $\alpha$, obtenemos finalmente la aproximación:

$$ R_{L3}\approx\frac{5\alpha}{12} $$

La coordenada $x$ del punto colineal $L_3$ se puede finalmente escribir como:

\begin{equation} \label{eq:xL3_aprox} x_{L3}\approx -1-\frac{5\alpha}{12} \end{equation}

8.13.6. Precisión de la aproximación analítica

La posición precisa de los puntos colineales de Lagrange se puede encontrar, para cualquier valor de $\alpha$, resolviendo numéricamente la Ec. (puntos_colineales_condicion_x). Para ello necesitamos usar un algoritmos que permita encontrar la raíz de una ecuación dado un íntervalo en el que sabemos se encuentra esa misma raíz (que en el caso de cada punto de Lagrange será diferente). El método de bisección (o cualquier método de horquillado) será ideal para este propósito.

Así por ejemplo, la posición de $L_1$ ($x_{L1}$), para el valor de $\alpha$ considerado en la puntos_colineales_condicion_x(crtbp_puntos_colineales_ecuacion), se obtiene usando el siguiente algoritmo:

In [4]:
alfa=0.3
from scipy.optimize import bisect
x_L1_num=bisect(funcion_puntos_colineales,0,1-1.01*alfa,args=(alfa,))

Posición precisa de L1 (alfa = 0.3) = 0.28612978205071515

Nótese que hemos utilizado como intervalo de horquillado, aquel que se encuentra entre el centro de masa (origen de coordenadas) y un punto cercano (pero no igual para evitar las singularidades de la ecuación) a la posición de la partícula 2. La elección adecuada de este intervalo es crucial.

Podemos comparar el valor preciso calculado para la posición del punto $L_1$, con la aproximación obtenida con la Ec. (L1_aprox):

In [6]:
x_L1_aprox=1-alfa-(alfa/3)**(1./3)

Posición aproximada de L1 (alfa = 0.3) = 0.23584111663872204

Naturalmente hay una discrepancia importante debido a que ciertamente, en este caso, $\alpha$ no es muy pequeña. En la Figura (code:crtbp_colineal_aproximacion) se compara la posición relativa ($R_{L1}$, $R_{L2}$ y $R_{L3}$) de los puntos colineales de Lagrange, calculada de forma precisa (resolviendo numéricamente la Ec. puntos_colineales_condicion_x) y usando las expresiones aproximadas desarrolladas en esta sección, para un amplio rango de valores del parámetro $\alpha$.

In [8]:
#Valores de alfa
from numpy import log10,logspace
log_alfas=linspace(log10(1e-4),log10(4e-1),100)

#Calcula posición relativa de los puntos
Ls=[]
for log_alfa in log_alfas:
    from scipy.optimize import bisect
    alfa=10**log_alfa
    Ls+=[[
        #Valores precisos
        (1-alfa)-bisect(funcion_puntos_colineales,0,1-2*alfa,args=(alfa,)),
        bisect(funcion_puntos_colineales,1-0.5*alfa,2,args=(alfa,))-(1-alfa),
        -1-bisect(funcion_puntos_colineales,-2,-0.5,args=(alfa,)),
        #Valores aproximados
        (alfa/3)**(1./3),
        (alfa/3)**(1./3),
        5*alfa/12
    ]]
from numpy import array,abs
Ls=array(Ls)

#Grafica
fig,axs=plt.subplots(3,1,figsize=(4,6),sharex=True)
ax=axs[0]
ax.plot(10**log_alfas,Ls[:,0],'k-',label='Preciso')
ax.plot(10**log_alfas,Ls[:,3],'k--',label='Aproximado',lw=3)
ax=axs[1]
ax.plot(10**log_alfas,Ls[:,1],'k-')
ax.plot(10**log_alfas,Ls[:,4],'k--',lw=3)
ax=axs[2]
ax.plot(10**log_alfas,Ls[:,2],'k-')
ax.plot(10**log_alfas,Ls[:,5],'k--',lw=3)

#Decora
axs[2].set_xlabel("$\\alpha$")
axs[0].set_ylabel("$R_{L1}$")
axs[1].set_ylabel("$R_{L2}$")
axs[2].set_ylabel("$R_{L3}$")
axs[0].legend()
for ax in axs:
    ax.set_xscale("log");
    ax.grid()
fig.tight_layout()

Figura 8.127. Distancia relativa de los puntos de equilibrio colineales en el CRTBP para un amplio rango de valores de $\alpha$.

Como puede verse de la Figura, la posición de los puntos de equilibrio colineales $L_1$ y $L_2$ puede obtenerse con errores menores a $\sim 1\%$ para valores de $\alpha<10^{-2}$ (una situación bastante común en astronomía). Se nota además que el punto $L_2$ esta siempre más lejos de la partícula 2 que el punto $L_1$ (la curva rayada en los gráficos de ambas cantidades es igual). De otro lado, la aproximación analítica para la posición del punto $L_3$ es bastante precisa para un amplio rango de valores de $\alpha$.

Indice | Previo: Problema3Cuerpos.PotencialModificado | Siguiente: Problema3Cuerpos.Aplicaciones.RadioHill