9.9. Problemas seleccionados¶
- Libertad del Lagrangiano. Sea $L(\{q\},\{\dot{q}\},t)$ un Lagrangiano para un sistema con $n$ variables generalizadas $(q_{1},q_{2},\dots,q_{n})$ que satisface las ecuaciones de Lagrange. Muestre por sustitución directa que
$$L'(\{q\},\{\dot{q}\},t)=L(\{q\},\{\dot{q}\},t)+\frac{{\rm d}}{{\rm d}t}F(\{q\},t)$$también satisface las ecuaciones de Lagrange, donde $F$ es cualquier función diferenciable respecto a sus argumentos.
- Transformaciones puntuales. Sea $L(\{q\},\{\dot{q}\},t)$ un Lagrangiano para un sistema con $n$ variables generalizadas $(q_{1},q_{2},\dots,q_{n})$ que satisface las ecuaciones de Lagrange. Suponga que se hace una transformación puntual, es decir, a otro conjunto de coordenadas independientes $s_{1},...,s_{n}$ por medio de las siguientes ecuaciones
$$q_{l}=q_{l}(s_{1},\dots,s_{l},t),\qquad l=1,\dots,n.$$Muestre que si el Lagrangiano se expresa como función de $s_{j}$, $\dot{s}_{j}$ y $t$ a través de las ecuaciones de transformación puntual, entonces $L$ satisface las ecuaciones de Lagrange con respecto a las nuevas coordenadas $s$,
$$ \frac{{\rm d}}{{\rm d}t}\left(\frac{\partial L}{\partial\dot{s}_{j}}\right)-\frac{\partial L}{\partial s_{j}}=0. $$En otras palabras, muestre que las ecuaciones de Lagrange son invariantes (su forma matemática no cambia) bajo las llamadas transformaciones puntuales.
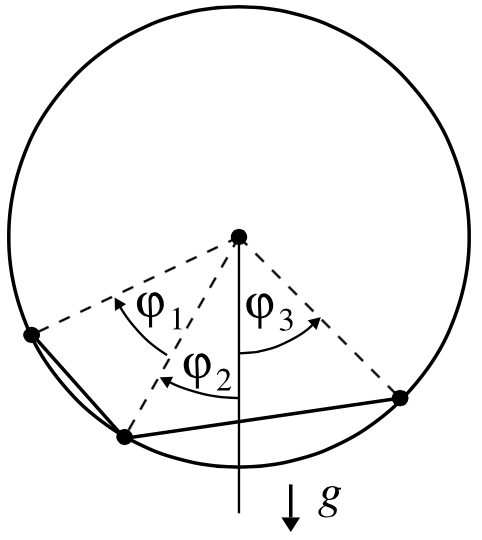
- Ligaduras. Tres masitas puntuales $m_1$, $m_2$ y $m_3$ se fijan a los extremos de dos barras sin masa y se deslizan sin fricción en un aro circular de radio $R$, que permanece vertical en el campo gravitacional de la Tierra.
$a$) ¿Cuántas ligaduras tiene el sistema? Escriba las ecuaciones de ligadura (restricciones) del sistema.
$b$) ¿Cuántos grados de libertad tiene el sistema? ¿Cuántas variables generalizadas hacen falta para describir el sistema? Defina el conjunto de coordenadas generalizadas independientes que va a usar para definir el Sistema
$c$) Encuentre la función Lagrangiana para este sistema.
$d$) Escriba las ecuaciones de movimiento.
$e$) Encuentre la posición de equilibrio del sistema y la frecuencia de pequeñas oscilaciones alrededor de esa posición.
- Partícula en campo electromagnético. De los resultados básicos de la teoría electromagnética se sabe que una partícula de masa $m$ moviéndose con velocidad $\vec{v}$ respecto a un campo electromagnético, puede describirse mediante el siguiente lagrangiano
$$L=\frac{1}{2}mv^{2}-q\phi+q\vec{A}\cdot\vec{v},$$donde los campos eléctrico $\vec{E}$ y magnético $\vec{B}$ pueden derivarse a partir de los campos $\phi$ (el potencial escalar) y $\vec{A}$ (el potencial vectorial) como
\begin{eqnarray} \vec{E}&=&-\nabla\phi-\frac{\partial\vec{A}}{\partial t}\\\vec{B}&=&\nabla\times\vec{A}. \end{eqnarray}Encuentre las ecuaciones de Euler-Lagrange para la partícula. Hágalo para una sola coordenada generalizada ($x$, por ejemplo) y generalice el resultado a tres dimensiones. Evidentemente, deberá obtener las ecuaciones de Lorentz.
- Función de disipación de Rayleigh. Cuando se estudia el movimiento de un cuerpo en un medio resistivo, la fricción suele modelarse como una función que depende linealmente de la velocidad del objeto relativa al medio. Siendo la fricción una fuerza no conservativa, es claro que no puede derivarse de un potencial escalar dependiente de la posición. Aún así, es posible derivarla a través de la función de disipación de Rayleigh
$$ {\cal F}=\frac{1}{2}\sum_{l=1}^{N}k\left(\dot{x}_{l}^{2}+\dot{y}_{l}^{2}+\dot{z}_{l}^{2}\right), $$donde la suma se hace sobre las $N$ partículas del sistema y $k$ es una constante que depende entre otras cosas de la geometría del objeto. Entonces la fuerza de fricción sobre la $i-$ésima partícula se escribe como
$$\vec{F}_{f}^{i}=\nabla_{v}^{i}{\cal F}.$$Debe notarse que en la expresión anterior, el operador gradiente actúa sobre las velocidades, no sobre las posiciones como es usual con las fuerzas conservativas. Cuando fuerzas derivables de una función de disipación como la de Rayleigh están presentes, las ecuaciones de Euler-Lagrange se escriben así
$$\frac{{\rm d}}{{\rm d}t}\left(\frac{\partial L}{\partial\dot{q}_{j}}\right)-\frac{\partial L}{\partial q_{j}}=-\frac{\partial{\cal F}}{\partial\dot{q}_{j}},$$donde la energía potencial presente en el Lagrangiano contiene aquellos potenciales dependientes de las posiciones y también puede contener aquellos que dependen de las velocidades.
a. Obtenga la ecuación de movimiento para una partícula cayendo verticalmente y desde el reposo bajo la influencia de la gravedad y de una fuerza de fricción derivable de una función de disipación de la forma $kv^{2}/2$.
b. Integre la ecuación para obtener la velocidad como una función del tiempo y muestre que en el límite cuando $t\rightarrow\infty$ la velocidad de la partícula toma un valor constante igual a $mg/k$.
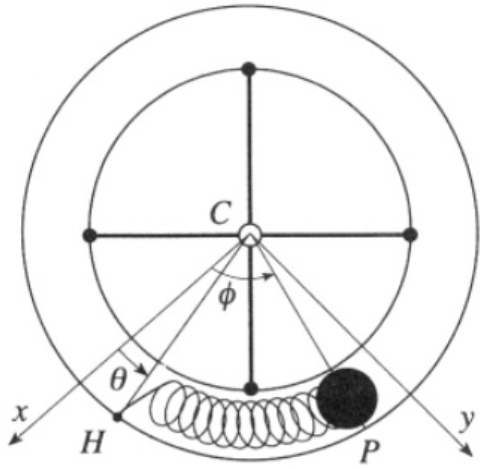
- Partícula en un aro hueco rotante. Un tubo cilíndrico delgado y hueco es doblado para formar un anillo circular hueco de masa $m$ y radio $R$. El anillo está atado por medio de un par de radios sin masa a un eje vertical alrededor del cuál puede rotar sin fricción sobre un plano horizontal. Dentro del anillo, un objeto puntual $P$ de masa $m$ (con la misma masa del anillo) es libre de moverse sin fricción pero en todo momento está conectada a un punto $H$ de el anillo por medio de un resorte sin masa que ejerce sobre $P$ una fuerza restitutiva de magnitud $k\Delta s$ donde $\Delta s$ es la longitud del arco $HP$. Tome a las variables generalizadas como los ángulos $\theta$ y $\phi$ definidas como se muestra en la figura. Desprecie los efectos de la gravedad.
$a$) Escriba el lagrangiano del sistema en función de las variables $\xi=\left(\phi+\theta\right)/\sqrt{2}$ y $\eta=\left(\phi-\theta\right)/\sqrt{2}$.
$b$) Derive las ecuaciones de movimiento para $\xi$ y $\eta$.
$c$) Integre las ecuaciones de movimiento (para $\xi$ y $\eta$) para las siguientes condiciones iniciales: en $t=0$, $\theta=-\pi/4$, $\phi=\pi/4$ y $\dot{\theta}=\dot{\phi}=0$.
$d$) Finalmente, escriba la solución de las variables originales $\theta(t)$ y $\phi(t)$.
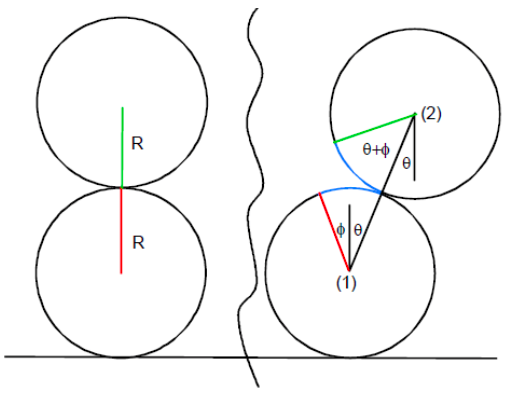
- Cilindros no deslizantes. Un cilindro sólido de radio $R$ descansa sobre otro igual que a su vez se apoya sobre el suelo en equilibrio inestable.
Si el sistema se perturba levemente y no hay deslizamiento entre las superficies de contacto, demuestre que mientras los cilindros permanecen en contacto el ángulo $\theta$ que forma la línea que une los centros con la vertical satisface
$$\dot{\theta}^2=\frac{12g(1-\cos\theta)}{R(17+4\cos\theta-4\cos^2\theta)}$$
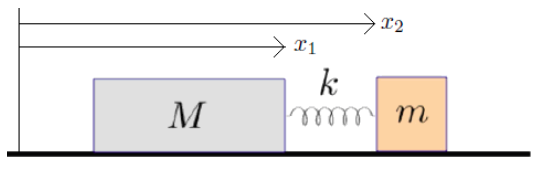
- Bloques unidos por un resorte. Dos bloques están conectados por un resorte de constante elástica $k$ y están libres de moverse sobre una superficie horizontal sin fricción. La longitud natural del resorte es $a$.
$a$) Escriba el lagrangiano del sistema y obtenga la ecuación de movimiento de cada bloque.
$b$) Encuentre las cantidades conservadas del sistema.
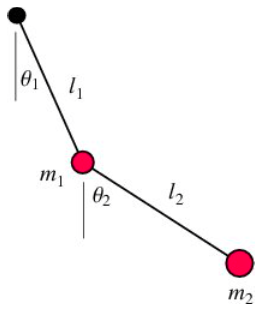
- El péndulo doble. Considere el sistema de dos masas $m_1$ y $m_2$ unidas por dos barras sin masa de longitudes $l_1$ y $l_2$ como se muestra.
\begin{eqnarray} l_{1}&=&0.5\mbox{ m}\\l_{2}&=&1.0\mbox{ m}\\m_{1}&=&1.5\mbox{ kg}\\m_{2}&=&1.0\mbox{ kg}\\\theta_{1}\left(0\right)&=&1.3\frac{\pi}{2}\mbox{ rad}\\\theta_{2}\left(0\right)&=&\dot\theta_{1}\left(0\right)=\dot\theta_{2}\left(0\right)=0 \end{eqnarray}a. Encuentre las ecuaciones de movimiento.
b. Soluciónelas numéricamente y realice una animación que simule el movimiento del sistema para las condiciones:
$c$) Grafique $\dot\theta_1(t)$.
$d$) Vuelva a solucionar las ecuaciones de movimiento cambiando únicamente $\theta_{1}\left(0\right)=1.3\frac{\pi}{2}+0.01\mbox{ rad}$.
$d$) Vuelva a graficar $\dot\theta_1(t)$ y compare con la gráfica anterior. Discuta.
- Cicloide. Una partícula de masa $m$ y carga eléctrica $e$ se mueve en un campo electrostático uniforme cuyo potencial es $\varphi=Ex_1$ y un campo magnético uniforme cuyo potencial vectorial es $\vec{A}=Bx_1\hat{j}$, donde $E$ y $B$ son constantes.
a. Escriba el lagrangiano y muestre que el movimiento es a lo largo de cicloides; más específicamente, que es un movimiento circular uniforme en el plano $xy$ superpuesto por un movimiento con velocidad constante $\vec{v}$ en el plano $yz$.
b. Escriba la rapidez angular $\omega$ del movimiento circular y la componente $v_y$ del movimiento lineal, ambos en términos de las condiciones iniciales.
c. Asuma el la componente $v_z=0$. Encuentre condiciones ideales para los siguientes tres casos:
i. La partícula a veces se mueve en la dirección opuesta a $\vec{v}$.
i. La partícula ocasionalmente está en reposo.
iii. La partícula nunca se mueve en la dirección opuesta a $\vec{v}$.
iv. Grafique los tres tipos de trayectorias del inciso anterior.
e. Encuentre las condiciones iniciales para las cuales la parte circular del movimiento se elimina, por lo que la partícula se moverá con velocidad constante en el plano $yz$. Compruebe que esto sí sucede mediante una gráfica de la situación.
- Órbitas elípticas. Muestre que para movimiento elíptico, con semieje $a$ y excentricidad $e$ en un potencial gravitacional de la forma $-k/r$, la velocidad radial puede ser escrita como
$$ \dot{r}=\frac{\omega a}{r}\sqrt{a^{2}e^{2}-\left(r-a\right)^{2}}, $$donde ${\displaystyle \omega=\left(\frac{k}{m_{r}a^{3}}\right)^{1/2}}$