Indice | Previo: FormalismoHamiltoniano | Siguiente: FormalismoHamiltoniano.EcuacionesCanonicas
10.1. Motivación¶
Como hemos visto en el Capítulo anterior, el formalismo Lagrangiano ofrece innegables ventajas teóricas sobre el formalismo vectorial de la mecánica. Las cantidades implicadas son todas funciones escalares, normalmente más fáciles de manipular. Las fuerzas de restricción, que son difíciles de modelar resultan excluídas desde la descripción misma del sistema. Las constantes de movimiento pueden obtenerse pueden obtenerse a partir de simples consideraciones de simetría. Y por último, pero no menos importante, las ecuaciones de movimiento pueden obtenerse a partir de un principio geométrico (el Principio de Hamilton) lo que le otorga al formalismo una elegancia y belleza matemática superior a la del formalismo vectorial.
Sin embargo, en términos prácticos, el formalismo Lagrangiano todavía adolece de algunas limitaciones. Así por ejemplo, lagrangianos incluso muy sencillos pueden conducir a ecuaciones de movimiento intratables, tanto analítica, como numéricamente. En los sistemas de ejemplo descritos a continuación, ofrecemos un vistazo a las limitaciones del formalismo lagrangiano que justamente justifican la búsqueda de un nuevo formalismo en el que estas limitaciones puedan superarse. Ese nuevo formalismo es justamente el formalismo Hamiltoniano del que nos ocuparemos en este capítulo.
10.1.1. El problema de las ecuaciones de movimiento¶
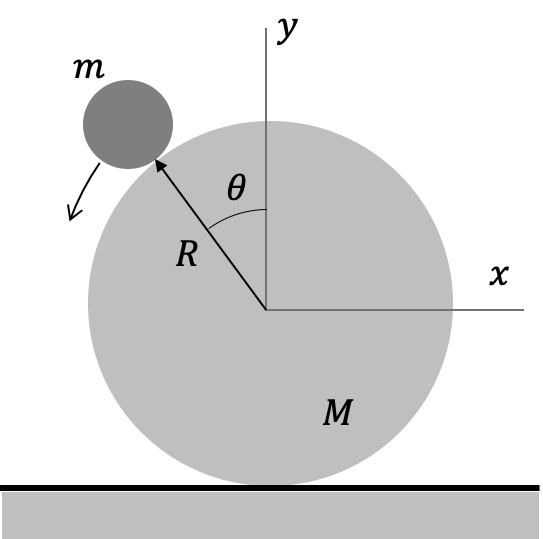
Considere el sistema mostrado en la Figura (hamiltoniano_sistema_simple). En él, una partícula de masa $m$ (partícula 1) puede rodar sin fricción sobre una esfera de masa $M$ y radio $R$ (partícula 2) que a su vez esta sobre una superficie horizontal dura sin fricción (es decir, puede deslizar sobre esa superficie).
El sistema tiene 2 grados de libertad (6 coordenadas cartesians, 2 restricciones sobre la partícula 1 - movimiento sobre la esfera y movimiento en el plano del papel y 2 restricciones para la partícula 1 - movimiento en el plano y movimiento sobre el piso). Lsa variables generalizadas más convenientes para describir la dinámica del sistema son la posición angular $\theta$ de la partícula 1 sobre el partícula 2 y la coordenada $x$ de la partícula 2.
En términos de estas variables generalizadas, las coordenadas cartesianas de la partícula 1 se pueden escribir como:
$$ \begin{array}{rcl} x_1 & = & x-R\sin\theta\\ y_1 & = & R\cos\theta \end{array} $$Usando esta transformación el Lagrangiano del sistema resulta ser (ver Problemas al final del capítulo):
$$ L_\mathrm{EE}=\frac{1}{2}M\dot x^2+\frac{1}{2}m(\dot x^2+R^2\dot\theta^2-2R\dot x\dot\theta\cos\theta)-mgR\cos\theta $$Reemplazando en las Ecuaciones de Euler Lagrange, podemos deducir las ecuaciones de movimiento del sistema como:
$$ \begin{array}{rcl} (M+m)\ddot x - mR\cos\theta\ddot\theta+mR\sin\theta\dot\theta & = & 0\\ r\ddot\theta-\ddot x\cos\theta-g\sin\theta & = & 0 \end{array} $$¿Cuál es la solución a este sistema de ecuaciones?. Ciertamente la simplicidad mecánica del sistema original no se compara con la complejidad matemática de las ecuaciones de movimiento resultantes. Podría uno pensar que siempre es posible apelar a una solución numérica. Para esto último, sin embargo y como hemos mostrado a través de este libro, es necesario primero linearizar las ecuaciones de movimiento. Para hacerlo normalmente introducimos variables del tipo $v_x=\dot x$, $v_\theta=\dot\theta$ y despejamos las primeras derivadas de estas variables. En este caso sin embargo, las derivadas de las variables generalizadas están tan fuertemente acopladas que los despejes necesarios para escribir un conjunto de ecuaciones que sean fáciles de implementar como algoritmos no son tareas triviales.
La búsqueda de simetrías y cuadraturas no parece tampoco sencilla. No hay variables cíclicas, ni simetrías traslacional o rotacional. A lo sumo podemos asegurar que la energía se conserva, de la que podríamos deducir al menos una cuadratura. En síntesis, incluso un sistema mecánico tan sencillo, usando el poderoso formalismo lagrangiano, parece lejos de poder resolverse.
10.1.2. Degeneración del espacio de configuración¶
Hay una propiedad más sutil que muestra la inconveniencia de los dos formalismos de la mecánica estudiados hasta aquí, el formalismo vectorial y el formalismo lagrangiano. Este inconveniente tiene que ver con una propiedad de los espacios geométricos sobre los que se definen las cantidades relavantes en ambos formalismos. En el formalismo vectorial la dinámica se describe sobre el espacio de coordenadas (el espacio físico). En el formalismo lagrangiano la dinámica esta referida al espacio de configuración (el espacio de las variables generalizadas).
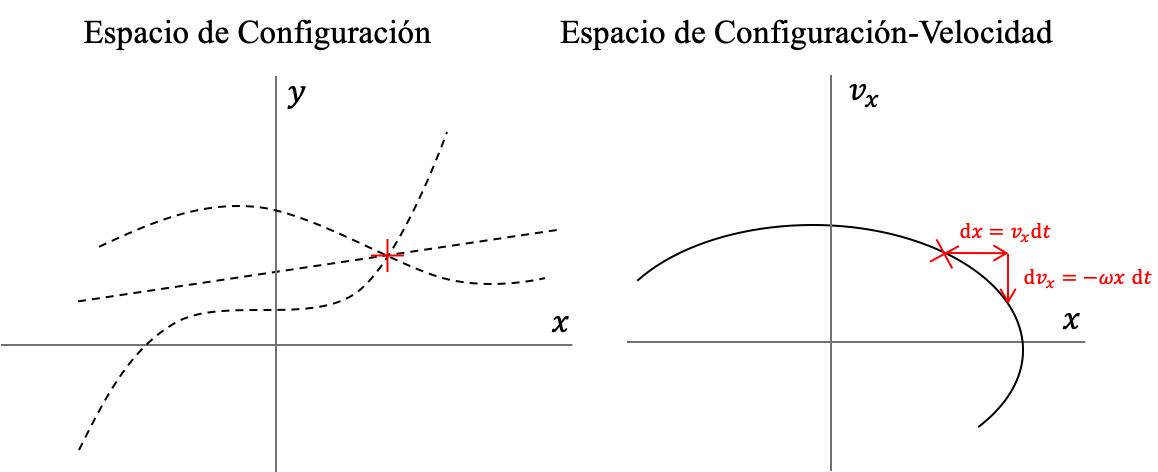
En ambos formalismo, un punto en el espacio correspondiente (ver panel izquierdo de la Figura (espacio_configuracion_fase)) representa tan solo una configuración posible del sistema, pero no su estado de movimiento completo. Es decir, si no se específica la velocidad del sistema en el punto en cuestion y no se proveen las fuerzas o el Lagrangiano del sistema, por ese mismo punto del espacio coordenado o del espacio de configuración, pasan en principio infinitas trayectorias posibles. Llamamos a este problema la degeneración del espacio de configuración.
Es interesante anotar que la razón por la cuál los sistemas dinámicos en el formalismo vectorial y en el formalismo Lagrangiano tienen esta característica, reside justamente en el hecho de que en ambos casos el movimiento es descrito por ecuaciones diferenciales de segundo orden (el postulado de fuerzas de Newton o las ecuaciones de Euler-Lagrange). Sabemos que para resolver este tipo de ecuaciones es necesario específicar no solamente la "posición" inicial del sistema (su configuración) sino también la "velocidad" incial del mismo. La degeneración geométrica del espacio de configuración tiene pues un origen matemático.
Existen soluciones ingeniosas para este problema. Considere por ejemplo el caso de un sistema formado por una partícula unida a un resorte y que se puede mover en virtud de sus restricciones solo en una dirección (un grado de libertad). Tanto en el formalismo vectorial como en el formalismo lagrangiano la ecuación de movimiento del cuerpo es simplemente:
\begin{equation} \ddot x+\omega^2 x = 0 \label{eq:eom_mas} \end{equation}Como explicamos hace un momento el hecho que esta ecuación sea de segundo grado hace que con solo especificar la posición de la partícula en el espacio de configuración (conocer el valor de $x$) no sea posible saber hacia dónde se mueve la partícula; esto incluso sabiendo la aceleración que es provista justamente por la ecuación de movimiento.
Si introducimos ahora la variable auxiliar $v_x=\dot x$, la ecuación de segundo orden anterior es equivalente al sistema de ecuaciones de primer orden dado a continuación:
\begin{equation} \label{eq:edm_mas_linearizado} \begin{array}{rcl} \dot x & = & v_x\\ \dot v_x & = & - \omega^2 x\\ \end{array} \end{equation}Si ahora, en lugar de usar el espacio de configuración, describimos la dinámica en un espacio geométrico nuevo, bidimensional, cuyas coordenadas son $x$ y $v_x$ (al que podemos llamar espacio configuración-velocidad), la dinámica se hace mucho más sencilla (ver panel a la derecha en la Figura (espacio_configuracion_fase)). Nótese que en este espacio por cada punto pasa una y solo una trayectoria (una vez se han especificado los parámetros del sistema). Esto es así porque la variación instantánea de cada una de las coordenadas, dada por el sistema de ecuaciones diferenciales en las Ecs. (edm_mas_linearizado) depende solamente de las coordenadas mismas del punto.
¿Podrá una construcción geométrica como la que hicimos aquí en el caso de un oscilador armónico, generalizarse para cualquier sistema dinámico? ¿será posible construir un espacio generalizado que combine información sobre la configuración y las velocidades generalizadas de modo que la dinámica no este degenerada?. Esta es justamente una de las ideas en el corazón del formalismo Hamiltoniano que introduciremos en este capítulo.
Indice | Previo: FormalismoHamiltoniano | Siguiente: FormalismoHamiltoniano.EcuacionesCanonicas