Indice | Previo: Fundamentos.Calculo.Series | Siguiente: Fundamentos.Conicas.Algebra
4.2. Curvas cónicas¶
En el año 1609, Johannes Kepler descubrió uno de los secretos mejor guardados del Universo: el camino que seguía el planeta Marte alrededor del Sol no era un círculo, como lo "mandaban" siglos de tradición filósofica y astronómica, sino una elipse.
Durante meses el astrónomo Prusiano había estado luchando, sin mucha suerte, por ajustar las precisas observaciones del astrónomo Danés Tycho Brahe ("tico braja") del planeta en cuestión, al modelo que Nicolás Copernico había desarrollado unos 60 años antes y en el que se suponía que los planetas se movían "alrededor" del Sol sobre trayectorias circulares descentradas (el Sol no ocupaba realmente el centro en el sistema Copernicano.)
Después de muchos intentos fallidos Kepler relata, en la que hoy se considera su obra cumbre "Astronomía Nueva", que desesperado empezó a considerar la posibilidad de que la órbita de Marte fuera "ovalada" (con forma de huevo) en lugar de circular. Finalmente, después de muchos intentos, Kepler "adivinó" que el ovalo no podía ser otra cosa sino una elipse, una figura geométrica que había sido ampliamente estudiada por los geómetras de la antigüedad y la edad media, pero cuyo papel en la astronomía no había sido considerado hasta ese momento.
Esta historia marco el inició de la mecánica celeste y el renacimiento del interés astronómico por la elipse y las curvas emparentadas con ella y que hoy llamamos curvas cónicas. En las próximas sesiones repasaremos las propiedades geométricas de las cónicas, desde su definición original hasta su descripción algebraica moderna, en preparación para su aplicación en el estudio de la trayectoria de los cuerpos en mecánica celeste.
4.2.1. Definición geométrica¶
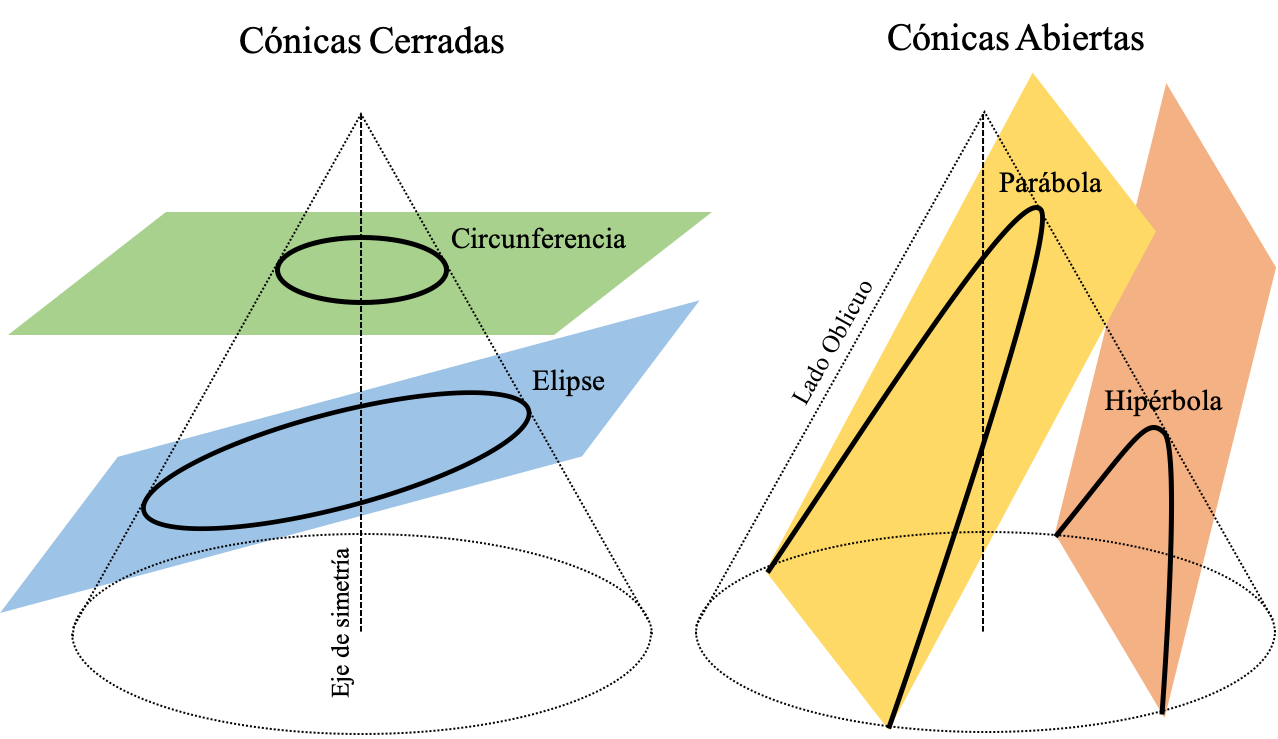
Desde los primeros trabajos geométricos griegos, compilados y organizados por Euclides de Alejandría (323 a 283 a.e.c.) en su libro "Elementos", se sabe que la familia de curvas que resultan de intersectar un plano con un cono (una figura que se forma al hacer rotar en el espacio un triángulo alrededor de uno de sus lados, ver Figura (conica_definicion)) tienen propiedades geométricas especiales. Es a esta familia curvas a las que llamamos cónicas, en clara referencia a su definición geométrica original.
La circunferencia, que es una cónica, resulta por ejemplo de intersectar el cono con un plano perpendicular a su eje de simetría. Si el plano, sin embargo, forma un ángulo distinto de 90 grados con el eje de simetría, pero no es paralelo a los lados del cono, la figura resultante, que es también cerrada como la circunferencia, se llama una elipse. Si el plano es paralelo a los lados oblicuos del cono la figura resultante es abierta y la llamamos una parábola. Finalmente, si el plano no es paralelo a los lados del cono, pero por su ángulo nunca intersecta el eje de simetría, decimos que la figura que se forma es una hipérbola.
4.2.2. Del nombre al álgebra¶
La palabra "parábola" viene del griego $\pi\alpha\rho\alpha\beta\alpha\lambda\lambda\epsilon\iota\nu$ ("parabalei") que significa "poner al lado", "igualar", "comparar" (de allí que una parábola en español sea también una historia que donde se narran hechos que pueden servir como modelos de comportamiento.) Este curioso nombre tiene su origen en la manera como este tipo de curva fue definida de forma más rigurosa a como lo hicimos en la sección anterior, por uno de los más grandes matemáticos de la antiguedad, Apolonio de Perga (ca. 262 a ca. 190 a.e.c.) en su tratado clásico Conicas.
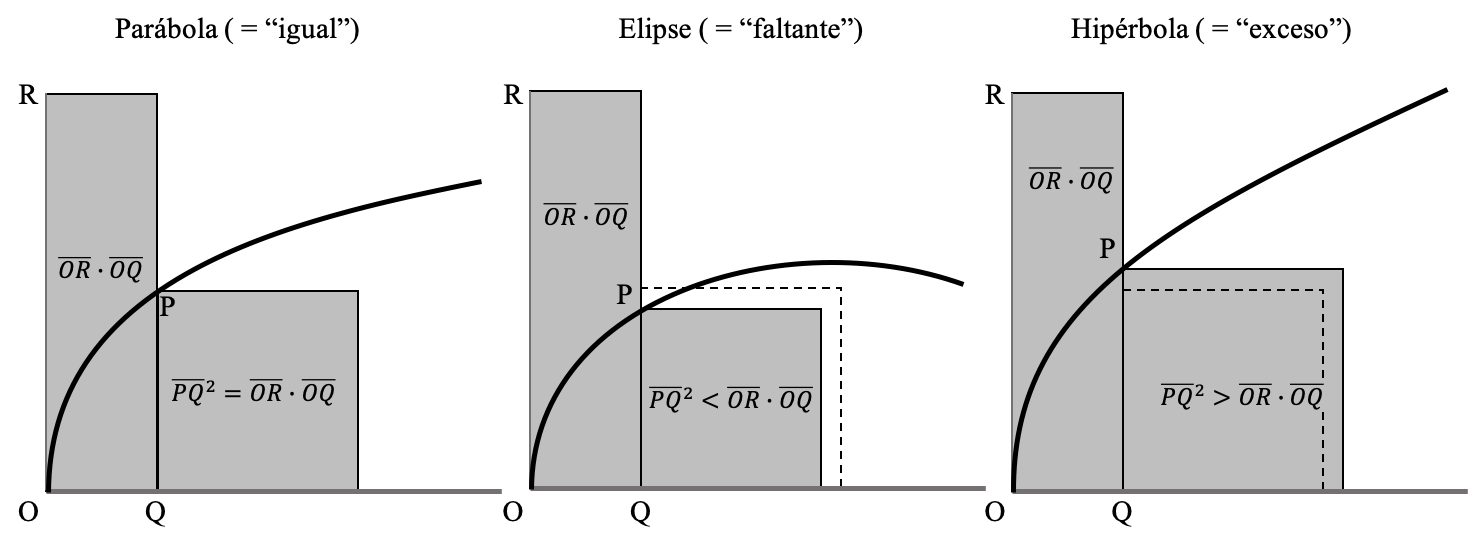
En la Figura (conicas_apolonio) se ilustra la construcción de Apolonio y la razón para el nombre que dió a cada cónica. Para ello ubicamos las curvas sobre el plano de modo que su eje de simetría quede alineado con una semirrecta horizontal que comienza en el punto O que llamaremos apside de la cónica (la elipse tiene dos apsides.) Todas las cónicas de la figura tienen asociado un parámetro que define su tamaño y que es igual a la longitud de un segmento $\overline{\mathrm{OR}}$ perpendicular al eje de simetría. Si aumentamos o disminuímos la longitud de este segmento las cónicas serán más grandes o más pequeñas de las representadas en la figura. Por cada punto P de las cónicas existe un punto Q que es su proyección sobre el eje de simetría.
La propiedad descubierta por Apolonio (y posiblemente por Euclides y otros matemáticos anteriores a él) es que el área del rectángulo que tiene como base el segmento $\overline{\mathrm{OQ}}$ y como altura el parámetro de tamaño, es decir, la longitud del segmento $\overline{\mathrm{OR}}$ puede ser (dependiendo de la cónica) igual, menor o mayor al área del cuadrado que tiene como lado la longitud del segmento $\overline{\mathrm{PQ}}$. En la geometría clásica a esta operación se la llama la aplicación de un rectángulo o la cuadratura del rectángulo.
La parábola es entonces la figura en la que esas áreas son exactamente iguales. De allí su nombre en griego. Por otra parte la elipse, cuyo nombre viene del griego $\epsilon\lambda\epsilon\iota\pi\epsilon\iota\nu$ ("eleipeín") que significa "faltante", es tal que el área del cuadrado no alcanza a ser igual a la del rectángulo. Y en la hipérbola, cuyo nombre viene del griego $\nu\pi\epsilon\rho\beta\alpha\lambda\lambda\epsilon\iota\nu$ ("hiperbalein") que significa "exceso", el área del cuadrado supera la del rectángulo aplicado.
En términos algebraicos (geometría analítica), si construímos un sistema de coordenadas cartesianas con origen en el ápside O, eje $x_a$ (el subíndice indica precisamente que el origen esta en al apside) en la dirección del eje de simetría y eje $y_a$ en dirección del semgento $\overline{\mathrm{OR}}$ (cuya longitud llamamremos $L$), las coordenadas $(x_a,y_a)$ de los puntos sobre las cónicas se relacionan de acuerdo con (Eves, 1972):
\begin{equation} \label{eq:ecuacion_apside} y_a^2 = Lx_a+\eta x_a^2 \end{equation}Aquí $\eta$ es un parámetro que define la "forma" de la cónica, siendo:
- $\eta=0$ en el caso de un parábola.
- $\eta<0$ en el caso de una elipse.
- $\eta>0$ en el caso de una hipérbola.
Por su origen llamaremos a $\eta$ el parámetro de Apolonio de la cónica.
En el algoritmo a continuación usamos estas definiciones para dibujar las cónicas y ver el efecto que tienen los parámetros $L$ y $\eta$ en su tamaño y forma.
#Definimos el algoritmo como una rutina
def conicas_apolonio(eta=-0.5):
#Escala
L=10.0
#Forma
eta=float(eta)
#Máximo valor de x
xamax=L/abs(eta) if abs(eta)>0 else L
#Valores de x en los que graficaremos
from numpy import sqrt,linspace
xas=linspace(0,xamax,100)
#Ecuaciones de las cónicas referidas al apside
from numpy import append
yas_par=sqrt(L*xas)
yas=sqrt(L*xas+float(eta)*xas**2)
#Gráfica
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(6,6))
ax=fig.gca()
ax.plot(xas,yas_par,'k--')
ax.plot(xas,-yas_par,'k--')
ax.plot(xas,yas,'b')
ax.plot(xas,-yas,'b')
#Decoración
ax.grid()
ax.set_title(f"Cónica con $L = {L}$, $\eta={eta}$")
#Fijamos la misma escala en los ejes
from pymcel.plot import fija_ejes_proporcionales
valores=(xas,yas_par,-yas_par,yas,-yas),
fija_ejes_proporcionales(ax,valores,
xmin=-xamax/2,ycm=0);
#Invocamos la rutina
conicas_apolonio()
Trate de demostrar usando el algoritmo o manipulando la Ec. (ecuacion_apside) que la circunferencia, que en la definición original se considera una cónica más, no es más que una elipse para la cuál el parámetro de forma $\eta$ es igual a -1.
Para ver esta una versión interactiva de esta figura por favor use las libretas disponibles en la versión electrónica del libro.
4.2.3. Directriz de las cónicas¶
La definición de Apolonio de las cónicas provista en la sección anterior, no solo nos permite introducir la primera fórmula algebraica para describirlas (Ec. conicas_apolonio) y tal vez la primera en la historia que lo hizo, sino que además nos ayudó a entender el origen de sus nombres.
Sin embargo, esta definición adolece de algunas características que nos resultaran muy útiles en lo sucesivo. No es claro, por ejemplo, la relación entre los parámetros de tamaño $L$ y forma $\eta$ con otras propiedades de la cónica (en el caso de una elipse por ejemplo con su diámetro.)
Una definición más conveniente es la de Arquímedes (introducida posiblemente unos años antes que Apolonio y usada más frecuentemente en la edad media y tiempos modernos.) Esta definición se basa en proporciones más que en áreas.
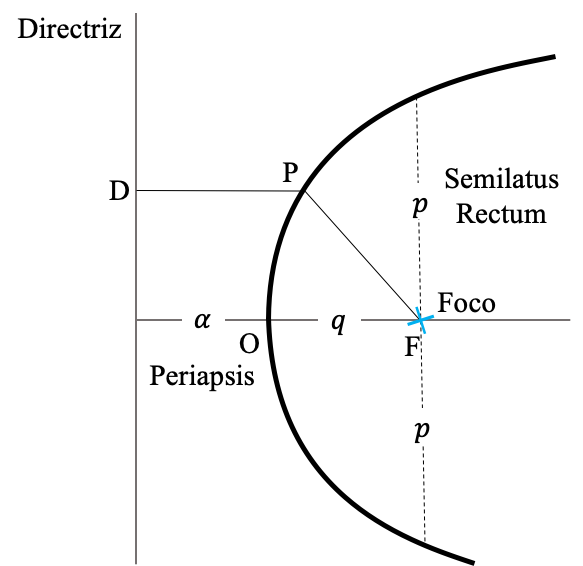
Según esta definición, toda cónica se puede construir partiendo de una recta a la que se llama recta directriz y un punto o foco (ver Figura (conicas_directriz).) Las cónicas son el lugar geométrico de los puntos tal que la razón de la distancia del punto al foco y la distancia del punto a la directriz es constante:
\begin{equation} \label{eq:conica_razon} \displaystyle \frac{\overline{PF}}{\overline{PD}}\equiv e \end{equation}donde $e>0$. A este parámetro lo llamamos la excentricidad de la cónica.
Si definimos un sistema de coordenadas tal que el eje $y_d$ pase por la recta directríz (el subíndice $d$ indica que el sistema de coordenadas esta precisamente referido a la directriz) y el eje $x_d$ por el foco, en términos de las coordenadas $(x_d,y_d)$ de cada punto de la cónica, la condición en la Ec. (conica_razon) se puede escribir como:
\begin{equation} \label{eq:conica_razon_cartesianas} \frac{\sqrt{(F-x_d)^2+y_d^2}}{x_d}=e \end{equation}donde $F$ es la distancia del Foco a la directriz.
Despejando $y$ obtenemos:
\begin{equation} \label{eq:ecuacion_directriz} y_d^2=(e^2-1) x_d^2 + 2F x_d - F^2 \end{equation}Una comparación de esta ecuación con la Ec. (ecuacion_apside) revela inmediatamente que el valor de la excentricidad dependerá de la cónica así:
- $e=1$ en el caso de la parábola.
- $0<e<1$ en el caso de de una elipse.
- $e>1$ en el caso de una hipérbola.
Estudiemos ahora la posición de dos puntos sobre la cónica que merecen alguna atención. El primero es el punto que se encuentra justo encima del foco, es decir $x=F$. La distancia vertical del eje de simetría a este punto se conoce como el semilatus rectum y se denota como $p$. Reemplazando en la Ec. (ecuacion_directriz):
$$ p^2=(e^2-1)F^2+2F^2-F^2 $$de donde se obtiene:
$$ p=eF $$El otro punto es el apside más cercano a la directriz. Si llamamos $\alpha$ a la distancia de ese punto a la directriz y usamos la definición de la cónica en la Ec. (conica_razon_cartesianas) obtenemos:
\begin{equation} \label{eq:alpha} \alpha=\frac{F}{1+e} \end{equation}Por otro lado la distancia del foco al apside más cercano, que llamaremos periapsis $q$, viene dada en términos de $F$, $e$ por:
$$ \begin{array}{rcl} q & = & F-\alpha \\ & = & eF/(1+e) \\ \end{array} $$o bien,
\begin{equation} \label{eq:q} q=\frac{p}{1+e} \end{equation}Si trasladamos ahora la Ec. (ecuacion_directriz) el origen de coordenadas en el punto O, es decir si reemplazamos $x_d=x_a+\alpha$, $y_d=y_a$ obtenemos:
\begin{equation} \label{eq:ecuacion_directriz_trasladada} y_a^2 = 2 e F x_a + (e^2-1) x_a^2 \end{equation}que comparando con la Ec. (ecuacion_apside) nos permite escribir los parámetros de tamaño $L$ y forma $\eta$ en la definición de Apolonio, en función de la excentricidad $e$ y semilatus rectum $p$:
$$ L = 2p\\ $$\begin{equation} \label{eq:eta_apolonio} \eta = e^2-1 \end{equation}De esta última relación y de la frase final de la Sección Del nombre al algebra en la que identificamos a la circunferencia como la cónica con $\eta=-1$, concluimos nuevamente que la circunferencia no es más que una elipse para la cuál $e=0$.
4.2.4. Síntesis geométrica¶
En resumen podemos decir que las curvas cónicas, o al menos sus principios de construcción, eran conocidas en Grecia posiblemente desde el tiempo de los pitagóricos. Sin embargo, fue Apolonio de Perga quién profundizo en las propiedades geométricas y "algebraicas" de estas curvas. Su aplicación astronómica, sin embargo, era desconocida y fue descubierta solo hasta los trabajos de Kepler en los 1600.
En términos geométricos simples las cónicas con el resultado de la intersección de un cono con un plano con cuatro posibles inclinaciones respecto a su eje de simetría. A pesar de que esto implicaría que existen cuatro posibles cónicas, las definiciones posteriores demuestran que en realidad la circunferencia es un caso particular de la elipse ($\eta=-1$ o $e=0$.)
Toda cónica tiene: un eje de simetría, una recta directriz, un foco, un ápside (el periapsis o punto más cercano al foco) y un latus rectum (segmento perpendicular al eje y que pasa por el foco.) Las elipses tienen un segundo eje de simetría, perpendicular al primero y a distancias iguales de dos apsides y por la misma razón un segundo foco y un segundo latus rectum.
Las dimensiones y forma de una cónica se pueden describir, en general, en términos de dos parámetros:
Parametrización de Apolonio. Los parámetros son la longitud del latus rectum $L>0$ y el parámetro de Apolonio $-\infty<\eta<\infty$. De acuerdo con $\eta$ las cónicas se clasifican en: parábola ($\eta=0$), circunferencia o elipse ($\eta<0$) e hipérbola ($\eta>0$).
Parametrización de Arquímedes. Los parámetros son el semilatus rectum $p>0$ y la excéntricidad $0\leq e<1$. De acuerdo con $e$ las cónicas se clasifican en: parábola ($e=1$), circunferencia y elipse ($0\leq e<1$) e hipérbola ($e>1$).
Se acostumbra usar más la parametrización de Arquímedes y es la que utilizaremos en lo sucesivo en el libro.
Si se construye un sistema de coordenadas en el plano de la cónica, con eje $x$ en la dirección del eje de simetría, dependiendo de la localización del origen, las coordenadas cartesianas de los puntos sobre la cónica obedecen las ecuaciones:
- Origen en el ápside: $y_a^2 = 2p x_a + (e^2-1) x_a^2$.
- Origen en la directriz: $y_d^2 = (e^2-1) x_d^2 + (2p/e) x_d - (p/e)^2$
Esta última ecuación no es conveniente para describir la circunferencia.
Indice | Previo: Fundamentos.Calculo.Series | Siguiente: Fundamentos.Conicas.Algebra