Indice | Previo: Fundamentos.Conicas.Geometria | Siguiente: Fundamentos.Conicas.Anomalias

4.2.5. Descripción algebraica

Si bien en las secciones anteriores adscribimos a Apolonio y a Arquímedes (y a sus contemporáneos griegos) la descripción de las cónicas en términos de ecuaciones algebraicas con sus coordenadas como variables, en realidad esta descripción solo apareció en la historia con el surgimiento de la moderna Geometría analítica en los 1600 y de la mano de René Descartes ("René decart") y Pierre de Fermat ("pier de fermat").

Ahora bien, la forma algebraica general que vimos en la Ec. (ecuacion_apside)

\begin{equation} \label{eq:ecuacion_apside_pe} y_a^2-2p x_a -(e^2-1) x_a^2 = 0 \end{equation}

no es precisamente ni la fórmula más simple, ni la más general.

En esta sección exploraremos a fondo las propiedades algebraicas de las cónicas y al hacerlo descubriremos algunas propiedades importantes que usaremos en la mecánica celeste.

Si queremos escribir la ecuación de la cónica en otras formas, podemos, como lo hicimos en el caso de la Eq. ecuacion_directriz_trasladada, aplicar dos tipos de transformaciones al sistema de coordenadas:

  • Una traslación, que implica simplemente modificar la posición del origen de coordenadas, tal y como hicimos en la Sección Directriz de las cónicas al pasar del origen en la directriz a un origen en el ápisde.

  • Una rotación, que implica modificar la dirección de los ejes coordenados. Esta es una transformación más compleja pero que resultará particularmente útil en la aplicación de las cónicas en mecánica celeste.

4.2.6. Ecuación respecto al centro

Para encontrar una forma más simple de la ecuación de la cónica, podemos realizar una traslación del origen, del apside (respecto al cuál esta escrita la Ec. ecuacion_apside) a un punto C en el cuál la forma algebraica, por ejemplo solo contenga términos cuadráticos en las coordenadas.

Una traslación a lo largo del eje $x$ se escribe como:

\begin{eqnarray} \label{eq:traslacion_centro} x_a & = & x_c + a \\ \nonumber y_a & = & y_c \end{eqnarray}

donde $a$ es la distancia del origen de las nuevas coordenadas $x_c,y_c$ (punto C), al origen de las coordenadas $x_a,y_a$ (apside).

Reemplazando las Ecs. (traslacion_centro) en la ecuación de la cónica obtenemos:

$$ y_a^2-2p(x_c+a)+(1-e^2)(x_c+a)^2=0 $$

que después de una manipulación algebraica se puede escribir en la forma:

$$ y_c^2+(1-e^2)x_c^2+2[(1-e^2)a-p]x_c=2pa-(1-e^2)a^2 $$

Como el valor de $a$ es libre, podemos escogerlo de modo el término lineal en $x_c$ desaparezca. Con esta elección el valor de esta constante queda:

\begin{equation} \label{eq:semiejemayor} a=\frac{p}{1-e^2} \end{equation}

Descubrimos aquí que el desplazamiento al punto $C$ solo tiene el efecto deseado en el caso en el que $e\neq 1$ (elipse e hipérbola). Para el caso de la parábola, en realidad la forma más simple de la ecuación sigue siendo aquella referida al apside (Ec. ecuacion_apside), $y_d^2=2px_d$.

La ecuación de la elipse o de la hipérbola se puede escribir entonces como:

$$ \frac{x_c^2}{p^2/(1-e^2)^2}+\frac{y_c^2}{p^2/(1-e^2)}=1 $$

o en términos del parámetro $a$:

\begin{equation} \label{eq:ecuacion_centro} \frac{x_c^2}{a^2}+\frac{y_c^2}{b^2}=1 \end{equation}

en el que se ha definido:

\begin{equation} \label{eq:semiejemenor} b^2\equiv a^2(1-e^2) \end{equation}

4.2.7. Eje mayor y menor de la elipse

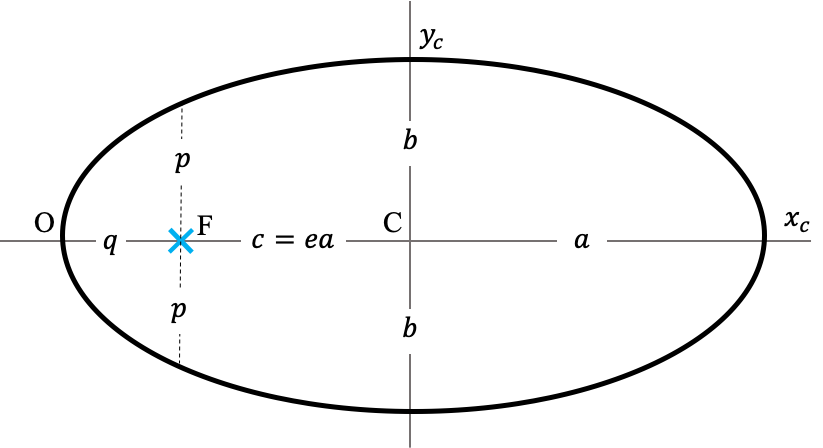
La ecuación (ecuacion_centro) es la forma más simple y simétrica de una elipse o una hipérbola. Pero ¿qué interpretación geométrica tienen los parámetros $a$, $b$ y el punto C.

En el caso de la elipse, podemos ver que cuando $y_c=0$ (apsides), $x_c=\pm a$ (ver Figura (elipse)), es decir $a$ es la distancia de los apsides al punto C, alrededor del cuál la elipse es simétrica. Llamamos a la constante $a$ en este caso el semieje mayor de la elipse y C es el centro geométrico de la figura.

También en el caso de la elipse, haciendo $x_c=0$ resulta $y_c=\pm b$, de donde interpretamos a $b=a\sqrt{1-e^2}$ como la distancia a los extremos del eje menor al centro de la elipse. Por esta misma razón llamamos a la constante $b$ el semieje menor.

Parámetros geométricos de la elipse referidos al apside O, el foco F y el centro C: $a$ semieje mayor, $b$ semieje menor, $p$ *semilatus rectum*, $e$ excentricidad, $c$ distancia foco-centro.

Figura 4.20. Parámetros geométricos de la elipse referidos al apside O, el foco F y el centro C: $a$ semieje mayor, $b$ semieje menor, $p$ *semilatus rectum*, $e$ excentricidad, $c$ distancia foco-centro.

Un resultado interesante, que podemos agregar a las definiciones geométricas de Apolonio y Democrito, resulta al combinar la definición de $a$ con la distancia de un apside al foco más cercano $q$. Es claro de la Figura (elipse_hiperbola) que la distancia entre el centro y el foco de la elipse, que llamaremos en lo sucesivo $c$ es:

\begin{eqnarray} \nonumber c & = & a-q\\ \nonumber & = & \frac{p}{1-e^2}-\frac{p}{1+e}\\ \nonumber \end{eqnarray}

o en términos simples:

\begin{equation} c = ae \end{equation}

Este resultado se puede interpretar diciendo que la excentricidad de una elipse $e=c/a$ es el grado en el que el foco esta desplazado a partir del centro geométrico de la figura y medido en unidades del semieje mayor $a$. De allí precisamente el nombre de este parámetro.

Uno podría entonces cuantificar la excentricidad de una elipse como un porcentaje. Así por ejemplo, la órbita osculatriz de Marte (volveremos sobre este concepto en el Capítulo El problema de los dos cuerpos), que fue el planeta utilizado por Kepler para descubrir que las órbitas planetarias eran elipses, es una elipse con una excentricidad de $9.3\%$.

Es decir, el centro geométrico de la órbita de Marte esta desplazado respecto a su foco (donde se ubica el Sol o más precisamente el centro de masa del Sistema Solar) un $9.3\%$ del eje mayor (la distancia promedio de Marte al Sol.) Este desplazamiento (que es significativo) fue la clave precisamente de porque fue más fácil para Kepler deducir la elipticidad de la trayectoria de ese planeta, de lo que lo fue para todos los astrónomos antes que él deducirlo usando la trayectoria de todos los demás planetas (en comparación las excentricidades de las órbitas osculatrices de la Tierra y de Júpiter, por ejemplo, son $1.6\%$ y $4.8\%, respectivamente.)

Utilice el código interactivo que viene con las libretas en la versión electrónica del libro para visualizar la forma de las órbitas de los planetas mencionados y ver realmente, que tan diferentes de una circunferencia son.

Figura 4.21.

4.2.8. Parámetros de la hipérbola

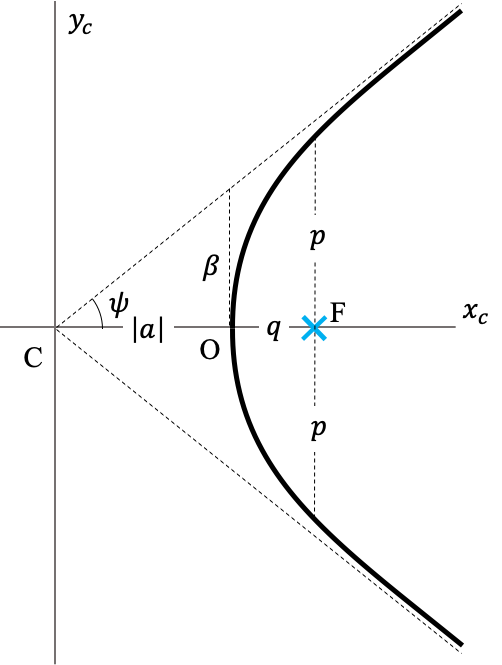
La interpretación geométrica de $a$ y $b$ en el caso de la hipérbola ($e>1$) es un poco más complicada (ver la Figura (hiperbola)).

Para empezar el valor del parámetro $a=p/(1-e^2)$ es negativo. Esto implica que el punto $C$, que hace la ecuación de la hipérbola la más sencilla posible, esta a la izquierda del apside, contrario a lo que pasa con la elipse. Llamamos a C, no el centro de la hipérbola sino su vértice.

No debemos confundir sin embargo el eje $y_c$ en la Figura (hiperbola) con la directriz de la hipérbola (ver Figura (conicas_directriz)) que en realidad esta situada a una distancia $\alpha=a(1-e)/e$ (ver Ec. alpha.) La directriz y el eje $y_c$ se aproximan una a otra cuando $e\rightarrow \infty$.

Parámetros geométricos de la hipérbola referidos al apside O, el foco F y el vértice C: $a$ distancia al vértice (llamado con frecuencia también semieje mayor aunque en la hipérbola no hay tal), $

Figura 4.22. Parámetros geométricos de la hipérbola referidos al apside O, el foco F y el vértice C: $a$ distancia al vértice (llamado con frecuencia también semieje mayor aunque en la hipérbola no hay tal), $

El parámetro $b^2=a^2(1-e^2)$ es inconveniente dado que en este caso $e>1$ y por lo tanto $b$ debería ser un número imaginario. Para evitar este inconveniente reescribimos la ecuación de la hipérbola Ec. (ecuacion_centro) como:

\begin{equation} \label{eq:ecuacion_centro_hiperbola} \frac{x_c^2}{a^2}-\frac{y_c^2}{\beta^2}=1 \end{equation}

y definimos:

\begin{equation} \label{eq:beta} \beta\equiv |a|\sqrt{e^2-1} \end{equation}

¿Cuál es la interpretación geométrica de $\beta$? Si despejamos $y_c$ de la Ec. (ecuacion_centro_hiperbola) tenemos:

$$ y_c=\pm\beta\sqrt{\frac{x_c^2}{a^2}-1} $$

donde los signos $\pm$ corresponden a las "ramas" superior e inferior de la hipérbola.

Aquí descubrimos una interesante propiedad de esta cónica: cuando $x_c\rightarrow \infty$, la hipérbola se aproxima a las recta:

$$ y_c\rightarrow\pm\frac{\beta}{|a|} x_c $$

que llamamos asíntotas. La pendiente de las asíntotas, $\beta/|a|$ nos permite identificar a $\beta$ como una cantidad que cuántifica el grado de apertura de la hipérbola respecto a su eje de simetría: a mayor $\beta$ (mayor excentricidad), mayor es la pendiente de las asíntotas y más cerca esta la hipérbola de una línea recta paralela a la directriz.

Otra manera de cuantificar la pendiente de las asintotas es usar el ángulo $\psi$:

$$ \tan\psi \equiv \frac{\beta}{|a|} $$

No es difícil mostrar (ver problemas al final del capítulo), a partir de la definición anterior, que:

\begin{equation} \label{eq:cos_psi} \cos\psi = \frac{1}{e} \end{equation}

Para poner en un contexto astronómico este resultado, podemos mencionar que en 2019 fue descubierto un cometa proveniente del espacio interestelar, hoy conocido como el 2I/Borisov, cuya trayectoria respecto al centro de masa del sistema solar es una hipérbola con $e=3.35$. Usando la Ec. (cos_psi) podemos calcular que las asíntotas de su órbita se abren en un ángulo extremo de

In [1]:
#Cometa interestelar 2I/Borisov
e=3.35

from numpy import arccos
psi=arccos(1/e)

Psi = 72.63202008811639 grados

Utilice el código interactivo que viene con las libretas en la versión electrónica del libro para visualizar la forma de la órbita del 2I/Borisov.

Figura 4.23.

4.2.9. Rotación de las cónicas en el plano

Al comenzar la Sección Descripción algebraica de las cónicas, habíamos mencionado dos posibles transformaciones que nos conducían a la forma algebraica más simple (la que obtuvimos en la Sección Ecuación respecto al centro) y a la más general. La primera la obtuvimos simplemente aplicando una traslación de los ejes coordenados:

$$ \begin{array}{rcl} x_c &=& x_a-c\\ y_c &=& y_a \end{array} $$

Para obtener la forma más general, nos proponemos ahora realizar una rotación.

Si llamamos $x'$, $y'$, $z'$ a las coordenadas de un punto con respecto a los ejes rotados, puede demostrarse (ver problemas al final del capítulo) que estas se relacionan con las coordenadas del mismo punto en el sistema alineado con la cónica (eje $x$ en dirección del eje de simetría) a través de:

\begin{equation} \label{eq:rotacion2d} \begin{array}{rcl} x' & = & x \cos\theta + y \sin\theta \\ y' & = & - x \sin\theta + y \cos\theta \\ z' & = & z \\ \end{array} \end{equation}

donde $\theta$ es el ángulo que forma el eje $x'$ con el eje $x$ (ver Figura (rotacion).)

Matricialmente estas relaciones se pueden escribir como:

\begin{equation} \label{eq:rotacion2d_matricial} \left( \begin{array}{c} x' \\ y' \\ z' \end{array} \right) = R_z(\theta) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) \end{equation}

donde la matriz $R_z(\theta)$ esta dada por:

\begin{equation} \label{eq:matriz_rotacion2d} R_z(\theta) = \left( \begin{array}{ccc} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \end{equation}

y el subíndice $z$ indica que la rotación se realiza alrededor de este eje.

La matriz de rotación $R_z(\theta)$ es una matriz unitaria que tiene las siguientes propiedades:

  • Determinante, $\det R_z=1$.
  • Inversa, $R_z^{-1}=R_z^T$

Esta última propiedad implica que:

\begin{equation} \label{eq:inversa_matriz_rotacion} R_z^{-1}(\theta)=R_z(-\theta) \end{equation}

que será muy conveniente para lo que viene.

Usando las propiedades de $R_z$ podemos encontrar la transformación inversa a la Ec. (rotacion2d):

\begin{equation} \label{eq:rotacion2d_inversa_matricial} \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = R_z(-\theta) \left( \begin{array}{c} x' \\ y' \\ z' \end{array} \right) \end{equation}

o explícitamente:

\begin{equation} \label{eq:rotacion2d_inversa} \begin{array}{rcl} x & = & x' \cos\theta - y' \sin\theta \\ x & = & x' \sin\theta + y' \cos\theta \\ z & = & z' \\ \end{array} \end{equation}

El sistema SPICE contiene una rutina útil para definir de manera sencilla una matriz de rotación dado un ángulo y un eje respecto al que se realiza la rotación:

In [3]:
from spiceypy import rotate
from numpy import pi
Rz=rotate(pi/6,3)

Rz(30 grados) = 
[[ 0.8660254  0.5        0.       ]
 [-0.5        0.8660254  0.       ]
 [ 0.         0.         1.       ]]

Que coincide con la definición dada por la Ec. (matriz_rotacion2d).

4.2.1. Ecuación general de las cónicas

Qué pasa entonces si, partiendo de la ecuación general respecto al apside (Ec. ecuacion_apside_pe) hacemos primero una traslación a un punto con coordenadas $(t_x,t_y)$:

$$ (y+t_y)^2-2p(x+t_x)-(e^2-1)(x+t_x)^2=0 $$

y una vez trasladados al nuevo origen, realizamos una rotación a unos nuevos ejes $(x',y')$ realizando para ello la transformación dada por las Ecs. (rotacion2d_inversa):

$$ [(x'\sin\theta + y'\cos\theta)+t_y]^2-2p [(x'\cos\theta - y'\sin\theta)+t_x] -(e^2-1) [(x'\cos\theta - y'\sin\theta)+t_x]^2 = 0 $$

Expandiendo y recogiendo términos comunes, la ecuación general de una cónica trasladada y rotada será:

\begin{equation} \label{eq:ecuacion_conica_trasladada_rotada} \begin{array}{rcc} x'^2 (1- e^2 \cos^2\theta)+x'y'(e^2 \sin2\theta)+y'^2 (1- e^2 \sin^2\theta) & + & \\ x' [2 t_y \sin\theta - 2 p \cos\theta + 2 t_x \cos\theta (1-e^2)] & + & \\ y' [2 t_y \cos\theta + 2 p \sin\theta - 2 t_x \sin\theta (1-e^2)] & + & \\ t_x^2 (1- e^2) - 2 p t_x + t_y^2 & = & 0 \end{array} \end{equation}

que puede escribirse de forma general, como:

\begin{equation} \label{eq:ecuacion_general} \displaystyle Ax'^2 + Bx'y' + Cy'^2 + Dx' + Ey' + F = 0 \end{equation}

con:

\begin{equation} \label{eq:ecuacion_general_coeficientes} \begin{array}{rcl} A &=& 1 - e^2 \cos^2\theta\\ B &=& e^2 \sin2\theta\\ C &=& 1 - e^2 \sin^2\theta\\ D &=& 2 t_y \sin\theta - 2 p \cos\theta + 2 t_x \cos\theta (1-e^2)\\ E &=& 2 t_y \cos\theta + 2 p \sin\theta - 2 t_x \sin\theta (1-e^2)\\ F &=& t_x^2 (1- e^2) - 2 p t_x + t_y^2 \end{array} \end{equation}

Es decir, cualquier curva en el plano cuyos puntos obedezcan una ecuación cuadrática general de la forma Ec. (ecuacion_general) es una cónica con una orientación, tamaño, forma y posición de los apsides que dependerá de los coeficientes $A$, $B$, $C$, $D$, $E$ y $F$.

Dada la ecuación algebraica de una cónica, expresada en la forma cuadrática general (Ec. ecuacion_general), es posible, usando los coeficiende $A$, $B$ y $C$ determinar qué tipo de cónica y su orientación en el esepacio.

Para ello es posible, combinando algunas de las Ecs. (\ref{:ecuacion_general_coeficientes}), demostrar que:

\begin{equation} \label{eq:eta_ecuacion_general} \eta=1-(A+C) \end{equation}

y por otro lado:

\begin{equation} \label{eq:teta_ecuacion_general} \tan 2\theta=\frac{B}{C-A} \end{equation}

Si además se usan los valores de los coeficientes $D$ y $E$, es posible determinar la ordenada del vértice de la cónica:

\begin{equation} \label{eq:ty_ecuacion_general} t_y=\frac{D\sin\theta+E\cos\theta}{2} \end{equation}

Expresiones mucho más complejas pueden derivarse para $t_x$ y para $p$ en función de los coeficientes $D$, $E$ y $F$, que también dependen de ellos (ver problemas al final del capítulo.) Sin embargo, una vez el apside de la cónica ha sido localizada sobre el eje de las abcisas (realizando la traslación inversa $-t_y$) y ha sido rotada en un ángulo $\theta$ dado por la Ec. (teta_ecuacion_general) para que su eje de simetría coincida con el eje $x$, las demás propiedades de la curva pueden obtenerse más fácilmente.

4.2.11. Gráfico de una cónica rotada en el plano

Podemos poner en práctica algunos de los resultados de las secciones anteriores (siempre es importante hacerlo para garantizar que todo se ha entendido bien), construyendo numéricamente una cónica con la Ec. (ecuacion_apside_pe) y aplicando traslaciones y rotaciones a la misma para ver el efecto y escribir la ecuación general cuadrática (Ec. ecuacion_general) que la describe.

Comencemos, escogiendo las propiedades de nuestra cónica y determinando, el rango de valores de las coordenadas $x_a$ de los puntos sobre la cónica, en el sistema de coordenadas que tiene origen en el ápside:

In [5]:
p=10.0
e=0.8

#Parametro eta
eta=e**2-1

#Conjunto de valores de x de la cónica
from numpy import linspace
if e==1:
    a=p
else:
    a=p/(1-e**2)

#Rango de valores de x
xs=linspace(0,2*abs(a),100)

Nótese que $a$ no esta definido en el caso de una parábola $e=1$ (para una elipse y una hipérbola $a=p/(1-e^2)$, ver Ec. semiejemayor.) Por esa razón en el algoritmo anterior hemos escogido definir $a\equiv p$ cuando $e=1$, únicamente con el propósito de usar una sola expresión xs=linspace(0,2*abs(a),100) para calcular el rango de valores de las abcisas de la cónica.

Si bien sabemos que en el caso de parábolas e hipérbolas, los valores de las abcisas son $x_a\in [0,\infty)$ (ver Figura (conicas_apolonio)), para una elipse es claro que $x_a\in [0,2a]$ (ver Figura (elipse).)

Con los valores de $x$ podemos ahora usar la Ec. (ecuacion_apside_pe) para calcular los valores de la ordenada, tanto para la rama superior de la cónica (por encima del eje de simetría) como para la inferior:

In [6]:
#Ecuación de la cónica
from numpy import sqrt
ys_sup=sqrt(2*p*xs+eta*xs**2)
ys_inf=-sqrt(2*p*xs+eta*xs**2)

Para los propósito de graficar la cónica, debemos duplicar los valores de la lista xs. Sin embargo, y por razones que veremos abajo, lo haremos ordenando de forma especial las coordenadas de los puntos, comenzando primero con el punto más lejano al origen ($x=2a$ o xs[-1],ys[-1]), llegando hasta el origen mismo xs[0],ys[0] y de allí regresando de nuevo al punto más lejano.

En Python esta "compleja" operación puede abreviarse usando la sintaxis genera para extraer tajadas de los arreglos:

In [7]:
from numpy import append,zeros_like
xs=append(xs[::-1],xs)
ys=append(ys_sup[::-1],ys_inf)
zs=zeros_like(xs)

Un gráfico de los puntos de la cónica en el sistema de referencia del ápside srá:

In [8]:
import matplotlib.pyplot as plt
fig=plt.figure()
ax=fig.gca()

ax.plot(xs,ys,'b-')

from pymcel.plot import fija_ejes_proporcionales
valores=(xs,ys)
fija_ejes_proporcionales(ax,valores,xmin=0,ycm=0);
ax.grid()

Figura 4.24.

Ahora podemos trasladar la cónica:

In [9]:
#Parámetros de la traslación
tx=15.0
ty=-10.0

#Coordenadas trasladadas
xs=xs-tx
ys=ys-ty

Construimos la matriz de rotación usando las rutinas de SPICE (ver Alg. spice_rotate):

In [10]:
from spiceypy import rotate
from numpy import pi
teta=pi/6
Rz=rotate(teta,3)

La rotación de los puntos de la cónica contenidos en las listas xs, ys usando la Ec. (rotacion2d_matricial), no es tan trivial en Python. Para ello definiremos una rutina general que usaremos más adelante en el libro:

In [11]:
def rota_puntos(R,x,y,z):
    from spiceypy import mxv
    from numpy import zeros_like
    N=len(x)
    xp=zeros_like(x)
    yp=zeros_like(y)
    zp=zeros_like(z)
    for i in range(N):
        xp[i],yp[i],zp[i]=mxv(R,[x[i],y[i],z[i]])
    return xp,yp,zp

Los puntos rotados de la cónica serán:

In [12]:
xps,yps,zps=rota_puntos(Rz,xs,ys,zs)

Y una gráfica de los puntos rotados:

In [13]:
import matplotlib.pyplot as plt
fig=plt.figure()
ax=fig.gca()

ax.plot(xps,yps,'b-')

from pymcel.plot import fija_ejes_proporcionales
valores=(xps,yps)
fija_ejes_proporcionales(ax,valores);
ax.grid()

Figura 4.25.

Los valores de los coeficientes del polinomio de segundo grado $P(x,y)=Ax^2+By^2+Cxy+Dx+Ey+F$ que describe los puntos del gráfico anterior, son (Ec. ecuacion_general_coeficientes):

In [14]:
from numpy import sin,cos
A=1-e**2*cos(teta)**2
B=e**2*sin(2*teta)
C=1-e**2*sin(teta)**2
D=2*ty*sin(teta)-2*p*cos(teta)+2*tx*cos(teta)*(1-e**2)
E=2*ty*cos(teta)+2*p*sin(teta)-2*tx*sin(teta)*(1-e**2)
F=tx**2*(1-e**2)-2*p*tx+ty**2

A = 0.5199999999999998
B = 0.5542562584220408
C = 0.84
D = -17.967433714816835
E = -12.720508075688773
F = -119.00000000000003
Ecuación: (0.52)x^2+(0.55)xy+(0.84)y^2+(-18)x+(-13)y+(-119.0)=0

Podemos ahora verificar la afirmación que los puntos de la cónica satisfacen la ecuación $P(x,y)=0$ (Ec. ecuacion_general), construyendo primero una rutina para calcular, dado cualquier punto $(x,y)$ el valor del polinomio $P(x,y)$:

In [16]:
def polinomio_segundo_grado(coeficientes,x,y):
    A,B,C,D,E,F=coeficientes
    P=A*x**2+B*x*y+C*y**2+D*x+E*y+F
    return P

Si calculamos el valor de $P(x,y)$ para todos los puntos xps y yps verificamos la afirmación:

In [17]:
coeficientes=A,B,C,D,E,F
Pxpsyps=polinomio_segundo_grado(coeficientes,xps,yps)
In [18]:
print(f"P(xps,yps):\n{Pxpsyps[:5]}...")

P(xps,yps):
[ 2.84217094e-14 -1.13686838e-13 -1.13686838e-13 -7.10542736e-14
 -5.68434189e-14]...

O para verificarlo en todos los puntos, podemos sumar el valor absoluto de los valores de Pxpsyps:

In [19]:
Psum=sum(abs(Pxpsyps))

Sum |P(xps,yps)| = 1.1738165994756855e-11

Finalmente podemos poner a prueba las Ecs. (eq:eta_ecuacion_general), (teta_ecuacion_general) y (ty_ecuacion_general):

In [21]:
#Parámetro de forma
eta_num=1-(A+C)

#Ángulo
from numpy import arctan,sin,cos
teta_num=0.5*arctan(B/(C-A))

#Desplazamiento vertical
ty_num=(D*sin(teta_num)+E*cos(teta_num))/2

eta original = -0.36, eta numérico = -0.36
teta original = 30, teta numérico = 30
ty original = -10, ty numérico = -10

Como era de esperarse, la coincidencia es perfecta.

4.2.12. Síntesis algebraica

En la Sección Del nombre al álgebra mostramos como las definiciones abstractas de la antigüedad, basadas en áreas y proporciones, se convirtieron en la edad baja edad media y el renacimiento, en ecuaciones algebraicas. Las representaciones algebraicas permiten describir de forma sintética y poderosa el lugar geométrico de las cónicas.

En las secciones precedentes hemos visto como la descripción algebraica de las cónicas depende de donde coloquemos el origen o en que dirección escojamos los ejes del sistema de coordenadas. De acuerdo a estas elecciones reconocimos hasta ahora 4 formas distintas de describir algebraicamente cualquier cónica, una vez especificados un parámetro de tamaño, por ejemplo el semilatus rectum $p$ y uno de forma, por ejemplo la excentricidad $e$:

  • Ecuación respecto al apside (origen en el ápside, eje $x$ sobre el eje de simetría, Ec. ecuacion_apside): $$ y_a^2-2p x_a -(e^2-1) x_a^2 = 0 $$

  • Ecuación respecto a la directriz (origen en la directriz, eje $x$ sobre el eje de simetría, Ec. directriz):

    $$ y_d^2 - 2pe x_d -(e^2-1) x_d^2 + e^2p^2=0 $$

  • Ecuación respecto al centro (origen en el centro de simetría, eje $x$ sobre el eje de simetría, Ec. ecuacion_centro, solo valida para $e\neq 1$):

    $$ \frac{x_c^2}{a^2}\pm\frac{y_c^2}{b^2}=1 $$

    donde $a^2=p/(1-e^2)$, el signo "$+$" es para elipses ($e<1$) en cuyo caso $b^2=a^2(1-e^2)$ y el signo "$-$" es para hipérbola ($e>1$) para el cuál $b^2=\beta^2=a^2(e^2-1)$.

  • Ecuación general (origen en $t_x,t_y$ y eje $x'$ rotado un ángulo $\theta$ respecto al eje de simetría, Ec. ecuacion_general):

    $$ Ax'^2 + Bx'y' + Cy'^2 + Dx' + Ey' + F = 0 $$ con:

    $$ \begin{array}{rcl} A &=& 1 - e^2 \cos^2\theta\\ B &=& e^2 \sin2\theta\\ C &=& 1 - e^2 \sin^2\theta\\ D &=& 2 t_y \sin\theta - 2 p \cos\theta + 2 t_x \cos\theta (1-e^2)\\ E &=& 2 t_y \cos\theta + 2 p \sin\theta - 2 t_x \sin\theta (1-e^2)\\ F &=& t_x^2 (1- e^2) - 2 p t_x + t_y^2. \end{array} $$

Indice | Previo: Fundamentos.Conicas.Geometria | Siguiente: Fundamentos.Conicas.Anomalias