Indice | Previo: Mecanica.Dinamica.Cantidades | Siguiente: Mecanica.Dinamica.SistemaParticulas
Un pooco de historia: Los Principia de Newton. En abril de 1687 y después de trabajar tan solo durante 18 meses, Newton completo las 550 páginas del manuscrito que se convertiría en la primera edición de sus Philosophiæ Naturalis Principia Mathematica (Principios Matemáticos de la Filosofía Natural, ver Figura (principia))$^1$. A pesar del breve lapso de tiempo en el que escribió el libro, la obra recogía ideas acumuladas durante toda su carrera como filóso natural.
Los Principia (como se los llama de forma abreviada) es una obra revolucionaria e influyente que buscaba en últimas presentar y desarrollar las implicaciones una teoría general para explicar el movimiento de los cuerpos bajo la influencia de la omnipresente fuerza de gravedad (postulada en la obra.) Fue motivada y tenía como fin último el de resolver el problema de más de 2.000 años de explicar el movimiento de los planetas, sus lunas y los cometas partiendo de las causas que los producen. En una palabra los Principia son el primer libro de Mecánica Celeste en la historia.
Los Principia se dividen en tres libros. El Libro I trata sobre los fundamentos de la mecánica de partículas. En él, Newton introduce los conceptos relativamente novedosos de masa, cantidad de movimiento, fuerza centrípeta y el original postulado de acción y reacción. Muchas de las ideas en este libro, como el mismo Newton lo reconocerían, en realidad compilaban y sistematizaban de ideas que venían discutiéndose entre los filósofos naturales por más de un siglo. Así por ejemplo, la denominada ley de inercia, que Newton formula como su primera ley, en realidad había sido planteada primero por Galileo y después por Pierre Gassendi y René Descartes. Por su parte, el postulado de fuerza había sido sugerido primero por Galileo Galilei.
El libro II aborda el problema del movimiento de los cuerpos en los fluídos (aire, agua, etc.) Tenía el propósito original de refutar la teoría Cartesiana del movimiento, que proponía, por ejemplo, que los planetas se movían alrededor del Sol impulsados hacia adelantes por la fuerza de vórtices creados en una sustancia omnipresente, el éter. En este libro Newton, entre otras cosas demuestra que las fuerzas exprimentadas por los cuerpos en un fluído no podrían explicar las leyes del movimiento planetario formuladas por Kepler en 1609 (y sobre las que volveremos en el Capítulo El problema de los dos cuerpos.)
El libro III titulado "Sobre el Sistema del Mundo" y el más importante para nosotros aquí, desarrolla en detalle la teoría de la gravedad. En un sucesión de teoremas, aplicados primero a las lunas de Júpiter, a las lunas de Saturno, a la Luna y finalmente a los planetas, Newton introduce su ley de gravitación universal en la forma presentada aquí en el Pos. principia. A continuación demuestra a partir de esta ley la validez de las leyes empíricas de Kepler (movimiento en elipses, ley de áreas y ley armónica.) Más adelante desarrolla en algún detalle su teoría del movimiento lunar, incluyendo las perturbaciones producidas por el Sol y desarrolla la teoría de las mareas que hoy aceptamos como correcta, y explica y describe el fenómeno de precesión de los equinoccios, que si bien se había descubierto desde el tiempo de los griegos no había recibido ninguna explicación satisfactoria en casi 2.000 años. Finalmente, yendo más allá de la teoría del movimiento orbital de Kepler, y usando su ley de gravitación universal, Newton explica el movimiento de los cometas que se mueven, según él en órbitas aproximadamente parabólicas, resolviendo de una vez por todas la discusión sobre la naturaleza celeste de estos cuerpos.
5.3.4. Postulado de fuerzas¶
La manera original en la que Newton formuló sus postulados clásicos sobre la relación entre las fuerzas aplicadas y el movimiento resultante, ha cambiado mucho en los 350 años que nos separan de la publicación de los Principia. Hoy, existen maneras alternativas de formular estos principios y leyes (algunas de las cuáles serán desarrolladas en el libro) manteniendo los efectos prácticos de la teoría.
A continuación usaremos una presentación de la mecánica newtoniana muy propia del estilo de este libro y que sintetiza en un esquema formal, sobre la base de los conceptos y cantidades definidas en las secciones anteriores, sus postulados (leyes) y teoremas.
Nota: Una formulación original. El lector puede encontrar relativamente extraña nuestra formulación (muy diferente a la que encontrará en los textos de mecánica básica.) La razón de fondo estriba esencialmente en la manera como hemos definido antes el concepto de fuerza. Esta formulación sin embargo, como veremos a lo largo del libro, además de contener los resultados básicos de la teoría conocidos por todos, ofrece algunas ventajas para su formulación en teorías del movimiento más general como la teoría de la relatividad.
La ley física en el corazón de la mecánica newtoniana se conoce como el postulado de fuerza:
Postulado: Postulado de Fuerzas. Si en un sistema de referencia inercial, una partícula esta sometida a una fuerza neta aplicada $\vec F$ (suma vectorial de las fuerzas aplicadas correspondientes a cada interacción que sufre la partícula en ese instante) su momento lineal cambiará instantáneamente a razón de:
$$ \dot{p}=\vec F $$
En otros términos, la fuerza resultante es siempre igual la fuerza neta aplicada:
$$ \vec{\cal F}=\vec F $$
Aunque está última expresión parece obvia y universal, no lo es. Recordemos que la fuerza aplicada $\vec F$ es una propiedad de las interacciones y su valor se cálcula a partir de los modelos epecíficos que las describen. En contraposición, la fuerza resultante $\vec{\cal F}$ (la razón de cambio del momento lineal) es un efecto observado en el movimiento de la partícula. El postulado fuerzas básicamente plantea que en todas las interacciones a las que se somete una partícula, la causa (fuerza aplicada) y el efecto (fuerza resultante o razón de cambio del momento lineal) tienen el mismo valor.
Es importante resaltar la condición de que el sistema de referencia sea inerical para que el postulado de fuerzas sea válido. En otras palabras, en sistemas de referencia no inerciales, la fuerza resultante no es igual a la fuerza aplicada. Volveremos sobre este caso en la Sección Dinámica en sistemas de referencia rotantes.
Por la suposición que hemos hecho desde el principio de que la masa de las partículas es constante, el postulado de fuerzas nos permite calcular la función de aceleración de las partículas que usamos en la e.d.m. (ver Ec. edm). Si reconocemos que por definición para una partícula $\dot{\vec p}=m\vec a$, el postulado de fuerzas se puede escribir como:
$$ \vec a = \frac{\vec F}{m} $$La e.d.m. de una partícula en función de las fuerzas aplicadas queda:
\begin{equation} \label{eq:edm_fuerzas_aplicadas} \ddot{\vec{r}}=\frac{\vec F}{m}. \end{equation}Nota: Ecuación de movimiento con fuerzas resultantes. Una relación idéntica a la Ec. (edm_fuerzas_aplicadas) es válida en el caso de las fuerzas resultandes:
\begin{equation} \label{eq:edm_fuerzas_resultantes} \ddot{\vec{r}}=\frac{\vec{\cal F}}{m} \end{equation}
Esta ecuación sin embargo no es un postulado de la mecánica, sino una forma de la definición misma de fuerza aplicada $\vec{\cal F}$ que introdujimos en la Sección cantidades dinámicas básicas.
Aunque la identidad matemática de las Ecs. (edm_fuerzas_aplicadas) y (edm_fuerzas_resultantes) nos permite escribir la ecuación de movimiento sin distinguir que tipo fuerzas están involucradas, no debemos olvidar la diferencia conceptual entre una aceleración producto de las interacciones (fuerza aplicada, Ec. edm_fuerzas_aplicadas) y aquella que es simplemente una manifestación del cambio en el momento lineal (fuerza aplicada, Ec. edm_fuerzas_resultantes).
La igualdad matemática, en sistemas inerciales, postulada entre la fuerza neta aplicada sobre una partícula y la fuerza resultante, permite extrapolar la definición de trabajo que presentamos en la Sección cantidades dinámicas básicas y derivar un importante teorema de la mecánica newtoniana:
Proposición 11.7. Teorema del tabajo y la energía. Si una partícula que en un sistema de referencia inercial, se mueve sobre una trayectoria entre dos puntos $\vec r_1$ (donde tiene velocidad $\vec v_1$) y $\vec r_2$ (donde tiene velocidad $\vec v_2$), esta sometida a una fuerza neta aplicada $\vec F$ que cambia de acuerdo a una función conocida y continua sobre la trayectoria, entonces, el trabajo realizado por la fuerza aplicada es $W = \int \vec{F}\cdot \mathrm{d}\vec r$ y la siguiente igualdad es válida:
$$ W = \Delta K $$
Donde $K=mv^2/2$.
5.3.5. Fuerzas conservativas y no conservativas¶
Una clasificación adicional de las fuerzas (tanto resultantes como aplicadas) surge al estudiar su circulación $\oint \vec F \cdot d\vec r$ (ver la Sección Integrales.) En términos físicos, la circulación de una fuerza (resultante o aplicada) es el trabajo total realizado por ella a lo largo de una trayectoria cerrada.
De acuerdo con la circulación las fuerzas se clasifican en:
Fuerzas conservativas: Una fuerza es conservativa si y solo sí, su circulación es nula:
\begin{equation} \label{eq:circulacion_nula} \oint \vec F\cdot d\vec r=0 \end{equation}
Una manera más frecuente (y física) de expresar esta propiedad (ver problemas al final del capítulo) es diciendo que el trabajo realizado por una fuerza conservativa entre dos puntos del espacio, es independiente de la trayectoria que esta siga entre esos puntos.
Por el teorema del tabajo y la energía, la circulación nula implica que la energía cinética de una partícula sometida a una fuerza conservativa, es la misma antes y después de recorrer una trayectoria cerrada. Este es precisamente el origen del adjetivo conservativo.
- Fuerzas no conservativas o disipativas: Una fuerza es no conservativa si su circulación es distinta de cero. En este caso, en virtud del teorema del trabajo y la energía, la energía cinética de la partícula antes y después de realizar el recorrido cerrado, será diferente. Es por esta razón que a este tipo de fuerzas se las llama también fuerzas disipativas.
Nota: La fuerza como campo vectorial. Nótese que al definir la circulación o al hablar aquí del trabajo realizado sin importar el camino seguido por la partícula, estamos asumiendo que en todos los puntos del espacio a los que tiene acceso la partícula, podemos calcular el valor de la fuerza $\vec F$. En este sentido la fuerza ya no es simplemente un vector más, sino que se convierte en lo que en el cálculo se conoce como un campo vectorial, es decir, una función que asocia a cada punto del espacio un vector (ver la Sección Funciones.)
La propiedad expresada en la Ec. (circulacion_nula) implica, por el corolario al teorema de Stokes (Cor. circulacion_nula) que las fuerzas conservativas se pueden escribir como:
\begin{equation} \label{eq:funcion_energia_potencial} \vec F = -\vec{\nabla} U = -\partial_{\vec r} U \end{equation}donde el signo menos, que parece arbitrario, es una convención usada frecuentemente en física (y que se justificará en la siguiente sección.)
En mecánica llamamos a $U$ la función de energía potencial de la fuerza conservativa.
Las fuerzas conservativas pueden describirse o bien usando un campo escalar $U$ (el campo de energía portencial) o bien usando un campo vectorial $\vec F$ (como se acostumbra con todas las fuerzas, conservativas o no). El uso de una descripción o de la otra dependerá de la situación que estemos considerando.
5.3.6. Energía mecánica¶
Con la definición de la función de energía potencial, el trabajo realizado por una fuerza conservativa se puede escribir como:
\begin{eqnarray} \int \vec F\cdot \mathrm{d}\vec r & = & -\int \partial_{\vec r} U \cdot \mathrm{d}\vec r\nonumber\\ & = & -\int \mathrm{d}\mathrm{U}\nonumber\\ & = & -[U(\vec r_2)-U(\vec r_1)]\nonumber\\ & = & -\Delta U\nonumber \end{eqnarray}donde hemos usado, en su orden, la regla de la cadena (Teo. circulacion_nula) y la rela de Newton-Leibniz (Teo. circulacion_nula).
El teorema del trabajo y la energía (Teo. circulacion_nula) para una fuerza conservativa se escribe entonces como:
\begin{equation} \label{eq:deltaU_deltaK} \begin{array}{rcl} -\Delta U & = & \Delta K\\ \Delta(K+U) & = & 0. \end{array} \end{equation}Este último resultado implica que la cantidad $E\equiv K+U$ se conserva durante el movimiento de una partícula bajo la acción de una fuerza conservativa. Llamaremos a esta cantidad en lo sucesivo energía mecánica y a esta interesante propiedad (que es producto del teorema del trabajo y la energía), conservación de la energía mecánica.
El resultado anterior puede generalizarse cuando sobre la partícula actúan todo tipo de fuerzas, aplicadas o resultantes, conservativas o no conservativas:
Proposición: Conservación de la energía. Si una partícula se mueve en el espacio mientras esta sometida a fuerzas conservativas y no conservativas, el trabajo total realizado por las fuerzas no conservativas $W_{\rm NC}$ entre dos puntos cualquiera de la trayectoria es:
$$ W_\mathrm{NC} = \Delta E $$Donde $E\equiv K+\sum U_i$, siendo $\{U_i\}$ las funciones de energía potencial asociadas a todas las fuerza conservativas que actúan sobre la partícula. Llamamos a $E$ la energía mecánica total de la partícula.
5.3.7. ¿Ley de inercia?¶
En la historia de la mecánica, el concepto de inercia o movimiento inercial, y la ley de inercia de Newton, jugaron un papel fundamental en la ruptura con los conceptos dinámicos de la física Aristótelica que postulaban que todo movimiento necesitaba una causa motriz (una fuerza aplicada en nuestro caso.)
En los Principia y en sus reformulaciones posteriores (Chandrasekhar, 2003), la inercia aparece postulada como la primera ley movimiento.
En el esquema con el que hemos sintetizado la mecánica newtoniana aquí, la inercia no tiene que postularse, sino que en realidad es un teorema muy sencillo que se sigue (casi trivialmente) del postulado de fuerzas:
Proposición: Teorema de inercia. Si la fuerza resultante o la fuerza neta aplicada sobre una partícula es nula durante un cierto intervalo de tiempo $[t_1,t_2)$$^2$, su momento lineal en ese intervalo será constante e igual al momento lineal que tenía en $t_1$:
$$ \vec F(t\in[t_1,t_2))=\vec 0\Longleftrightarrow \vec p(t\in[t_1,t_2))=\vec{p}(t_1) $$
En otras palabras durante el intervalo considerado la partícula estará en reposo (si $\vec p(t_1)=\vec 0$) se moverá siguiendo una trayectoria rectilínea y con velocidad constante $\vec v=\vec p(t_1)/m$.
5.3.8. Postulado de acción y reacción¶
Postulado: Acción y reacción. En un sistema de referencia inercial en el que dos partículas 1 y 2 interactúan mutuamente, sea a través de fuerzas de contacto o de campo, se cumple que:
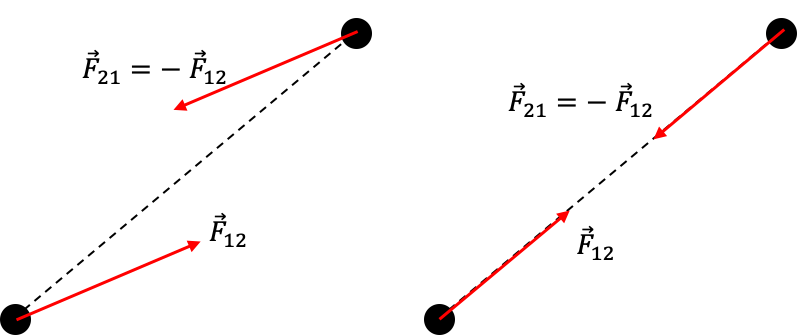
- (Forma débil del postulado de acción y reacción) la fuerza $\vec{F}_{12}$ que la partícula 1 experimenta por la interacción con la partícula 2 (que llamaremos acción), es igual pero de sentido contrario a la fuerza $\vec{F}_{21}$ que la partícula 2 experimenta por la interacción con la partícula 1 (que llamaremos reacción; ver panel izquierdo de la Figura (accion_reaccion).)
o bien,
- (Forma fuerte de la ley de acción y reacción) las fuerzas de acción y reacción, definidas arriba, son además paralelas a la línea que une las posiciones de las partículas (ver panel derecho de la Figura (accion_reaccion)).
Las consecuencias de este postulado son fundamentales en la mecánica y serán discutidas en la Sección Dinámica de sistemas de varias partículas.
5.3.9. Postulado de gravitación universal¶
Una de los más atrevidos y visionarios postulados de Newton sobre la naturaleza del movimiento de los cuerpos y en general del Universo, se conoce como la ley o postulado de gravitación universal que en su forma moderna propone:
Postulado de gravitación universal. Una partícula de masa $m_1$ situada en $\vec r_1$ ejerce sobre cualquier otra partícula de masa $m_2$ situada en un $\vec r_2$, una fuerza instantánea a distancia dada por:
$$ \vec F=-\frac{G m_1 m_2}{r^2}\hat r $$donde $\vec r\equiv\vec r_2-\vec r_1$ y $G=6.67408(31)\times 10^{-11}$ m$^3$ kg$^{-1}$ s$^{-2}$ $=(6.67408\pm 0.00031)\times 10^{-11}$ m$^3$ kg$^{-1}$ s$^{-2}$ es una constante de la naturaleza conocida como la constante de gravitación universal o constante de Cavendish.
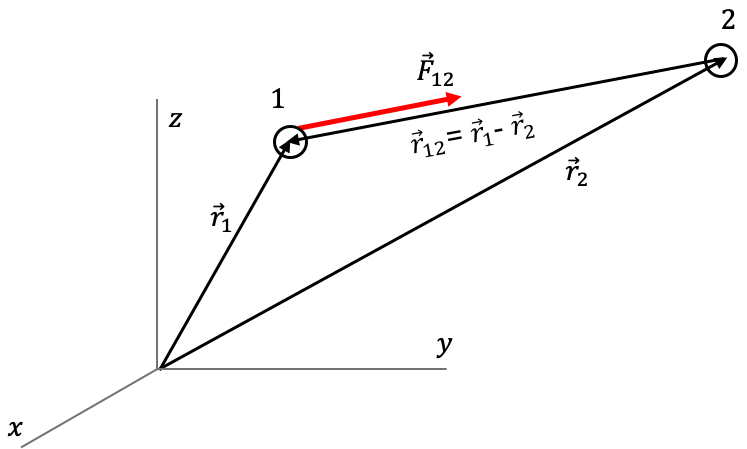
En lo sucesivo usaremos la notación más precisa y consistente (ver Figura (fuerza_gravitacional)):
\begin{equation} \label{eq:fuerza_gravitacional} \vec F_{12}=-\frac{G m_1 m_2}{r_{12}^3}\vec{r}_{12} \end{equation}Donde $\vec{r}_{12}\equiv\vec{r}_1-\vec{r}_2$.
Nótese que esta forma del postulado de gravitación universal, ofrece una expresión para la fuerza sobre la partícula 1 en lugar de la que ella ejerce sobre la partícula 2 (aunque por el postulado de acción y reacción son iguales). Además, el vector relativo $\vec{r}_{12}$ (ver Figura (fuerza_gravitacional)) va de la partícula 2 a la partícula 1 (en lugar de $\vec r$ que en el enunciado del postulado que va de la 1 a la 2). Asegúrese de entender claramente la definición y el sentido de estos vectores que serán usados con mucha frecuencia a lo largo del texto.
Nota: La fuerza de gravedad y la ley de acción y reacción. Como puede verse de la definición matemática de la fuerza de gravitación (Ec. fuerza_gravitacional), tanto ella como su reacción, satisfacen las condiciones del postulado fuerte de acción y reacción, lo que tendrá consecuencias fundamentales cuando estudiemos las simetrías y cantidades conservadas en sistemas de varias partículas interactuando gravitacionalmente.
5.3.1. La fuerza gravitacional de la Tierra, el Sol y la la Luna¶
Para poner en un contexto práctico las ideas de la sección anterior, calcularemos aquí la fuerza gravitacional ejercida por el Sol y la Tierra sobre la Luna.
Si bien el postulado de gravitación universal (Ec. fuerza_gravitacional), aplica solamente para partículas puntuales, como se explico desde el principio, dadas las dimensiones del Sistema Solar, podemos asumir que los tres cuerpos en cuestión son muy pequeños.
El cálculo de la Fuerza requiere que compilemos primero la información sobre las masas y distancias de estos cuerpos:
# Constante de gravitación
G=6.67408e-11 #m^3/kg s^2
#Masa de los cuerpos
M_tierra=5.97e24 #kg
M_luna=7.34e22 #kg
M_sol=1.98e30 #kg
#Distancia entre ellos
d_sol_tierra=149600000*1000 #m
d_tierra_luna=385000*1000 #m
d_sol_luna=d_sol_tierra-d_tierra_luna
Aunque la distancia entre el Sol y la Luna cambia continuamente debido al complejo movimiento de nuestro satélite, asumiremos, para nuestro sencillo cálculo, la mínima distancia entre ellos, es decir la distancia a la que se encuentran en la fase de Luna Nueva (cuando la Luna esta entre la Tierra y el Sol.)
Las fuerzas entre ellos serán por tanto:
F_sol_tierra=G*M_sol*M_tierra/d_sol_tierra**2
F_sol_luna=G*M_sol*M_luna/d_sol_luna**2
F_tierra_luna=G*M_tierra*M_luna/d_tierra_luna**2
Si bien, fuerzas tan grandes son difíciles de interpretar en términos cotidianos (la fuerza gravitacional que ejerce la Tierra sobre una persona con una masa de 60 kg es de apenas 590 N), un hecho "inesperado" llama la atención: la fuerza que ejerce el Sol sobre la Luna es más del doble que la que ejerce la Tierra sobre ella. ¿Será porque usamos la distancia de la Luna en la fase de nueva cuando está más cerca al Sol? ¿cuanto disminuirá la fuerza del Sol sobre la Luna si la ponemos en una posición cercana la fase de Luna Llena? ¿a qué distancia debería estar la Luna de la Tierra para que la fuerza de nuestro planeta sobre la primera igualará a la que siente del Sol? ¿órbita entonces la Luna al Sol o a la Tierra? y si ese es el caso ¿por qué la hemos considerado siempre nuestro "satélite"?
Dejamos al lector la discusión y solución de estas preguntas (algunas de las cuáles serán ampliadas en la sección de problemas al final del capítulo), pero no podemos dejar de mencionar que una importante motivación para los desarrollos de la mecánica celeste posteriores a los tiempos de Newton, fue precisamente resolver la última de esas preguntas. Volveremos a este asunto en un capítulo posterior.
Un poco de historia: Hooke y el postulado de gravitación. Si bien Newton es recordado por ser el padre intelectual de la teoría de gravitación universal, una de sus contribuciones fundamentales a la física y el punto de partida de la mecánica celeste moderna, la idea de que el movimiento de los planetas se debía a una fuerza dirigida hacia el Sol (no hacia adelante en sus órbitas, como habían propuesto Kepler y Descartes) fue presentada por primera vez ante la Royal Society por Robert Hooke ("huk", ver Figura (hooke)).
En 1666 (el mismo año en el que un Newton de 22 años, recién graduado, comenzaba sus propias reflexiones sobre el fenómeno gravitacional sin comunicarselo a nadie), Hooke escribió:
"Explicaré un sistema del mundo que difiere en muchos particulares de cualquier otro conocido hasta ahora [...] Este sistema depende de tres supuestos. Primero, que todos los cuerpos celestes posean un poder atractivo o gravitatorio hacia sus propios centros, de modo que no tan solo a sus partes, impidiendo que se alejen de ellos, como observamos hace la Tierra, sino que también atraigan a todos los demás cuerpos celestes que hallen dentro de su zona de actividad [...] La segunda suposición es que todos los cuerpos que son puestos en movimiento simple y directo continúen moviéndose hacia delante en una línea recta, hasta que se encuentre con alguna otra fuerza efective que los desvíe e incline en un movimiento que describa un círculo, una elipse o cualquier otra línea curva compuesta. La tercera suposición es que esas fuerzas de atracción sean tanto más poderosas en su acción cuanto el cuerpo que debe snetri su influencia se halle más cerca de su centro." (Christianson, 1984)
Como puede leerse en este extracto, en los escritos de Hooke, que a diferencia de Newton no desarrollo mucho más allá de esta sencilla formulación, estaba la semilla no solo de la idea de la gravedad, sino que también se presentaba una versión de la ley de inercia y el principio de disminución de la intensidad gravitacional con la distancia. Más adelante Hooke iría más lejos y propondría que la intensidad de la fuerza disminuía específicamente con el cuadrado del inverso de la distancia, en una carta dirigida a Newto y fechada en enero de 1680.
Después de que Newton presentará en sus escritos de esa misma década de 1680, incluyendo los Principia, su postulado de gravitación universal, comenzó con Hooke una penosa disputa de prioridad. Hooke acuso a Newton hasta su muerte de haberle robado las ideas de la gravitación universal y Newton despreció profundamente Hooke por sugerir que su contribución más grande a la historia de la ciencia había sido copiada de otro. Hoy la historia le reconoce a Hooke su prioridad (o al menos simultaneidad) en dos ideas: la idea de la atracción universal (que concibió simultaneamente e independeintemente con Newton) y la idea (planteada como una hipótesis sin demostración matemática) de que los cuerpos sometidos a una fuerza gravitacional se mueven sobre elipses, un asunto sobre el que volveremos en el Capítulo El problema de los dos cuerpos.
5.3.11. El campo gravitacional¶
Otra forma de escribir el postulado de gravitación, es reconcer que la fuerza gravitacional que produce una partícula de masa $M$ sobre cualquier otra partícula de masa $m$ situada en un punto arbitrario con posición relativa $\vec r$ (donde $\vec r$ es el vector que va de la posición de $M$ a la del punto arbitratio) es:
\begin{equation} \label{eq:fuerza_M_m} \vec F=m\left(-\frac{GM}{r^3}{\vec r}\right) \end{equation}De aquí podemos postular que el campo vectorial:
\begin{equation} \label{eq:campo_gravitacional} \vec g\equiv-\frac{GM}{r^3}{\vec r}, \end{equation}existe independiente de si hay una masa $m$ que pueda sentirlo. A esta cantidad vectorial (¿entidad física?) la llamaremos en lo sucesivo el campo gravitacional producido por la partícula puntual $M$.
En términos del campo gravitacional, la fuerza que experimenta una partícula de prueba situada en $\vec r$ respecto a $M$ se escribe:
\begin{equation} \label{eq:fuerza_campo_gravitacional} \vec F=m\vec g \end{equation}Esta última relación esta lejos de ser trivial. En realidad la extenderemos para denotar, de manera general, la fuerza gravitacional experimentada por una partícula en un campo gravitacional $\vec g$, independientemente de si el campo es producido por una partícula puntual, por un sistema de partículas, un cuerpo rígido o un fluído.
5.3.12. Energía potencial gravitacional¶
Es posible demostrar (ver problemas al final de este capítulo) que la fuerza gravitacional de la Ec. (fuerza_M_m), es una fuerza conservativa con función de energía potencial igual a:
\begin{equation} \label{eq:energia_potencial_gravitacional} U=-\frac{G M m}{r}, \end{equation}Nota: Energía potencial gravitacional negativa. En términos rigurosos la función de energía potencial más general de la que podemos derivar la fuerza gravitacional es
$$U=-\frac{GMm}{r}+C$$siendo $C$ una constante arbitraria. Esta libertad implica que el valor de la energía gravitacional no tiene en realidad un significado físico relevante. Lo importante en la dinámica es la diferencia de energía potencial entre dos puntos del espacio $\Delta U$ y que determina, por ejemplo, el cambio en la energía cinética a través de la Ec. (deltaU_deltaK.) Naturalmente para el cáluclo de $\Delta U$ el valor de $C$ es irrelevante.
La elección arbitraria de $C=0$ que hicimos al escribir la Ec. (energia_potencial_gravitacional), sin embargo, tiene una interpretación interesante, que podemos obtener al aplicar la conservación de la energía $\Delta K=-\Delta U$ en una situación hipotética.
Imaginemos que cuando dos partículas están a una distancia $r$ finita, su energía cinética total es 0 (están en reposo relativo) y su energía potencial $U_0<0$. Por efecto de la acción instantánea de un agente externo, una de las partículas se acelera (el sistema recibe una inyección de energía mecánica $\Delta E>0$) hasta que las dos partículas terminan separadadas a una distancia enorme $r\rightarrow \infty$ donde su velocidad vuelve a ser casi nula $v\rightarrow 0$ (podría ser mayor, pero asumiremos este caso extremo).
A esa distancia, el sistema tiene energía cinética total $K\rightarrow0$ y dado que $C=0$, su energía potencial será también $U\rightarrow 0$. Aplicando la conservación de la energía mecánica total:
$$ \begin{array}{rcl} \Delta K & = & -\Delta U\\ 0-(0+\Delta E) & = & -(0-U_0)\\ \Delta E & = & -U_0 \end{array} $$En conclusión: El valor absoluto de la energía potencial $U_0$ se puede interpretar como la energía mecánica adicional que necesita un sistema para apenas escapar de su mutua interacción gravitacional.
En otros términos, el signo negativo de la energía potencial podría interpretarse no solamente como una elección arbitraria de una constante matemática sino también como una deuda energética, es decir como la energía que debe aportar un agente externo para liberar a las partículas de su "esclavitud" gravitacional.
Dado que la energía potencial de cualquier partícula, sometida a la fuerza gravitacional de $M$ es proporcional a su masa $m$, es posible definir la función de potencial gravitacional o simplemente el potencial gravitacional:
\begin{equation} \label{eq:campo_gravitacional} V \equiv \frac{U}{m} = -\frac{GM}{r} \end{equation}$V$ es un campo escalar (de acuerdo a las definiciones de la Sección Funciones) y como sucede con el campo vectorial $\vec g$, en muchas aplicaciones es la representación matemática del campo gravitacional producido por una partícula.
Una última relación interesante que resulta de comparar la Ec. (energia_fuerza_campo_gravitacional) con la Ec. (fuerza_campo_gravitacional) es la siguiente:
\begin{equation} \label{eq:potencial_campo_gravitacional} \vec g = -\partial_{\vec r} V \end{equation}que es análoga a la definición de $U$ (ver Ec. funcion_energia_potencial), $\vec F=-\partial_{\vec r} U$.
5.3.13. Masa y principio de equivalencia¶
La masa, como aparece en la Ec. (campo_gravitacional), es tanto una medida de las capacidad de un cuerpo para producir campo gravitacional (y afectar a otras partículas), o, como se expresa en fuerza_campo_gravitacional, una medida de su "sensibilidad" al campo gravitacional producido por otros cuerpos $^3$.
La masa, así concebida, es muy diferente, conceptualmente, a la que usamos (y uso Newton originalmente) para definir las cantidades dinámicas en la Sección Cantidades dinámicas. Por ello es necesario precisar la diferencia entre esos dos tipos de masa con una definición:
Definición 11.8. Masa inercial y masa gravitacional. En mecánica Newtoniana distinguimos dos tipos de masa conceptualmente diferentes:
Llamamos masa inercial m_I a la razón entre las magnitudes del momento lineal de una partícula y su velocidad, a saber $m_I=p/v$. La masa inercial de una partícula es la que aparece en la ecuación de movimiento $\ddot{\vec{r}}=\vec F/m_I$ y en la energía cinética $K=m_I v^2/2$.
Por otro lado la masa gravitacional $m_G$ es la masa que determina la intensidad del campo gravitacional producido por una partícula $V=G m_G/r$ (masa gravitacional activa) o la intensidad de la fuerza que ella experimenta en un campo gravitacional de otro cuerpo, $\vec F=m_G\vec g$ (masa gravitacional pasiva).
Si usamos el postulado de fuerza (Ec. edm_fuerza_aplicadas) y la expresión para la fuerza gravitacional escrita en la Ec. (fuerza_campo_gravitacional), encontramos que la aceleración que sufre una partícula de masa inercial $m_I$ y masa gravitacional (pasiva) $m_G$ en un campo gravitacional $\vec g$ es:
\begin{equation} \label{eq:razon_masa_gravitacional_masa_inercial} \ddot{\vec r}=\frac{m_G}{m_I}\vec g \end{equation}La razón $m_G/m_I$, ha sido medida cuidadosamente en el laboratorio desde finales del siglo 1500 (ver recuadro Un poco de historia: El experimento de Eötvos), con un resultado ampliamente conocido: el valor numérico de la masa gravitacional (pasiva) coincide con el de la masa inercial hasta la onceava cifra significativa (Roll1 et al., 1964).
La igualdad entre la masa gravitacional e inercial ha sido elevada hoy a la altura de un principio fundamental de la mecánica, el principio de equivalencia:
Principio: Principio de equivalencia (versión débil). $^4$. La aceleración de de una partícula puntual en un campo gravitacional depende únicamente del valor del campo y es independiente de la masa y composición de la partícula. En términos matemáticos, en la mecánica newtoniana, $m_G=m_I$.
Por la igualdad numérica (mas no conceptual) entre la masa gravitacional (pasiva) y la mas inercial, en el contexto de la mecánica newtoniana, usaremos en lo sucesivo el símbolo $m$ para referirnos a la masa sin distinguir si se trata de la una o la otra.
Un poco de historia: El experimento de Eötvos. La pregunta de sí dos cuerpos de distinta masa caen al mismo tiempo cuando son lanzadas desde la misma altura (que, en términos modernos, es igual a la pregunta de si tienen la misma aceleración), ha ocupado a pensadores desde la antigüedad.
El primer experimento preciso de este tipo fue realizado por Simon Stevin (1548-1620, ver Figura (stevin)), un matemático, filósofo e ingeniero flamenco (es decir de la región que hoy llamamos Bélgica) que hizo importantes contribuciones tempranas a la mecánica prenewtoniana.
En 1586, Stevin lanzó dos esferas de acero que tenían una masa diferente por un factor de 10, desde una altura de aproximadamente 10 metros. Registro la diferencia en el tiempo de caída escuchando el golpe que hacían las esferas al golpear el suelo (Devreese, 2008). El resultado fue contundente: las dos esferas caían casi exactamente al mismo tiempo (al menos dentro de la sensibilidad del experimento.)
Posteriormente Galileo (quien citaría a Stevin en sus libros) realizó comprobaciones similares usando planos inclinados $^5$. Newton y Bessel intentaron resolver también la cuestión, esta vez usando péndulos (el período de un péndulo depende también de la aceleración que sufre el cuerpo) con resultados similares a Stevin: todos los cuerpos sin importar su masa y composición, tienen la misma aceleración en el campo gravitacional de la Tierra. En términos de la Ec. (razon_masa_gravitacional_masa_inercial), $m_G/m_I=1$.
Las medidas más precisas de la razón entre las masas gravitacional e inercial fueron realizadas entre 1889 y 1909 por el físico húngaro Roland von Eötvos ("fon otfosh") y sus colaboradores, usando para ello un instrumento conocido como la balanza de torsión (similar al usado para medir la constante de gravitación universal.) Los experimentos probaron la igualdad entre la masa gravitacional y la masa inercial hasta la octava cifra significativa y fueron repetidos en la segunda mitad de los 1900 hasta alcanzar la precisión mencionada en el texto: once dígitos significativos (Roll et al., 1964).
NOTAS AL PIE:
- La copia digital de una primera edición del libro puede leerse en línea en la biblioteca digital de la Universidad de Cambridge http://cudl.lib.cam.ac.uk/view/PR-ADV-B-00039-00001/1
- El intervalo es cerrado en $t_1$ en tanto en algún momento tiene que comenzar la condición de movimiento libre de fuerzas, mientras que es abierto en $t_2$ en tanto esa condición podría extenderse para siempre
- En términos estrictos, la masa que produce el campo y la masa que lo siente, deberían diferenciarse también. La primera sería una masa gravitacional activa y la segunda una masa gravitacional pasiva. En lo que sigue nos ocuparemos únicamente de la masa gravitacional pasiva, o para acortar, la masa gravitacional.
- El adjetivo débil, hace referencia al hecho de que existe un principio de equivalencia más fundamental sobre el que se sustenta la teoría de la relatividad general.
- La idea de que Galileo realizó un experimento similar al de Stevin, lanzando objetos desde lo alto de la Torre de Pisa no ha podido ser confirmado y podría tratarse de una anécdota apócrifa.
Indice | Previo: Mecanica.Dinamica.Cantidades | Siguiente: Mecanica.Dinamica.SistemaParticulas