Indice | Previo: ProblemaNCuerpos | Siguiente: ProblemaNCuerpos.SolucionAnalitica

6.1. Formulación del problema

6.1.1. Motivación

El problema de los N cuerpos es uno de los más importantes problemas de la Física y, posiblemente, el primer problema de física teórica que se formuló en la historia de esta disciplina.

Cuando Newton desarrollo su teoría mecánica con el propósito de describir el movimiento de los cuerpos del Sistema Solar, era claro que en el sistema existían cuerpos que dominaban el movimiento de otros, sin verse significativamente afectados por ellos.

Así por ejemplo, el Sol domina el movimiento de la Tierra, Júpiter por su lado domina el movimiento de sus lunas, mientras que Saturno lo hace para el movimiento de las partículas que componen sus anillos.

Cuando un cuerpo domina el movimiento de muchos otros cuerpos ligeros (el Sol y los asteroides, Júpiter y sus Lunas, etc.) predecir los movimientos en el sistema es relativamente sencillo: la fuerza que ejercé el cuerpo principal sobre cada cuerpo pequeño se puede considerar independiente de la posición o velocidad de todos los demás. En este caso, la solución al problema se obtiene resolviendo, independientemente, la ecuación de movimiento de cada uno de los cuerpos en el sistema (como veremos en el Capítulo El problema de los dos cuerpos).

Al estudiar, sin embargo, la dinámica de algunos sistemas gravitacionales en el Universo en los que no existe necesariamente un cuerpo dominante, tales como un cúmulo de estrellas o galaxias, el sistema formado por el Sol y los planetas (aunque el Sol es 1000 veces más masivo que el planeta más grande, al calcular de forma muy precisa la posición de los planetas para hacer observaciones o enviar naves espaciales, es necesario considerarlo un cuerpo más en el sistema), el sistema formado por Plutón y sus satélites (especialmente Caronte), etc., se hace claro que la dinámica de estos sistema es mucho más compleja que aquella que se predice usando la aproximación mencionada en el párrafo anterior.

Cuando se admite que en un sistema de muchas partículas, la posición y velocidad de todas ellas debe considerarse para obtener una descripción correcta de la dinámica del sistema, decimos que nos enfrentamos al problema de los N cuerpos $^1$

6.1.2. Enunciado físico y matemático

Definición 11.9. Problema de los N cuerpos. "Dado un sistema con un número arbitrario de partículas puntuales que se atráen mutuamente obedeciendo [los postulados mecánicos] de Newton, encontrar, bajo la suposición de que ninguna de esas partículas colisiona, una representación de las coordenadas de cada partícula como una serie de una variable que sea una función conocida del tiempo, tal que para todos los valores de la variable, la serie converga uniformemente. " $^2$

Figura 6.63. El problema de los N cuerpos: dadas las condiciones iniciales de un conjunto de N partículas puntuales, predecir la posición y velocidad de las partículas en cualquier instante futuro.

Esta formulación del problema, que tiene un marcado estilo matemático, puede matizirse con algunos comentarios físicos:

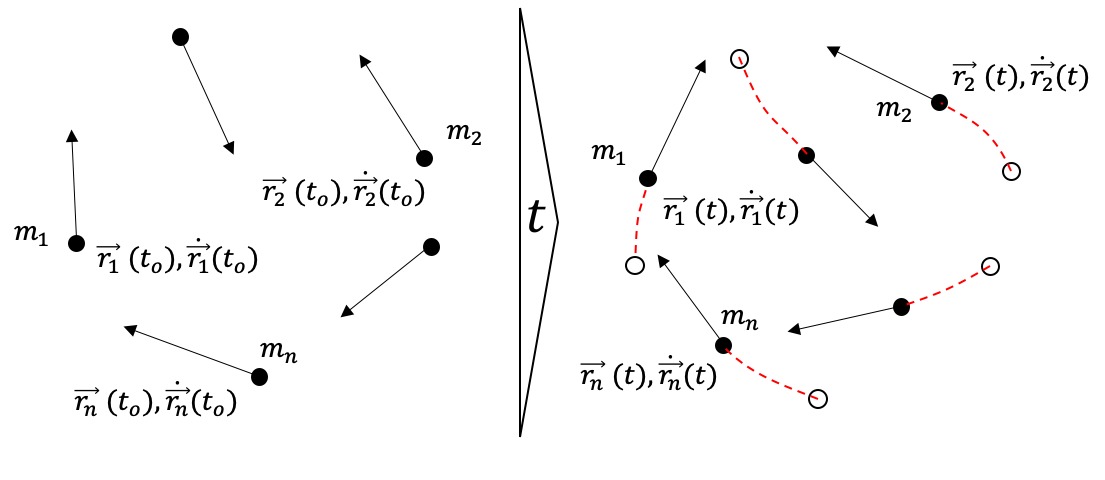
• Asumimos que en un momento dado del tiempo $t_0$, las posiciones y velocidades de todas las partículas (condiciones iniciales) son conocidas $\{{\vec r_i(t_0)},{\dot{\vec r}_i(t_0)}\}_{N}$ (ver Figura (ncuerpos_formulacion).) Adicionalmente suponemos que las posiciones de dos o más partículas no coinciden completamente en el tiempo inicial $t_0$. El problema de los N cuerpos consiste entonces en encontrar las posiciones y velocidades de todas las partículas en un instante futuro de tiempo $t$, es decir encontrar $\{{\vec r_i(t)},{\dot{\vec r}_i(t)}\}_{N}$ .

• Al decir que la solución puede, en general, expresarse como una serie de una variable dependiente del tiempo (no necesariamente el tiempo mismo), el enunciado admité que no es necesario que las posiciones y velocidades deban expresarse en la forma de funciones analíticas (p.e. polinomios, funciones trigonométricas, función logarítmica o exponencial, etc.) Es claro que, al menos para propósitos del cálculo aproximado de la solución, tener una serie convergente puede ser tan útil como tener una solución analítica (aunque naturalmente no es lo mismo, especialmente si la serie converge muy lentamente como veremos más adelante.)

• La convergencia uniforme es una condición matemática rigurosa, aplicada a las sucesiones y series, que implica, en pocas palabras que las posiciones y velocidades calculadas con la serie sean tan cercanas como se desee a las posiciones y velocidades reales, sin importar el tiempo en el que se calculen.

• Como lo admite implícitamente el enunciado, no se espera que sea posible predecir el estado del sistema en cualquier instante futuro. En el caso, por ejemplo, en el que las condiciones iniciales conduzcan a una colisión, es decir, una situación en la que al menos dos partículas en el sistema podrían situarse a una distancia nula una de otra, se produciría una singularidad matemática en el sistema (fuerzas infinitas). Aún en casos en los que se produzcan colisiones, se espera que sea posible predecir la evolución del sistema entre el tiempo inicial y el tiempo de la primera colisión.

Matemáticamente, el problema de los N cuerpos es equivalente la solución de las e.d.m. de todas las partículas (Ecs. edm_sistema):

$$ \left\{\ddot{\vec r}_i=\frac{1}{m_i}\sum_{j\neq i} \vec F_{ij}\right\}_{N}, $$

donde no sobra recordar que según las convenciones usadas aquí, $\vec F_{ij}$ es la fuerza ejercida sobre la partícula $i$ por la partícula $j$.

Como esta implícito aquí, asumiremos que no existe ninguna fuerza externas sobre las partículas del sistema, p.e. fricción con un medio, interacción con un campo externo, etc.

De acuerdo a la formulación del problema presentada en la Definición edm_sistema, asumimos que la dinámica es estrictamente newtoniana, lo que incluye suponer que la única interacción a distancia entre las partículas es la interacción gravitacional newtoniana (ver Pos. \ref{pos:gravitacion.universal}, Ec. fuerza_gravitacional):

$$ \vec{F}_{ij} = -\frac{Gm_i m_j}{r_{ij}^3} \vec r_{ij}. $$

donde tampoco sobra recordar que en lo sucesivo el vector relativo $\vec{r}_{ij}\equiv\vec{r}_i - \vec{r}_j$ apunta en la dirección que va de la partícula que produce la fuerza (partícula $j$) hacia la partícula que la experimenta (partícula $i$).

En términos explícitos, finalemente, el problema de los N cuerpos en mecánica celeste, consiste en resolver el conjunto de ecuaciones diferenciales:

\begin{equation} \label{eq:ncuerpos_formulacion_ecuaciones} \left\{\ddot{\vec r}_i= -\sum_{j\neq i} \frac{\mu_j}{r_{ij}^3} \vec{r}_{ij} \right\}_{N}, \end{equation}

donde hemos introducido el parámetro gravitacional $\mu_j\equiv G m_j$ sobre el que volveremos en la Sección *Solución numérica del problema de los N cuerpos.

Un poco de historia: Henri Poincaré y el premio del Rey Oscar. En 1889, el matemático sueco Mittag-Leffer convenció al rey Oscar II de Suecia de que, con motivo de la celebración de su cumpleaños presentará al mundo un nuevo concurso matemático.

Entre los problemas formulados en el concurso del rey Oscar II se encontraba, precisamente, el problema de los N cuerpos. La formulación del problema presentada en este capítulo, es literalmente la que preparó para el Rey, el matemático alemán Karl Weierstrass ("Vierstrass"), inspirado originalmente por las ideas del también matemático alemán Peter Gustav Dirichlet ("Diriclet").

Uno de los participantes del concurso, fue el matemático Francés Henri Poincaré ("Honri Poancaré") , que contaba para la época con 35 años (ver Figura (henri_poincare)).

Poincaré nació en Francia el 29 de abril de 1854 y se graduo como doctor en matemáticas en 1879 bajo la orientación de Charles Hermite ("Charle ermit").

Las mayores contribuciones de Poincaré, como matemático, se produjeron en la teoría de ecuaciones diferenciales. Sin embargo, por sus estudios posteriores de ingeniería, su posición como profesor de la Universidad de Paris (La Sorbona) en las áreas de Mecánica, Física Matemática, Teoría de la Probabilidad, Mecánica Celeste y Astronomía, además del reconocimiento público que lo llevo a ser miembro de la Oficina de Longitudes de Francia en 1897 y elegido presidente de la Academia Francesa de Ciencias en 1906, los conocimientos de Poincaré se extendieron a muchas otras disciplinas. De allí que sea considerado un Polímata o un "hombre universal" (alguien que domina muchas disciplinas intelectuales o artísticas) un apelativo que comparte con personajes como Aristóteles o Leonardo da Vinci).

El artículo presentado por Poincaré en el concurso del Rey Oscar II, titulado "Sobre el problema de los tres cuerpos y las ecuaciones de la dinámica"(Poincare, 1890), fue declarado, sin lugar a dudas el ganador del concurso. Pero mo sin alguna polémica. De un lado el trabajo no resolvía el porblema general y del otro contenía algunos errores que fueron solo corregidos después. Adicionalmente la "solución" cuya existencia demostraba Poincaré suponía que los cuerpos se mantendrían siempre a una distancia mayor a un cierto valor mínimo. El mismo Poincaré admitiría, que la solución general al problema tal vez no se encontraría pronto y que serían necesarias "herramientas analíticas infinitamente más complicadas que las disponibles en la época." Aún así los métodos introducidos por Poincaré en aquel trabajo de 1890, influenciarían de forma importante la mecánica celeste y serían la base para el desarrollo de la teoría del caos.

El problema de los tres cuerpos, formulado a la manera del concurso del rey Oscar II, fue finalmente resuelto en 1912 por el matemático Finlandés Karl Sundman Sundman, 1913. En este trabajo Sundman probó la existencia de series que describían la posición de los tres cuerpos y que convergían para tiempos arbitrarios. Una excelente síntesis histórica de la contribución (poco apreciada) de Sundman puede encontrarse en Barrow-Green, 2010.

Figura 6.64. Fotografía de Henri Poincaré hacia el año 1886, unos años antes de realizar su trabajo histórico sobre el problema de los tres cuerpos (Foto: Eugène Pirou)

NOTAS AL PIE:

1. En otras áreas de la física, a este problema se lo conoce también como el problema de muchos cuerpos y en general no se restringe únicamente a describir el movimiento del sistema (que es propio de la física clásica), sino también, por ejemplo, su estado cuántico y posible evolución en el tiempo.

2. Tomado literalmente del prefacio del editor en Poincare, 1992, que a su vez reproduce el texto del concurso organizado por el rey de Suecia Oscar II en 1889 (ver el recuadro Un poco de historia en esta sección).

Indice | Previo: ProblemaNCuerpos | Siguiente: ProblemaNCuerpos.SolucionAnalitica