Indice | Previo: FormalismoLagrangiano | Siguiente: FormalismoLagrangiano.VariablesRestricciones

9.1. Motivación

La teoría desarrollada hasta este punto en el texto se basa en el denominado formalismo vectorial de la mecánica, que basicamente expresa toda la dinámica de los sistemas de partículas usando cantidades vectoriales y sus relaciones matemáticas y geométricas.

En este formalismo la solución a cualquier problema mecánico que requiera predecir la posición de un sistema de partículas, requiere resolver las ecuaciones de movimiento de todas las partículas:

$$ \{\ddot{\vec{r_i}}=\vec F_i(t,\{\vec r_j\}_N,\{\vec r_j\}_N)\}_N $$

Esta aproximación a los problemas mecánicaos enfrenta una serie de limitaciones, algunas bastante obvias y otras muy sutiles. Así por ejemplo:

1. Para resolver el problema es necesario especificar completamente todas las fuerzas involucradas $\vec F_i(t,\{\vec r_j\}_N,\{\vec r_j\}_N)$, algunas de las cuales pueden ser funciones muy complejas del tiempo y de las posiciones de todas o algunas de las partículas.

1. Existen situaciones en física en donde no es posible, incluso por principio, encontrar fuerzas asociadas a las interacciones. Este es el caso por ejemplo de la teoría general de la relatividad, en el que el concepto de fuerza es accesorio y no intrínseco a la teoría, o en el caso de la aun más original teoría cuántica. En estas situaciones describir la dinámica usando la ecuación anterior es sino muy complicado, enteramente imposible.

1. El uso de cantidades vectoriales produce claramente una mayor complejidad matemática y computacional. Es posible que la notación sea más compacta pero el problema es en el fondo más elaborado y complejo.

Las limitaciones más profundas del formalismo vectorial residen en la incapacidad que tiene para revelar propiedades no triviales de los sistemas dinámicos, como descubriremos más adelante. En este capítulo, presentaremos una reformulación nueva de la mecánica, partiendo de novedosos (y más generales) principios fundamentales. El nuevo formalismo tiene además una estructura matemática que en principio es más fácil de manejar en tanto se basa enteramente en cantidades escalares. Llamamos a esta formulación nueva, en general, un formalismo escalar de la mecánica.

El formalismo escalar no solamente ha sido exitosamente aplicado en los últimos 250 años para resolver todos los problemas conocidos de la mecánica, incluyendo naturalmente los problemas de la mecánica celeste, sino que además ha probado ser increíblemente poderoso en la descripción de fenómenos en áreas diferentes como la electricidad y el magnetismo, la relatividad general y la mecánica cuántica. No sería exagerado decir que el formalismo escalar de la mecánica fue posiblemente uno de los descubrimientos teóricos más importantes en la historia de la física.

Es interesante anotar que si bien la mecánica Newtoniana hoy se considera tan solo una teoría efectiva, es decir, conceptualmente imprecisa y que fue reemplazada por la Teoría de la Relatividadm, una teoría más fundamental del espacio-tiempo y el movimiento, el formalismo escalar que se desarrollo en el tiempo en el que la mecánica newtoniana estaba en la cúspide, sigue estando hoy en la base de las teorías física modernas no newtonianas, incluyendo la teoría de la relatividad.

Si bien la mayoría de los problemas que resolveremos en este capítulo, aplicando este nuevo formalismo, ya los resolvimos usando el formalismo vectorial, veremos como sus principios y las herramientas derivadas permiten entender aspectos de los problemas que en el formalismo vectorial toma tiempo entender, e incluso resolver más fácil problemas que no hemos abordado todavía.

9.2. El formalismo Lagrangiano

El primer formalismo escalar de la mecánica fue presentado en el año 1788 por el matemático y astrónomo italo-francés Joseph-Louis Lagrange (del que ya habíamos hablado en la Sección Los puntos de equilibrio del CRTBP. Este formalismo ofrecía una serie de importantes ventajas frente a la formulación Newtoniana ampliamente conocida en su época. A esta nueva presentación de la mecánica se la conoce hoy como el formalismo Lagrangiano.

El formalismo Lagrangiano se basa originalmente en una ingeniosa y poderosa herramienta teórica ideada originalmente por el físico y matemático francés Jean le Rond d'Alembert ("yan le ron dalambert"). D'Alambert desarrollo esta idea para resolver específicamente problemas en los que una partícula o un conjunto de partículas se encuentran en equilibrio mecánico. En el formalismo vectorial de la mecánica, el equilibrio se expresa como una condición en el que la fuerza y la torca neta que actúa sobre cada partícula en el sistema es nula. La idea de d'Alambert fue utilizar, en lugar de la fuerza y la torca, el concepto de trabajo.

9.2.1. Principio de los trabajos virtuales

Para d'Alembert otra forma de expresar el equilibrio es la siguiente: supongamos que tomamos cada partícula del sistema en equilibrio y las desplazamos de sus posiciones, y de forma imaginaria (desplazamientos virtuales), en cantidades infinitesimalmente pequeñas, $\{\delta \vec r_i\}$$^1$.

Si los desplazamientos de las partículas satisfacen las restricciones internas del sistema, entonces, postula d'Alambert, la suma del trabajo realizado por todas las fuerzas que actúan sobre las partículas será nulo. A esta idea se la conoce como el principio de los trabajos virtuales y es de amplió uso en el estudio de sistemas de partículas en equilibrio en partícular aquellas que forman cuerpos rígidos.

En términos matemáticos el principio de los trabajos virtuales puede escribirse como:

\begin{equation} \sum_i \vec{F_i}\cdot\delta\vec r_i=0 \end{equation}

En la Figura (trabajos_virtuales) se presenta un sencillo problema de mecánica con el que podemos ilustrar el uso del principio de los trabajos virtuales.

Figura 9.144. Arriba: una barra de peso $W$ (conocido) se encuentra apoyada sobre un pivote (triángulo) mientra se aplica sobre ella sendas fuerzas $

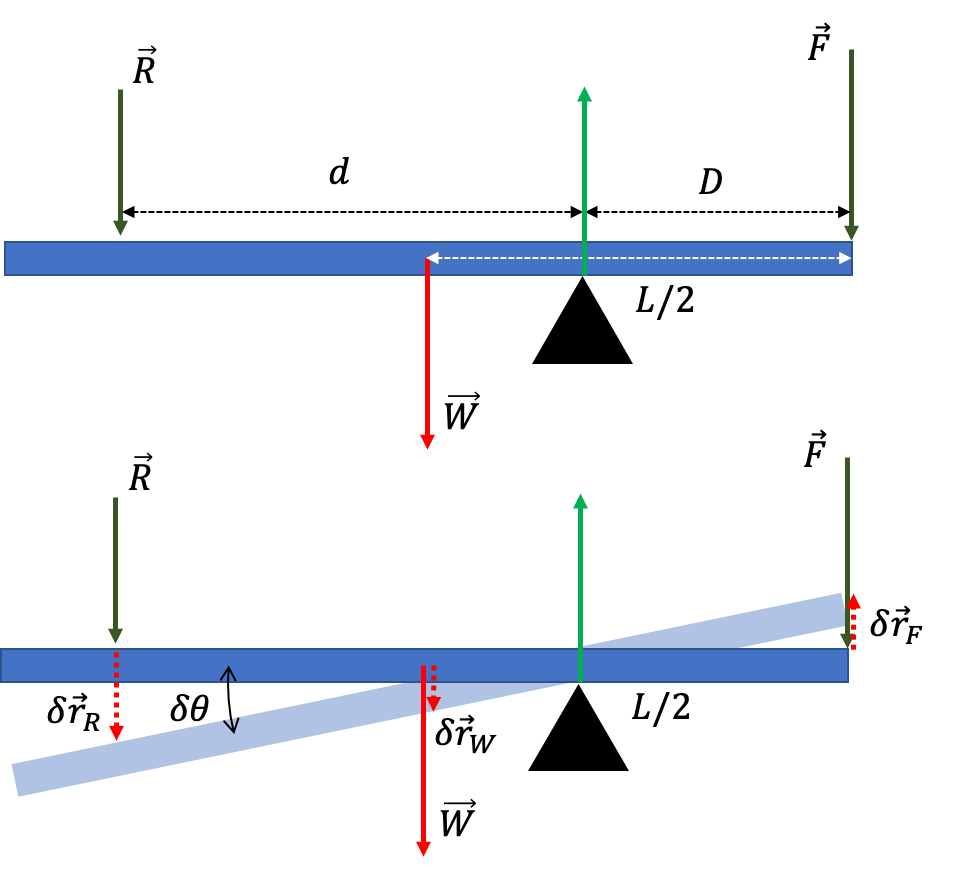
Queremos resolver en este problema la pregunta de cuál es la magnitud de la fuerza $\vec R$ que debo aplicar sobre la barra para que el sistema este en equilibrio. Si bien este es un problema relativamente trivial de estática newtoniana, lo resolveremos usando, justamente, el principio de los trabajos virtuales de D'Alambert.

Para ellos podemo desplazar de forma imaginaria, todas las partes de la barra manteniendo, eso sí, su forma y longitud (restricciones internas). El desplazamiento puede realizarse en cualquier dirección y de cualquier manera (siempre que se cumplan las restriccion), pero evidentemente existirán unos desplazamientos en los que el principio pueda usarse de forma más útil. Así por ejemplo, el desplazamiento virtual mostrado en la Figura (trabajos_virtuales) será a todas luces el más útil.

Dadas las restricciones impuestas por la rigidez de la barra, los desplazamientos virtuales asociados a las fuerzas pueden expresarse como función del ángulo virtual $\delta\theta$ en el que la hacemos girar, en la forma:

\begin{eqnarray} \delta r_R & = & -d \delta \theta\\ \delta r_W & = & -(L/2-D) \delta \theta\\ \delta r_F & = & +D \delta \theta\\ \delta r_N & = & 0\\ \end{eqnarray}

El principio de los trabajos virtuales, Ec. (trabajos_virtuales, puede escribirse en este caso como:

$$ -Rd\delta\theta-W(L/2-D)\delta\theta+FD\delta\theta=0 $$

Dado que el desplazamiento $\delta\theta$ es arbitrario, esta igualdad es equivalente a:

$$ -Rd-W(L/2-D)+FD=0 $$

Y de allí puede obtenerse el valor de la magnitud de la fuerza necesaria:

$$ R=\frac{FD-W(L/2-D)}{d} $$

Si bien este problema parece trivial, debe anotarse que en ningún momento recurrimos a los principios de la mecánica Newtoniana, es decir al postulado de fuerzas o al teorema de acción y reacción, para resolver el problema. Esto ilustra claramente como esta forma de aproximarse a su solución ma es realmente una alternativa nueva a estas leyes.

Otro elemento novedoso de esta aproximación, es la manera como quedan excluidas, de forma natural, fuerzas que son mucho más difíciles de modelar, tales como las fuerzas que mantienen unidas las partes del cuerpo o las fuerzas que resultan de la interacción de este con su entorno (por ejemplo la fuerza $N$).

9.2.2. Principio de d'Alambert-Lagrange

¿Podríamos aplicar un principio parecido a este pero en el caso de un sistema en movimiento?. Esta fue justamente la pregunta que intentaron resolver D'Alambert y luego Lagrange para generalizar el principio de los trabajos virtuales a todos los problemas de la mecánica.

Considere por ejemplo el mismo ejemplo anterior pero en una situación en la que la barra ya no esta en equilibrio. En su lugar rota con aceleración angular $\alpha$ en dirección contraria a las manecillas del reloj. En esta situación, sabemos que incluso si $F$ se hace cero, un valor de $R$ positivo podría ser consistente con la condición dinámica sel sistema, lo que ciertamente contradice la solución encontrada con el principio de los trabajos virtuales.

Para resolver la situación D'Alambert y Lagrange formulan el siguiente principio general:

Principio: Principio de d'Alambert-Lagrange. En un sistema de N partículas sometidas a fuerzas $\{\vec{F}_i\}_N$ el trabajo virtual total realizado por las fuerzas efectivas. $\{\vec{F}_i-\dot{\vec{p}_i}\}_N$ es igual a cero:

\begin{equation} \label{eq:teorema_dalambert_lagrange} \sum_i (\vec{F_i}-\dot{\vec{p}_i})\cdot\delta\vec r_i=0 \end{equation}

Como cualquier principio de la física el principio de D'Alambert-Lagrange no tienen ninguna justificación. Supone una relación inesperada, nueva, entre las cantidades involucradas en los problemas mecánicos. Algunos podrían encontrarlo bastante obvio, en tanto, de acuerdo con el postulado de fuerzas $\vec{F}_i=\dot{\vec{p}_i}$ y por lo tanto $\vec{F}_i-\dot{\vec{p}_i}=\vec o$. Pero no debemos olvidar que es justamente el postulado de fuerzas el que queremos reemplazar en esta reformulación de la mecánica.

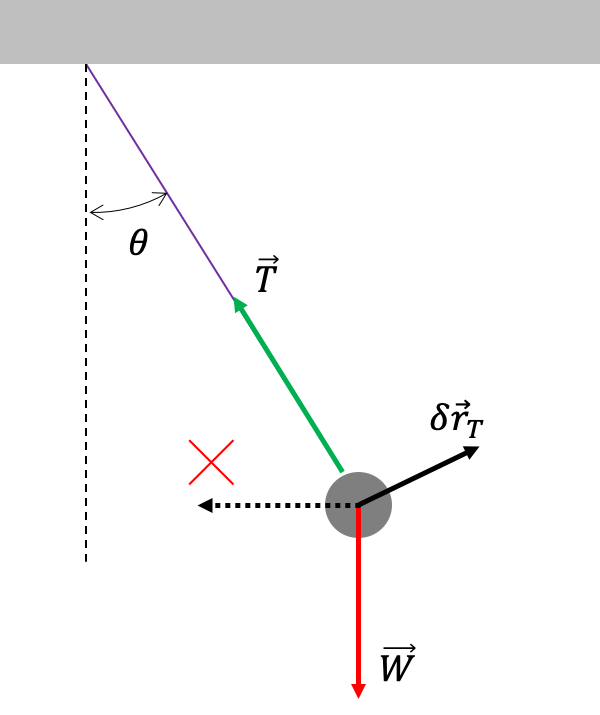
Para ilustrar de qué manera el principio de d'Alambert-Lagrange constituye una alternativa nueva para la solución de problemas mecánicos, consideremos otro problema bien conocido: el péndulo simple. En la Figura (pendulo_simple_dAlambert) se ilustra esquemáticamente las condiciones básicas del problema.

Figura 9.145. Una partícula puntual de peso $

Para aplicar el principo de d'Alambert-Lagrange, debemos primero encontrar un desplazamiento virtual que sea compatible con las restricciones del problema. El desplazamiento horizontal $\delta \vec{r}_H$ por ejemplo no es aceptable: si la partícula se mueve (imaginariamente) en esa dirección, la cuerda que la sostiene se distendería (también imaginariamente) violando una de las restricciones del problema. Tampoco sirve un desplazamiento virtual saliendo del plano del péndulo: se supone que el movimiento de la partícula solo puede realizarse sobre dicho plano. El único desplazamiento virtual compatible, es uno que se realice en dirección perpendicular a la cuerda, o bien en el sentido del movimiento o en sentido contrario (la aplicación del principio no depende estrictamente del sentido elegido).

Después de este deplazamiento virtual, el trabajo total realizado por todas las fuerzas efectivas sobre la partícula, será:

$$ [(\vec T+\vec W)-m\dot{\vec{v}}]\cdot\delta \vec r_T=0 $$

Ahora bien, por las restricciones del problema $\vec T\cdot\delta\vec r_T=0$ y por lo tanto la tensión no aparecerá en la ecuación que rige la dinámica del sistema (solo lo hace implícitamente al restringir la manera como se puede definir el desplazamiento virtual).

En términos de la única fuerza remanente, el peso, y expresando la fuerza y el desplazamiento vitual en coordenadas cartesianas, el principio de d'Alambert-Lagrange para este sistema se puede escribir como:

\begin{equation} \label{eq:dalambert_pendulo_simple} (W_x-m \dot v_x)\delta x+(W_y-m \dot v_y)\delta y =0 \end{equation}

Lamentablemente esta ecuación es muy poco útil. Para empezar hay dos incognitas $\dot{v}_x$, $\dot{v}_y$. Peor aún, los desplazamientos $\delta x$ y $\delta y$ no son independientes. Este último, es un aspecto fundamental del nuevo principio: el sistema de coordenadas debe elegirse apropiadamente para que su aplicación sea exitosa.

Un sistema de coordenadas más apropiado, dadas las restricciones implícitas del problema, es el sistema de coordenadas polares. En este sistema la única variable independiente que describe el desplazamiento virtual del sistema, es el ángulo $\theta$. En términos de esta variable, las coordenadas cartesianas $x$, $y$ se pueden escribir como:

\begin{equation} \label{eq:xy_pendulo_simple} \begin{array}{ccc} x & = & L \sin\theta\\ y & = & -L \cos\theta\\ \end{array} \end{equation}

de modo que las componentes del desplazamiento virtual son ahora:

$$ \begin{array}{ccc} \delta x & = & L \cos\theta\delta\theta\\ \delta y & = & L \sin\theta\delta\theta\\ \end{array} $$

Por su lado, las componentes de la aceleración se pueden escribir derivando dos veces las Ecs. (xy_pendulo_simple) para obtener:

\begin{eqnarray} \dot v_x & = & -L \sin\theta \dot\theta^2 + L\cos\theta\ddot\theta\\ \dot v_y & = & L \cos\theta \dot\theta^2 + L\sin\theta\ddot\theta\\ \end{eqnarray}

Reemplazando en el principio de d'Alambert-Lagrange (Ec. dalambert_pendulo_simple) y teniendo en cuenta que $W_x=0$ y $W_y=-mg$, obtenemos:

\begin{eqnarray} \nonumber \left[-m g L \sin\theta -m (L \cos\theta \dot\theta^2 + L\sin\theta\ddot\theta)L \sin\theta\right. + & \\ \nonumber -m (-L \sin\theta \dot\theta^2 + L\cos\theta\ddot\theta)L \cos\theta & \left.\right]\delta\theta = 0 \end{eqnarray}

Dado que $\delta\theta$ es arbitrario, la ecuación anterior se puede expresar finalmente como:

\begin{equation} \label{eq:edm_pendulo_simple} \ddot\theta+\frac{g}{L}\sin\theta=0 \end{equation}

que es justamente la ecuación de movimiento del péndulo que conocíamos del formalismo vectorial.

¿Ha sido esta la manera más simple de derivar la ecuación de movimiento del péndulo simple?. ¡Ciertamente no!. ¿Ha utilizado este procedimiento algún postulado de la mecánica newtoniana original?. ¡Tampoco!. El propósito aquí no era mostrar cómo derivar esta ecuación de una forma más simple, sino ilustrar como un nuevo e independiente principio (el principio de d'Alambert-Lagrange) conduce exactamente a los mismos resultados que se pueden obtener con la aplicación del formalismo vectorial original de Newton.

Adicionalmente este ejemplo nos ha permitido adelantar algunos de los aspectos críticos de la tecnología matemática en el fondo del formalismo lagrangiano, a saber:

1. El papel de las restricciones del sistema a la hora de escoger los desplazamientos virtuales compatibles y de eliminar las fuerzas de restricción (en este caso la tensión) desde el principio de la formulación del problema.

2. La importancia de elegir un sistema de coordenadas adecuado para hacer útil la aplicación del principio.

Estos dos aspectos del formalismo lagrangiano serán justamente el contenido de la discusión en las próximas secciones.

NOTAS AL PIE:

1. el uso de "$\delta$" en lugar del tradicional "$\mathrm{d}$" del cálculo sirve para resaltar el hecho de que el desplazamiento no es real

Indice | Previo: FormalismoLagrangiano | Siguiente: FormalismoLagrangiano.VariablesRestricciones