Indice | Previo: FormalismoLagrangiano.Motivacion | Siguiente: FormalismoLagrangiano.EcuacionesLagrange
9.3. Restricciones y variables generalizadas¶
Como vimos en el ejemplo del péndulo simple, la aplicación del principio de d'Alambert-Lagrange puede ser truculenta. El número de desplazamientos virtuales consistentes con las restricciones puede ser enorme (si no infinito). No todos esos desplazamientos son compatibles con las restricciones del problema, y más sútil todavía, la manera como los podemos expresar en distintos sistemas de coordenadas, no necesariamente conducen a una ecuación útil e incluso a una ecuación soluble.
El aspecto más importante en la aplicación del principio es la elección de un conjunto apropiado de variables capaces de describir la configuración del sistema (dónde están las partículas del sistema) sin ninguna redundancia. Por ejemplo, en el caso del péndulo simple, cuando se utilizan las coordenadas cartesianas, los valores de $x$ y $y$ no son independientes. Estas dos variables están conectadas por la relación matemática:
\begin{equation} \label{eq:pendulo_restriccion_cuerda} x^2+y^2-L^2=0 \end{equation}Esta relación es una expresión de una restricción del sistema, a saber el hecho de que la cuerda es rígida. Usando esta relación es posible, si se da el valor de una de las variables ($x$ por ejemplo), obtener la otra ($y$). Es en este senrido que decimos que el sistema de coordenadas cartesianas es redundante para describir la dinámica del péndulo simple.
Con estas ideas en la cabeza podemos proceder a definir una serie de conceptos que serán fundamentales en lo que resta de la construcción del formalismo Lagrangiano.
Definición 11.13. Espacio de coordenadas. Es el espacio geométrico en el que se desarrolla la dinámica del sistema. En la física clásica, este espacio tiene tres dimensiones y por tanto la ubicación de los puntos en él se específican usando tres coordenadas por partícula. El sistema natural de coordenadas de cualquier sistema de partículas, es el sistema cartesiano.
Es importante entender que el espacio físico es el mismo para todas las partículas que constituye el sistema. Sin embargo, para especificar la configuración de N partículas 3 coordenadas no son suficientes. En realidad es necesario específicar 3N coordenadas cartesianas, que describiremos en general como $\{\vec{r}_i\}_{N}$, o equivalentemente
$$\{x^k_i\}_{3N}$$donde $x^k$ con $k:(1,2,3)$ son las coordenadas cartesianas $(x_i,y_i,z_i)$ de la partícula $i$-esima.
En el ejemplo del péndulo la Ec. (pendulo_restriccion_cuerda) es una restricción en el sentido de la definición anterior.
Definición 11.15. Restricción holonómica. Son aquellas restricciones que conectan las coordenadas cartesianas del sistema a través de una igualdad del tipo:
\begin{equation} \label{eq:restriccion_holonomica} f_k(\{\vec{r}_i\},t)=0 \end{equation}donde el índice $k$ simboliza el hecho que en un mismo problema puede existir más de una restricción.
El péndulo simple, por ejemplo, esto sometida a dos restricciones holonómicas:
$$ \begin{array}{ll} f_1(\vec r,t) & \equiv z = 0 \\ f_2(\vec r,t) & \equiv x^2+y^2-L^2 = 0 \end{array} $$Definición 11.16. Restricción no holonómica. Son aquellas restricciones que conectan las coordenadas cartesianas del sistema de una forma que no puede reducirse a la forma de una función elemental. Un caso partícular de restricciones no holonómicas son por ejemplo las restricciones que se escriben como desigualdades:
$$ f_k(\{\vec{r}_i\},t)\le 0 $$
Este tipo de restricciones son utilizadas para delimitar regiones del espacio físico a las que el sistema puede o no puede acceder. Un ejemplo de una restricción no holonómica es la que debemos aplicar, por ejemplo, si queremos describir el movimiento de las partículas de un gas contenido en una caja. En ese caso las coordenadas cartesianas pueden ser cualquiera excepto si están por fuera de la caja.
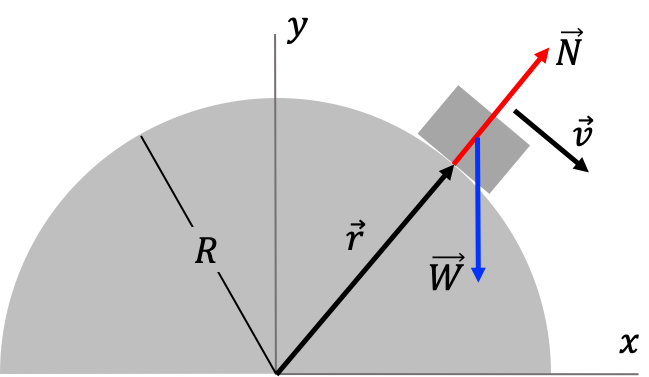
Otro tipo de restricción no holonómica se obtiene en un sistema como el mostrado en la figura abajo. Un cuerpo se mueve sobre un cascarón esférico en un campo gravitacional.
En este ejemplo, tenemos ambas, restricciones holonómicas y no holonómicas:
\begin{eqnarray} f_1(\vec r,t) & = & z = 0 \\ f_2(\vec r,t) & = & x^2+y^2-R^2 \ge 0 \end{eqnarray}Es importante anotar que las restricciones no holonómicas no se son solamente a aquellas que se expresan en términos de desigualdades. Otro tipo de restricciones no holonómicas comunes son aquellas que se escriben en términos de velocidades. En ese caso, no siempre es posible expresar la condición en la forma:
$$ f_n(\{\vec{r}_i\},t)=0 $$y por lo tanto tampoco podemos llamarla una restricción holonómica.
En las definiciones matemáticas de las restricciones (por ejemplo en la Ec. restriccion_holonomica) aparece el tiempo. ¿Es esto valido?. En el caso del péndulo simple, ciertamente la restricción no depende del tiempo, pero existen otras restricciones que si pueden depender de él. Esto nos lleva a las siguientes definiciones:
El adverbio explícitamente es muy importante aquí, en tanto las restricciones siempre involucran variables dinámicas que cambián intrínsecamente con el tiempo. Una restricción es reónoma solo si el tiempo aparece en su fórmula como variable independiente.
Para ilustrar el caso de una condición reónoma, imagine que en la situación de la Figura (restriccion_no_holonomica) el centro del cuenco se moviera con velocidad constante $u$, de modo que en el tiempo $t$ tuviera abscisa $x_c(t)=ut$. La segunda restricción del sistema se escribiría como:
$$ f_2(\vec r,t)=[x-x_c(t)]^2+y^2-R^2\ge 0 $$o equivalentemente,
$$ f_2(\vec r,t)=(x-ut)^2+y^2-R^2\ge 0 $$Ambas fórmulas corresponden a restricciones reónomas, incluso si en la primera no se escribe la fórmula explícita de $x_c(t)$. De manera más general, entonces, para que una restricción sea reónoma, es necesario que el tiempo aparezca explícitamente o que una cantidad en la restricción dependa del tiempo de una manera conocida e independiente de la solución al problema dinámico.
Nota: el origen de las palabras. La palabra esclerónoma es ciertamente ajena al lenguaje cotidiano. Esta palabra viene del griego antiguo sklero que significa duro y de la partícula nomos o nomía que se refiere a una ley. Es decir, una restricción esclerónoma se llama así porque es una "regla fija", que no se modifica con el tiempo.
La palabra reónomo tampoco es común. Para recordarla basta recordar que reo- viene del griego rheos que significa flujo, corriente. Es decir una restricción reónoma para un griego antiguo sonaría algo así a una regla cambiante.
9.3.1. Fuerzas de restricción¶
Es interesante mencionar en este punto el hecho de que si en un sistema hay una restricción es porque pueden existir interacciones entre las partículas y su entorno que justamente mantengan al sistema constreñido. Así por ejemplo, en el cuerpo que desciende por el cuenco, una fuerza normal $\vec N$ es la que mantiene el bloque a una distancia al menos igual al radio del cuenco.
A este tipo de fuerzas se las conoce como fuerzas de restricción. Estas fuerzas son, en general, muy difíciles de modelar en la mecánica Newtoniana y en la mayoría de las ocasiones es casi imposible conocerlas a priori. La fuerza total sobre una partícula del sistema puede siempre descomponerse como:
$$ \vec{F}_i=\vec{F}^a_i+\vec{f}_i $$donde llamaremos a $\vec{F}^a_i$ la fuerza aplicada (por ejemplo producto de las interacciones entre las partículas) y $\vec{f}_i$ la fuerza de restricción.
Dado que en la aplicación del principio de d'Alambert-Lagrange solo pueden usarse desplazamientos virtuales compatibles con las restricciones, es muy común encontrar que estos desplazamientos terminan siendo perpendiculares a las fuerzas de restricción. Por la misma razón el trabajo virtual realizado por las fuerzas de restricción es nulo.
Este resultado nos permite generalizar reescribir el principio de d'Alambert-Lagrange prescindiendo completamente de las fuerzas de restricción:
\begin{equation} \label{eq:principio_dalambert_aplicadas} \sum_i (\vec{F}_i-\dot{\vec{p}_i})\cdot\delta\vec{r}_i=\sum_i (\vec{F}^a_i-\dot{\vec{p}_i})\cdot\delta\vec{r}_i=0 \end{equation}Esta idea, que parece trivial, en realidad es una de las características más notorias del formalismo Lagrangiano. En este formalismo las desconocidas fuerzas de restricción no juegan (aparte de determinar las restricciones mismas) ningún papel en la dinámica del sistema. Esta es la razón por la cuál, por ejemplo, en el péndulo simple, la tensión, que juega el papel de una fuerza de resticción, no aparece en la ecuación final de movimiento.
9.3.2. Variables generalizadas¶
En el cuadro de Nota de la sección anterior en la que explicabamos el origen de las palabras escléronoma y reónoma bien podríamos haber explicado también la razón por la cuál las restricciones que se expresan con igualdades se conocen como restricciones holónomas. ¿Qué significado tiene el término holónomo en este contexto?.
La palabra holonomía tiene significados muy específicos en matemáticas, en particular en geometría. Si bien la raíz griega holos significa todos, la holonomía hace referencia a la manera como las propiedades geométricas de un sistema se modifican cuando se produce un desplazamiento en el espacio. La holonomía hace referencia por lo tanto en las matemáticas, a una transformación. Esta es la misma acepción por la que se usa la palabra en la mecánica analítica.
Cuando las variables cartesianas de un sistema dinámico están sometidas a restricciones holonómicas, sabemos que es posible describir el estado o configuración del sistema usando un conjunto reducido de variables en lugar de usar todas las coordenadas físicas del sistema. Así por ejemplo, en el caso del péndulo simple, las dos restricciones holonómica impuesta por la cuerda, permiten describir el sistema usando una sola variable, en lugar de las tres coordenadas cartesianas. Esta condición permite introducir un concepto nuevo y crucial en el formalismo Lagrangiano.
Definición 11.18. Número de grados de libertad, M, de un sistema dinámico. El número de grados de libertad de un sistema dinámico es el número mínimo de variables que pueden usarse para describir sin redundancias la configuración del sistema. Si un sistema de $N$ partículas esta sometido a $K$ restricciones holonomas, el número de grados de libertad $M$ es:
$$ M=3N-K $$En el péndulo simple, donde $N=1$ y $K=2$, el número de grados de libertad es $M=3\times1-2=1$, que coincide justamente con nuestra intuición y con el procedimiento que seguimos en la Sección Principio de d'Alambert-Lagrange, donde vimos que solo es necesaria una variable, en particular un ángulo, para especificar la posición de la partícula.
Ahora bien, ¿cuáles son las variables que pueden usarse en lugar de las coordenadas físicas del sistema para describir la configuración del mismo?. La respuesta a esta pregunta no es única. Así por ejemplo, en el caso del péndulo simple podríamos usar la coordenada $x$ solamente, el ángulo $\theta$, la longitud del arco $l$ medido a lo largo del movimiento, la altura $h$ sobre el nivel del techo, etc. Más interesante aún sería uitlizar como variable la velocidad tangencial $v_t$, la energía potencial gravitacional $U$ u otras variables dinámicas. Es decir, para especificar la configuración de un sistema no solo pueden usarse coordenadas sino que también podrían usarse otras cantidades físicas (energías, velocidades, momentos).
Definición 11.19. Variables generalizadas. Cualquier conjunto de $M$ de variables físicas (siendo $M$ el número de grados de libertad) que permitan describir unívocamente la configuración de un sistema dinámico se conocen como variables generalizadas. En lo sucesivo para referirnos a ella usaremos la notación:
$$ \{q_j\}_M $$
Las restricciones holonomas permiten que podamos encontrar funciones matemáticas o transformaciones que conecten las coordenadas del sistema con las variables generalizadas. Estas transformaciones pueden escribirse de forma general como:
\begin{equation} \label{eq:generalizadas_a_coordenadas} \{\vec{x}_{k,i}=\vec{x}_{k,i}(t,\{q_j\}_M)\}_{3N} \end{equation}En términos matemáticos, las coordenadas del sistema y sus variables generalizadas se relacionan a través de una holonomía. Esta es justamente la acepción que tiene esta palabra en el contexto del formalismo lagrangiano.
Aunque no siempre es seguro, asumiremos en lo sucesivo que las funciones en la Ec. (generalizadas_a_coordenadas) pueden ser invertidas para encontrar las variables generalizadas como función de las coordenadas:
\begin{equation} \label{eq:coordenadas_a_generalizadas} \{q_j=q_j(t,\{\vec{r}_i\}_N)\}_M \end{equation}Como ilustración de estas relaciones abstractas, usemos nuevamente el caso del pendulo simple. En este caso si tomamos como variable generalizada $q_1$ el ángulo $\theta$, las ecuaciones de transformación (Ec. generalizadas_a_coordenadas) se escriben como:
$$ \begin{array}{ccc} x_1 (t,q_1) & = & L \sin q_1 \\ y_1 (t,q_1) & = & -L \cos q_1 \\ z_1 (t,q_1) & = & 0 \end{array} $$y su inversa (Ecs. coordenadas_a_generalizadas) como:
$$ q_1 (t,x_1,y_1,z_1) = \tan^{-1}(y_1/x_1) $$Por definición, en el caso en el que un sistema tenga restricciones holónomas esclerónomas, las ecuaciones de transformación no dependerán explícitamente del tiempo. Por otro lado, si las restricciones son holónomas reónomas, el tiempo aparecerá explícitamente en las ecuaciones de transformación.
NOTA: Variables generalizadas independientes. Un importante detalle para tener en cuenta sobre las variables generalizadas es que al elegirlas no se trata simplemente de escoger $M$ números en lugar de $3N$.
Las variables escogidas deben ser tales que sean completamente independientes. Esto significa que una variable puede cambiar sin que otras variables generalizadas cambien también.
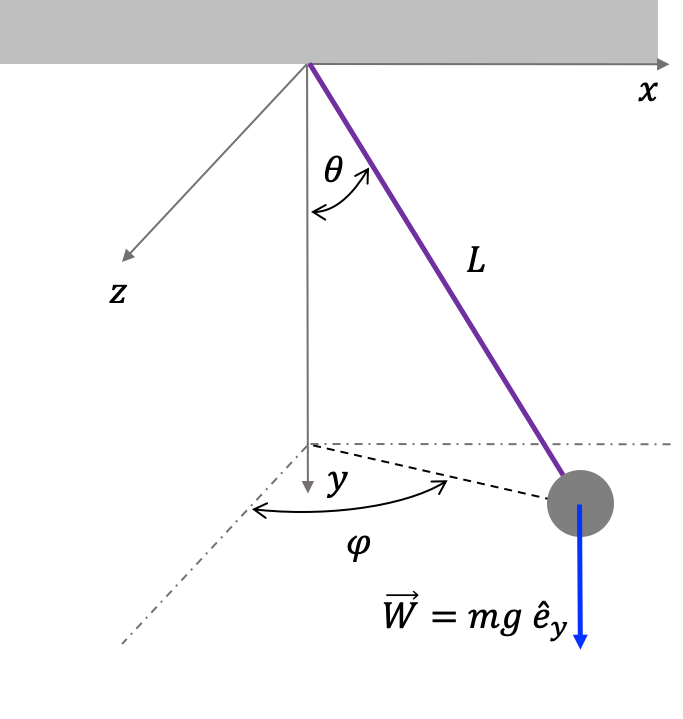
Imaginen por ejemplo el caso del péndulo cónico mostrado en la Figura (pendulo_conico). En esta situación el número de grados de libertad es de 2. ¿cuáles podrían ser las variables generalizadas?.
Podría elegir por ejemplo como variables generalizadas las coordenadas cartesianas $x$, $y$ (tenga presente que $y$ va en la dirección vertical). El problema es que dadas las restricciones del sistema, no es posible variar la coordenada $x$ sin que se produzca un cambio en la coordenada $y$. Es decir, este par de variables no es el más apropiado para describir el sistema. Lo mismo podría ocurrir si elijo la coordenada $y$ y la energía potencial $U$.
Sin embargo si elijo como variables generalizadas la coordenada $z$ y el ángulo $\theta$ es posible imaginar un desplazamiento virtual que implique un cambio en $\theta$ sin que se modifique $z$ y viceversa. O bien, puedo escoger como variables generalizadas (esta sería la elección más apropiada) dos ángulos, el ángulo $\theta$ del péndulo respecto a la vertical, y un ángulo horizontal $\phi$. En este caso, de nuevo, puedo imaginarme desplazamientos virtuales que impliquen el cambio de un ángulo sin que el otro se modifique.
El concepto de variables independientes conduce, finalmente, a la última definición importante de esta sección:
Definición 11.20. Espacio de configuración. Al espacio definido por las variables generalizadas de un sistema dinámico lo llamaremos espacio de configuración. Este espacio es en general diferente del espacio coordenado (con la excepción de sistemas que no tengan restricciones). Cada punto del espacio de configuración esta determinado por $M$ coordenadas (las variables generalizadas del punto).
9.3.3. Propiedades matemáticas de las reglas de transformación¶
Muchos de los resultados sobre los que se basa la construcción del formalismo Lagrangiano dependen de propiedades matemáticas específicas de las reglas de transformación $\vec{r}_i(t,\{q_j\},)$ que definimos antes. He aquí algunas de ellas.
Desplazamientos virtuales en el espacio de configuración. Un desplazamiento virtual en el espacio coordenado se puede expresar como desplazamiento virtual en el espacio de configuraciones usando la regla de la cadena:
$$ \delta\vec{r}_i = \sum_{j=1}^n \left(\frac{\partial \vec{r}_i}{\partial q_j}\delta q_j+\frac{\partial \vec{r}_i}{\partial t}\delta t\right) $$
Dado que por definición, los desplazamientos virtuales no implican un cambio verdadero en la configuración del sistema, los cambios no implican la variable tiempo. De allí que la relación estrictamente correcta es:
\begin{equation} \label{eq:delta_ri_delta_qj} \delta\vec{r}_i = \sum \frac{\partial \vec{r}_i}{\partial q_j}\delta q_j \end{equation}
Velocidad coordenada y velocidad generalizada. Usando también la regla de la cadena podemos escribir las relaciones entre la velocidad en el espacio coordenado y en el espacio de configuración:
\begin{equation} \label{eq:vi_qj} \dot{\vec{r}}_i = \sum \frac{\partial \vec{r}_i}{\partial q_j} \dot{q}_j + \frac{\partial \vec{r}_i}{\partial t} \end{equation}
Arbitrariedad en el orden de las derivadas. Una propiedad útil muy importante de las reglas de transformación es que es posible intercambiar las derivadas temporales con las derivadas espaciales: :
\begin{equation} \label{eq:intercambio_derivadas} \frac{\partial}{\partial q_l}\left(\frac{d \vec{r}_i}{dt}\right) = \frac{d}{dt}\left(\frac{\partial \vec{r}_i}{\partial q_l}\right) \end{equation}
En la sección de Problemas se propone la demostración de esta propiedad.
Regla de cancelación de "puntos". Si derivamos la velocidad son respecto de la componente de la velocidad generalizada $q_k$ obtenemos:
$$ \frac{\partial \dot{\vec{r}}_i}{\partial \dot{q}_k} = \sum \frac{\partial \vec{r}_i}{\partial q_j}\frac{\partial \dot{q}_j}{\partial \dot{q}_k} + \frac{\partial^2 \vec{r}_i}{\partial \dot{q}_j \partial t} $$
Si reconocemos que $\partial\dot{q}_j/\partial\dot{q}_k=\delta_{jk}$ siendo $\delta_{jk}$ el delta de kroenecker, entonces:
\begin{equation} \label{eq:cancelacion_puntos} \frac{\partial \dot{\vec{r}}_i}{\partial \dot{q}_l} = \frac{\partial \vec{r}_i}{\partial q_l} \end{equation}
Llamamos a esta la regla de cancelación de puntos en tanto parece como si los puntos en el numerados y el denominador se cancelaran.
Un ilustración de la regla de cancelación de puntos se puede obtener volviendo sobre el ejemplo del péndulo simple. En ese caso la refla de transformación de la coordenada $x$ se escribe como:
$$ x(q)=L\sin(q) $$Derivando a ambos lados con respecto al tiempo obtenemos:
$$ \dot{x}(q,\dot q)=L\cos(q)\dot{q} $$De donde vemos que efectivamente $\partial\dot x/\partial\dot q$ es igual a $\partial x/\partial q$.
Indice | Previo: FormalismoLagrangiano.Motivacion | Siguiente: FormalismoLagrangiano.EcuacionesLagrange