Indice | Previo: FormalismoLagrangiano.VariablesRestricciones | Siguiente: FormalismoLagrangiano.FuncionLagrangiana
9.4. Las ecuaciones de Lagrange¶
Una vez definidos apropiadamente los concepto en el contexto del formalismo lagrangiano, procederemos en esta sección a encontrar una expresión o una receta matemática que, partiendo del principio de d'Alambert-Lagrange, permita describir un sistema dinámico sin los artificios propios de la aplicación de ese principio.
Para empezar, expresemos el principio de d'Alambert-Lagrange, pero no en términos de las coordenadas cartesianas como lo hicimos en la Ec. (principio_dalambert_aplicadas), sino como función de las variables generalizadas. Para ello, usaremos la expresión que deducimos para los desplazamientos virtuales $\delta \vec{r}_i$ como función de las variables generalizadas y que expresamos como la Ec. (delta_ri_delta_qj). En estos términos el principio se escribe como:
$$ \sum_i \sum_j \vec{F}_i^a \cdot \frac{\partial \vec{r}_i}{\partial q_j} \delta q_j - \sum_i \sum_j \dot{\vec{p}}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j} \delta q_j = 0 $$Consideremos por separado los dos términos de esta ecuación.
El segundo término, que apodaremos temporalmente el termino inercial del principio de d'Alambert-Lagrange, después de algunas transformaciones algebraicas simples, se puede escribir en la forma:
$$ \sum_i \sum_j \dot{\vec{p}}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j} \delta q_j = \sum_j \left \{ \sum_i \frac{d}{dt}\left(m_i\dot{\vec{r}}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j}\right) - m_i\dot{\vec{r}}_i\cdot \frac{d}{dt}\left(\frac{\partial \vec{r}_i}{\partial q_j}\right) \right \} \delta q_j $$Si usamos la ley de cancelación de "puntos" (Ec. cancelacion_puntos) y la arbitrariedad del orden de la derivada parcial y total (Ec. intercambio_derivadas), este término puede escribirse de una forma más conveniente como:
\begin{equation} \label{eq:dalambert_termino_inercial} \sum_i \sum_j \dot{\vec{p}}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j} \delta q_j = \sum_j \left \{ \frac{d}{dt} \left[\frac{\partial}{\partial \dot{q}_j}\sum_i \left(\frac{1}{2} m_i \dot{\vec{r}}_i^2 \right) \right] - \frac{\partial}{\partial q_j} \sum_i \frac{1}{2}m_i \dot{\vec{r}}_i^2 \right \} \delta q_j \end{equation}En esta expresión reconocemos claramente la energía cinética total del sistema$^1$(06.00.00.00.ProblemaNCuerpos.html#problema_ncuerpos) habíamos utilizado la letra $K$ para referirnos a esta cantidad. Aquí, para ser consistentes con buena parte de la literatura en el tema, usaremos en los sucesivo la letra $T$.],
\begin{equation} \label{eq:T} T\equiv\sum_i m_i\dot{\vec{r}_i}^2/2 \end{equation}Es importante entender que en esta expresión, las cantidades $\dot{\vec r}_i$ no son cantidades física convencionales, es decir, los vectores de velocidad de las partículas, como pensaría uno en un primer vistazo. En realidad, por la manera como venimos realizando esta deducción, tanto ${\vec r}_i$ como $\dot{\vec r}_i$ son funciones de las variables generalizadas $\{q_j\}$ y sus derivadas respecto del tiempo $\{\dot q_j\}$. Por esta misma razón, la energía cinética escrita en la forma de la Ec. (T) es en realidad un funcional: una función de funciones.
Otra manera de expresar este hecho fundamental es escribir explícitamente la dependencia intrínseca de la energía cinética de las variables generalizadas:
\begin{equation} \label{eq:T} T(\{q_j\},\{\dot q_j\},t)=\sum_i m_i\dot{\vec{r}_i}(\{q_j\},\{\dot q_j\},t)^2/2 \end{equation}En términos de la energía cinética el término inercial del principio de d'Alambert-Lagrange se puede escribir finalmente como:
\begin{equation} \sum_i \sum_j \dot{\vec{p}}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j} \delta q_j = \sum_j \left \{ \frac{d}{dt} \left[\frac{\partial T}{\partial \dot{q}_j} \right] - \frac{\partial T}{\partial q_j} \right \} \delta q_j \\ \end{equation}Analicemos ahora el término que involucra las fuerzas aplicadas. Por simplicidad en lo sucesivo escribiremos $\vec{F}_i\equiv \vec{F}_i^a$, y por tanto todas las fuerzas a las que nos referimos en lo sucesivo excluyen las fuerzas de restricción. El termino mencionado se puede simplificar si introducimos una cantidad nueva.
\begin{equation} \label{eq:dalambert_termino_fuerza} \sum_j\sum_i \vec{F}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j}\delta q_j = \sum_j Q_j \delta q_j \end{equation}donde a $Q_j$ la llamaremos la fuerza generalizada asociada a la variable $q_j$ y por definición es igual a:
\begin{equation} \label{eq:Q} Q_j \equiv \sum_i \vec{F}_i \cdot \frac{\partial \vec{r}_i}{\partial q_j} \end{equation}Reemplazando el término inercial en la Ec. (dalambert_termino_inercial) con el término de fuerza en la Ec. (dalambert_termino_fuerza), el principio de d'Alambert-Lagrange se puede escribir como:
$$ \sum_j \left[ Q_j - \frac{d}{dt} \left(\frac{\partial T}{\partial \dot{q}_j} \right) + \frac{\partial T}{\partial q_j} \right] \delta q_j = 0 $$En este punto es importante recordar que las variables generalizadas son complemetamente independientes. Recordemos que esto significa que se puede producir un desplazamiento virtual en el que solo una de ellas cambie $\delta q_j\ne 0$, mientras las demás se mantengan constantes. Si aún en esta condición la igualdad anterior es valida podemos concluir que las $M$ cantidades contenidas entre corchetes deben ser simultáneamente cero. Esta conclusión conduce al conjunto de ecuaciones diferenciales que desciben completamente la dinámica del sistema:
\begin{equation} \label{eq:ecuaciones_lagrange} \left\{ \frac{d}{dt} \left(\frac{\partial T}{\partial \dot{q}_j} \right) - \frac{\partial T}{\partial q_j} = Q_j \right\}_M \end{equation}Llamamos a estas las Ecuaciones de Lagrange.
Las ecuaciones de Lagrange, dictan la manera como se relacionan las componentes de la aceleración generalizada $\{\ddot q_j\}$, la velocidad generalizada $\{\dot q_j\}$ y las variables generalizada $\{q_j\}$ con las fuerzas, también generalizadas, que actuan sobre el sistema. Estas ecuaciones son, en el formalismo lagrangiano, el equivalente a las leyes de Newton.
9.4.1. Un ejemplo: el péndulo elástico¶
La deducción realizada en la sección anterior es correcta y general desde el punto de vista matemático. Sin embargo, es tan abstracta que deja muy a menudo, en quién la conoce por primera vez, el sin sabor de que el formalismo Lagrangiano no puede ser una opción mejor que el formalismo newtoniano con sus intuitivos vectores y fuerzas.
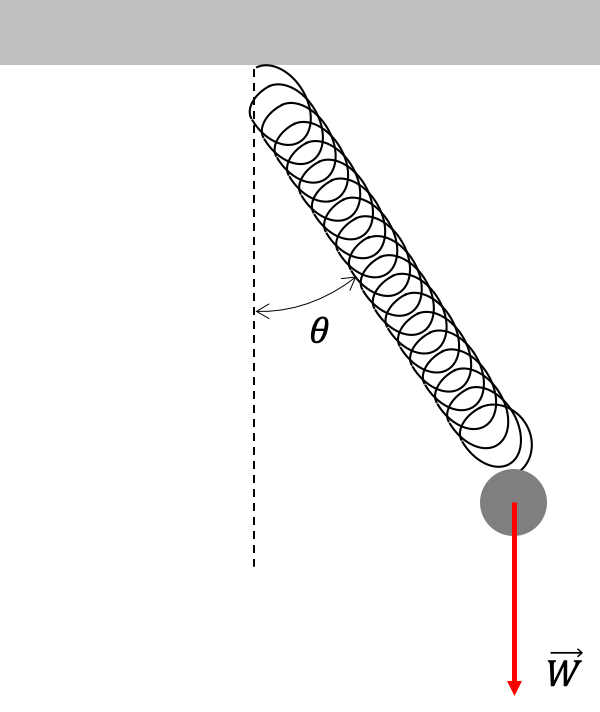
Para hacer más concretos los resultados muy generales y abstractos deducidos aquí y entender mejor las primeras ventajas que exhibe la aproximación lagrangiana a los problemas mecánicos, consideremos un nuevo ejemplo. Hagámoslo esta vez con un sistema mecánico que si bien, no imposible de tratar desde el formalismo vectorial, sí es lo suficientemente complejo para permitirnos, por un lado ilustrar la metodología general del nuevo formalismo y por el otro mostrar sus ventajas evidentes. El sistema, que se ilustra esquemáticamente en la Figura (pendulo_elastico), es el conocido como péndulo elástico.
Para deducir las ecuaciones de Lagrange de este sistema (y de cualquiera que estudiemos) podemos seguir el siguiente conjunto ordenado de pasos:
- Escojer las Variables generalizadas. El péndulo elástico tiene 3 coordenadas cartesianas (1 partícula) y una sola restricción (movimiento en un plano). Esto implica que se necesitan dos variables generalizadas para describir la configuración del sistema. No es difícil identificar como las variables más idóneas para este propósito, el ángulo que forma el péndulo con la vertical $q_1=\theta$ y la elongación del resorte $q_2=e$ (la diferencia entre la longitud instantánea del resorte y su longitud $L$ en equilibrio). Estas dos variables son independientes como se comprueba del hecho de que puedo realizar un desplazamiento virtual en el espacio coordenado, cambiando una de ellas y dejando la otra invariable..
Deducir las reglas de transformación y las velocidades coordenadas. Las reglas de transformación que nos permiten, en este caso, pasar del conjunto de variables generalizadas a las coordenadas cartesianas son:
\begin{equation} \label{eq:pendulo_elastico_transformacion} \begin{array}{rcl} x (q_1,q_2,t)& = & (L+q_2)\sin q_1\\ y (q_1,q_2,t)& = & -(L+q_2)\cos q_1\\ z (q_1,q_2,t)& = & 0 \end{array} \end{equation}
Como vemos la restricciones y por lo tanto las reglas de transformación, son esclerónomas (no dependen explícitamente del tiempo).
Una de las funciones básicas de las reglas de transformación es escribir las velocidades coordenadas como función de las variables generalizadas y sus velocidades. Derivando las expresiones anteriores, obtenemos:
$$ \begin{aligned} \dot x (q_1,q_2,\dot q_1,\dot q_2,t)& = & (L+q_2)\cos q_1\dot q_1+\dot q_2\sin q_1\\ \dot y (q_1,q_2,\dot q_1,\dot q_2,t)& = & (L+q_2)\sin q_1\dot q_1-\dot q_2\cos q_1\\ \end{aligned} $$
Escribir la función de energía cinética y calcular sus derivadas parciales. Usando las reglas de transformación podemos ahora escribir la función de energía cinética. Con un poco de álgebra el resultado es:
$$ T((q_1,q_2,\dot q_1,\dot q_2,t)=\frac{1}{2}m\left[(1+q_2)^2\dot q_1^2 +\dot q_2^2\right] $$
Con esta forma de la función podemos ahora obtener las derivadas parciales de $T$ que necesitaremos más adelante:
\begin{eqnarray} \nonumber \frac{\partial T}{\partial q_1} & = & 0\\ \nonumber \frac{\partial T}{\partial q_2} & = & m(L+q_2)\dot q_1^2\\ \nonumber \frac{\partial T}{\partial \dot q_1} & = & m(L+q_2)^2\dot q_1\\ \nonumber \frac{\partial T}{\partial \dot q_2} & = & m\dot q_2\\ \end{eqnarray} y las derivadas totales respecto al tiempo de los dos últimos términos:
\begin{eqnarray} \nonumber \frac{d}{dt}\frac{\partial T}{\partial \dot q_1} & = & 2 m(L+q_2)\dot q_2\dot q_1+m(L+q_2)^2\ddot q_1\\ \nonumber \frac{d}{dt}\frac{\partial T}{\partial \dot q_2} & = & m\ddot q_2\\ \end{eqnarray}
Calcular la forma de las fuerzas generalizadas. Necesitamos escribir las fuerzas generalizadas asociadas a cada una de las variables generalizadas en el problema. Para ello es necesario conocer, primero, la expresión de las fuerzas coordenadas como función de las variables generalizadas. Es fácil mostrar que las componentes cartesianas de las fuerzas que actúan sobre el péndulo son simplemente:
$$ \vec F=-kq_2\sin q_1\hat{e}_x+(-W+kq_2\cos q_1)\hat{e}_y $$
De allí la fuerza generalizada asociada con la primera variable ($q_1\equiv\theta$) es:
$$ Q_1 = \sum_i \vec F_i\cdot\frac{\partial \vec r_j}{\partial q_1} =\vec F\cdot\frac{\partial \vec r}{\partial q_1}=\vec F\cdot\left(\frac{\partial x}{\partial q_1}\hat{e}_x+\frac{\partial y}{\partial q_1}\hat{e}_y\right) $$
Que, con un poco de algebra, puede probarse es igual a:
$$ Q_1 = -W(L+q_2)\sin q_1 $$
De la misma manera puede calcularse la fuerza generalizada asociada con la segunda variable generalizada para obtener:
$$ Q_2 = W\cos q_1 - k q_2 $$
Escribir explícitamente las ecuaciones de Lagrange. Ahora podemos reemplazar algunos de los insumos matemáticos obtenidos en los apartes anteriores en las ecuaciones de Lagrange (Ecs. ecuaciones_lagrange):
$$ 2 m(L+q_2)\dot q_2\dot q_1+m(L+q_2)^2\ddot q_1 = -W(L+q_2)\sin q_1 $$
$$ m\ddot q_2-m(L+q_2)\dot q_1^2=W\cos q_1 - k q_2 $$
Como vemos, en su forma explícita, las ecuaciones de Lagrange son ecuaciones diferenciales de segundo orden en las variables generalizadas.
Escribir explícitamente las ecuaciones de movimiento. Normalmente las ecuaciones de Lagrange se obtienen de forma desordenada con términos que admiten todavía alguna simplificación. Particularmente interesante es explorar la posibilidad de organizar las ecuaciones dejando los términos de segundas derivadas en un sólo lado de la ecuación (lo que facilita su implementación y solución numérica, cuando haya lugar a esta aproximación). En este caso, las ecuaciones de Lagrange obtenidas en el numeral anterior se pueden escribir como:
\begin{eqnarray} \label{eq:pendulo_elastico_ec_q1} \ddot q_1 & = & -\frac{2\dot q_1\dot q_2}{L+q_2}-\frac{g\sin q_1}{L+q_2}\\ \label{eq:pendulo_elastico_ec_q2} \ddot q_2 & = & g\cos q_1 - (k/m)q_2+(L+q_2)\dot q_1^2 \end{eqnarray}
El procedimiento realizado aquí no requiere de ningún "truco", exige una mínima intuición física y solo necesita paciencia y un buen manejo del cálculo diferencial y el álgebra. El resultado final, las ecuaciones de movimiento, si bien puede obtenerse usando la mecánica newtoniana, es inevitable si se siguen cuidadosamente los pasos descritos. He aquí la primera ventaja del formalismo Lagrangiano: su poderosa, por llamarlo de alguna manera, inevitabiliad analítica.
Como acostumbramos hacer en el libro, pongamos a prueba el resultado obtenido resolviendo la ecuación de movimiento y visualizando la dinámica del sistema. Para ello, primero debemos linealizar las ecuaciones de movimiento (Esc. pendulo_elastico_ec_q1 y pendulo_elastico_ec_q2) e implementarlas como una rutina:
def edm_penduloelastico(Y,t,L,k,m):
#Constantes físicas
g=9.81
# Lee variables
q1,q2,q1p,q2p=Y
# Velocidades
dq1dt=q1p
dq2dt=q2p
# Aceleraciones
from numpy import sin,cos
dq1pdt=(-g*sin(q1)-2*q1p*q2p)/(L+q2)
dq2pdt=(L+q2)*q1p**2+g*cos(q1)-(k/m)*q2
return [dq1dt,dq2dt,dq1pdt,dq2pdt]
Definir las propiedades del sistema y sus condiciones iniciales. Para ello debemos recordar el significado físico de $q_1$ (un ángulo) y de $q_2$ (elongación del resorte). Para este ejemplo soltaremos el péndulo en reposo en un ángulo de $30^\circ$ y con una elongación inicial de $0.1$.
#Propiedades del sistema
L=1.0
k=20.0
m=1.0
#Condiciones iniciales
from numpy import pi
y=[pi/3,0.1,0.0,0.0]
#Tiempos de integración
from numpy import linspace
Nt=200
ts=linspace(0,10,Nt)
Finalmente resolvemos numéricamente las ecuaciones de movimiento y extraemos el valor de las cariables generalizadas como función del tiempo:
from scipy.integrate import odeint
solucion=odeint(edm_penduloelastico,y,ts,args=(L,k,m))
q1s=solucion[:,0]
q2s=solucion[:,1]
Podemos visualizar el valor de las variables generalizadas como función del tiempo con el siguiente algortimo:
%matplotlib inline
import matplotlib.pyplot as plt
fig,axs=plt.subplots(2,1,sharex=True)
axs[0].plot(ts,q1s*180/pi)
axs[0].set_ylabel("Ángulo")
axs[1].plot(ts,q2s)
axs[1].set_ylabel("Elongación")
axs[1].set_xlabel("Tiempo")
fig.tight_layout()
Sin embargo, la mejor manera de comprobar que la dinámica se ajusta a nuestras expectativas es mostrar el movimiento del sistema en el espacio de coordenadas. Para ello es necesario que hagamos la transformación de variables generalizadas a coordenadas usando las reglas en las Ecs. (pendulo_elastico_transformacion)
from numpy import sin,cos,zeros_like
xs=(L+q2s)*sin(q1s)
ys=-(L+q2s)*cos(q1s)
zs=zeros_like(xs)
Una gráfica de la trayectoria de la partícula en el espacio físico se obtiene finalmente con este código:
fig=plt.figure()
ax=fig.gca()
ax.plot(xs,ys)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Espacio Coordenado")
from pymcel.plot import fija_ejes_proporcionales
fija_ejes_proporcionales(ax,(xs,ys),xcm=0);
Que finalmente coincide con lo que esperabamos: la partícula oscila como péndulo, pero su distancia al punto de pivote del resorte cambia también.
--end:hide_pdf--
Indice | Previo: FormalismoLagrangiano.VariablesRestricciones | Siguiente: FormalismoLagrangiano.FuncionLagrangiana