10.7. Transformaciones canónicas¶
Una de las características más poderosas del formalismo Hamiltoniano es la manera como puede manipularse tanto el espacio de fase, como la función hamiltoniana misma, para simplificar la solución a problemas dinámicos muy complicados o para analizar algunas de sus propiedades más sutiles.
Para ilustrar esta flexibilidad del formalismo consideremos por ejemplo un problema muy estudiado en los últimos dos capítulos: el oscilador armónico simple. Una cuerpo de masa $m$ esta unido a un resorte de constante elástica $k$ y solo puede oscilar en una dimensión. Es fácil mostrar que el Hamiltoniano del sistema es simplemente:
$$ H_\mathrm{MAS}(x,p_x)=\frac{p_x^2}{2m}+\frac{1}{2}kx^2=\frac{1}{2m}(p_x^2+m^2\omega^2 x^2) $$donde $\omega\equiv\sqrt{k/m}$.
Consideremos ahora el siguiente cambio de coordenadas:
\begin{eqnarray} \nonumber p_x & = & C\sqrt{P}\cos X\\ \nonumber x & = & \frac{C\sqrt{P}}{m\omega} \sin X \end{eqnarray}donde $C$ es una constante desconocida.
Reemplazando en el Hamiltoniano obtenemos una nueva función:
$$ K(X,P)\equiv H(x(X,P),p_x(X,P))=\frac{C^2P}{2m} $$Aunque esta función es mucho más simple que el Hamiltoniano original no podemos asegurar que $K$ sea una alternativa válida al Hamiltoniano para describir la dinámica del sistema. La razón esencial de esto es que no sabemos si las nuevas variables $X$ y $P$, junto con la nueva función $K$ satisfacen un conjunto de ecuaciones idéntica a las ecuaciones canónicas:
\begin{eqnarray} \label{eq:dQ_K} \dot X = +\frac{\partial K}{\partial P}\\ \label{eq:dP_H} \dot P = -\frac{\partial K}{\partial X}\\ \end{eqnarray}Definición 11.26. Transformación Canónica. Una transformación puntual (invertible) en el espacio de fase:
\begin{eqnarray} \label{eq:Q_transformacion} Q_k & = & Q_k(\{q_j\},\{p_j\},t)\\ \label{eq:P_transformacion} P_k & = & P_k(\{q_j\},\{p_j\},t) \end{eqnarray}se llama transformación canónica si es posible encontrar una función $K(\{Q_k\},\{P_k\},t)$ tal que:
\begin{eqnarray} \nonumber \left\{\dot Q_j = +\frac{\partial K}{\partial P_j}\right\}_M\\ \nonumber \left\{\dot P_j = -\frac{\partial K}{\partial Q_j}\right\}_M\\ \end{eqnarray}En otras palabras una transformación es canónica si la variable correspondiente al momento sigue siendo canónica conjugada de la variable generalizada correspondiente.
¿Cómo saber exactamente si una transformación es canónica? ¿qué condiciones matemáticas deben cumplir las ecuaciones de transformación (Q_transformacion) y (P_transformacion) o sus inversas para satisfacer que exista una función que relacione sus tasas de variación a través de ecuaciones canónicas?.
El conjunto de transformaciones consideradas en la definición anterior es muy amplio e incluye transformaciones en las que es posible que la relación entre el nuevo conjunto de variables y el conjunto original dependa del tiempo. Si nos restringimos a transformaciones puntuales que no dependen del tiempo (como la transformación postulada en el ejemplo del oscilador armónico simple):
\begin{eqnarray} \label{eq:Q_transformacion_restringidas} Q_k & = & Q_k(\{q_j\},\{p_j\})\\ \label{eq:P_transformacion_restringidas} P_k & = & P_k(\{q_j\},\{p_j\}) \end{eqnarray}la condición de transformación canónica adopta una forma relativamente simple.
Una transformación geométrica como la indicada arriba no debería cambiar el Hamiltoniano mismo. A lo sumo podemos postular que la función $K$ de la definición no es otra cosa el Hamiltoniano original en el que simplemente cambiamos las variables originales por las nuevas variables a través de las transformaciones inversas :
$$ K(\{Q_j\},\{P_j\},t)= H(\{q_j(\{Q_k,P_k\})\},\{p_j(\{Q_k,P_k\})\},t) $$La pregunta que nos hacemos es si esta nueva función $K$ es tal que:
\begin{equation} \label{eq:dotQ_K} \dot{Q}_j=\frac{\partial K}{\partial P_j} \end{equation}En la igualdad anterior, $Q_j$ y $P_j$ son consideradas variables independientes. Pero podemos, por un momento tratarlas como las funciones de transformación, que a su vez dependen de $q_j$ y $p_j$. En este caso:
\begin{equation} \label{eq:dotQ_simplectica} \dot{Q}_j=\frac{\partial Q_j}{\partial q_j}\dot{q}_j+\frac{\partial Q_j}{\partial p_j}\dot{p}_j =\frac{\partial H}{\partial p_j}\left(\frac{\partial Q_j}{\partial q_j}\right)_{q,p}-\frac{\partial H}{\partial q_j}\left(\frac{\partial Q_j}{\partial p_j}\right)_{q,p} \end{equation}donde hemos utilizado las ecuaciones canónicas para reemplazar $\dot{q}_j$ y $\dot{p}_j$ en el lado derecho.
La notación $(\partial Q_j/\partial p_j)_{q,p}$ y $(\partial Q_j/\partial q_j)_{q,p}$ refuerza el hecho de que en estas derivadas las variables originales $q$ y $p$ juegan el papel de variables independientes.
Por otro lado, por la regla de la cadena y teniendo en cuenta las transformaciones inversas: \begin{equation} \label{eq:dotK_simplectica} \frac{\partial K}{\partial P_j}=\frac{\partial K}{\partial p_j}\frac{\partial p_j}{\partial P_j}+\frac{\partial K}{\partial q_j}\frac{\partial q_j}{\partial P_j}= \frac{\partial H}{\partial p_j}\left(\frac{\partial p_j}{\partial P_j}\right)_{Q,P}+\frac{\partial H}{\partial q_j}\left(\frac{\partial q_j}{\partial P_j}\right)_{Q,P} \end{equation} aquí se ha usado el hecho de que en realidad $K$ es el mismo Hamiltoniano $H$ pero expresado en términos de las nuveas variables; pero cuando se toma una derivada como $\partial K/\partial q_j$ en realidad necesaitamos volver a la forma funcional original de $H$ y es por eso que hacemo $\partial K/\partial q_j=\partial H/\partial q_j$.
Para que se cumpla entonces la Ec. (dotQ_K), el lado derecho de las Ecs. (dotQ_simplectica) y (dotK_simplectica) deben ser iguales. Comparando término a término, la igualdad se satisface si y solo si:
\begin{eqnarray} \label{eq:dQdq_simplectica} \left(\frac{\partial Q_j}{\partial q_j}\right)_{q,p} & = & \left(\frac{\partial p_j}{\partial P_j}\right)_{Q,P}\\ \label{eq:dQdp_simplectica} \left(\frac{\partial Q_j}{\partial p_j}\right)_{q,p} & = & \left(\frac{\partial q_j}{\partial P_j}\right)_{Q,P} \end{eqnarray}Si se utilizá un procedimiento análogo pero partiendo de la ecuación:
$$ \dot{P}_j=-\frac{\partial K}{\partial Q_j} $$se obtienen las condiciones:
\begin{eqnarray} \label{eq:dPdq_simplectica} \left(\frac{\partial P_j}{\partial q_j}\right)_{q,p} & = & -\left(\frac{\partial p_j}{\partial Q_j}\right)_{Q,P}\\ \label{eq:dPdp_simplectica} \left(\frac{\partial P_j}{\partial p_j}\right)_{q,p} & = & \left(\frac{\partial q_j}{\partial Q_j}\right)_{Q,P} \end{eqnarray}A las condiciones expresadas en las Ecs. (dQdq_simplectica)-(dPdp_simplectica) se las conoce como condiciones directas para transformaciones canónicas restringidas.
Podemos usar este conjunto de condiciones para poner a prueba las transformaciones propuestas antes para el movimiento armónico simple:
\begin{eqnarray} \nonumber p_x & = & C\sqrt{P}\cos X\\ \nonumber x & = & \frac{C\sqrt{P}}{m\omega} \sin X \end{eqnarray}Para ello necesitamos primero obtener las transformaciones inversas:
\begin{eqnarray} \nonumber P & = & \frac{1}{C^2}(p_x^2+m^2\omega^2 x^2)\\ \nonumber X & = & \tan^{-1}\left(\frac{m\omega x}{p_x}\right) \end{eqnarray}Pongamos a prueba la transformación con la condición:
$$ \left(\frac{\partial Q_j}{\partial q_j}\right)_{q,p} = \left(\frac{\partial p_j}{\partial P_j}\right)_{Q,P} $$que en este caso se expresaría como:
$$ \left(\frac{\partial X}{\partial x}\right)_{x,p_x} = \left(\frac{\partial p_x}{\partial P}\right)_{X,P} $$El lado izquierdo de esta ecuación se puede escribir como:
$$ \left(\frac{\partial X}{\partial x}\right)_{x,p_x}=\frac{m\omega p_x}{p_x^2+m^2\omega^2 x^2} $$Si usamos las reglas de transformación para $p_x$ y para $P$ la anterior relación queda:
\begin{equation} \label{eq:dXdx} \left(\frac{\partial X}{\partial x}\right)_{x,p_x} =\frac{m\omega C\sqrt{P}\cos X}{C^2 P} =\frac{m\omega\cos X}{C\sqrt{P}} \end{equation}Por otro lado:
\begin{equation} \label{eq:dpdP} \left(\frac{\partial p_x}{\partial P}\right)_{X,P}=\frac{C\cos X}{2\sqrt{P}} \end{equation}Es decir, la transformación:
\begin{eqnarray} \nonumber x & = & \sqrt{\frac{2 P}{m\omega}} \sin X\\ \nonumber p_x & = & \sqrt{2m\omega P}\cos X \end{eqnarray}satisface al menos una de las condiciones directas para ser una transformación canónica. Es posible mostrar (ver Problemas al final del capítulo) que esta transformación cumple también todas las demás condiciones directas, de donde concluimos que es canónica y que el hamiltoniano del sistema es, en el nuevo sistema de coordenadas:
\begin{equation} \label{eq:MAS_hamiltoniano_transformado} K=\omega P \end{equation}¿Qué importancia tienen las transformaciones canónicas?. El ejemplo del oscilador armónico simple (si bien muy sencillo para una técnica tan sofisticada) nos permite ilustrar nuevamente el poder de este tipo de transformaciones. Dicho Hamiltoniano en el nuevo sistema de coordenadas dado por la Ec. (MAS_hamiltoniano_transformado), tiene una serie de propiedades muy interesantes:
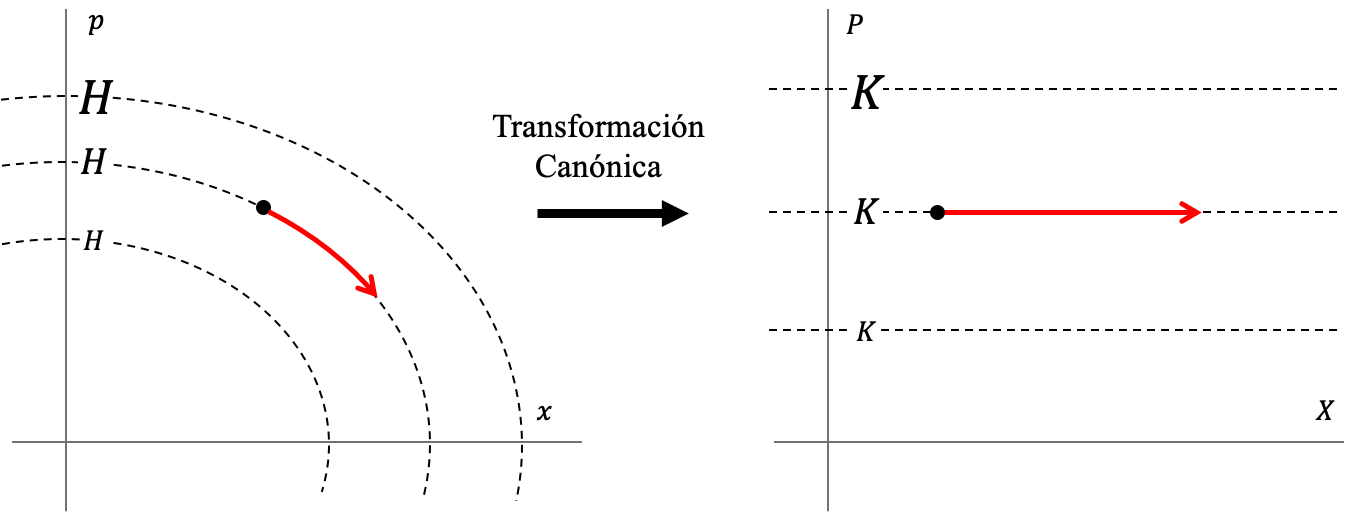
A diferencia del Hamiltoniano original, en el nuevo sistema de variables, $X$ es cíclica y por lo tanto su momento canónico conjugado $P$ es constante. Esto básicamente significa que la transformación canónica realizada convirtió el espacio de fase, de uno en el que los contornos de igual valor de $H$ eran elipses, a otro en el que son líneas rectas horizontales (ver Figura (transformacion_canonica)). La dinámica en el espacio transformado es trivial. Dado un punto inicial, el sistema se mueve sobre una línea recta horizontal con ecuación de movimiento dado por:
$$ \dot X=\frac{\partial K}{\partial P}=\omega $$ que puede resolverse analíticamente como:
$$ X=X_0+\omega t $$
Tanto el Hamiltoniano original, como el nuevo, satisfacen las condiciones que permiten identificarlo, primero como una constante y segundo como la energía mecánica:
$$ \omega P=E $$ de donde se sigue que:
$$ P=\frac{E}{\omega} $$ que habíamos dicho también es constante.
- Las propiedades del sistema en el nuevo conjunto de variables y los resultados muy sencillos obtenidos en los apartes anteriores, nos permiten finalmente escribir la solución analítica al problema en las coordenadas generalizadas originales como:
Es decir, en este caso, la transformación canónica propuesta nos permitió resolver completamente el problema al simplificar significativamente la dinámica del sistema en el espacio de fase. Esta es una de las aplicaciones posibles de este tipo de transformaciones.