Indice | Previo: FormalismoHamiltoniano.EspacioFase | Siguiente: FormalismoHamiltoniano.TransformacionesCanonicas
10.6. Simetrías y candidates conservadas¶
Uno de las ventajas más notables del formalismo Lagrangiano frente al formalismo vectorial de la mecánica, era la posibilidad de conocer propiedades de un sistema dinámico sin resolver explícitamente las ecuaciones de movimiento, estudiando únicamente las simetrías del Lagrangiano. Con estas simetrías era posible, a través del teorema de Noether para el Lagrangiano, deducir las cuadraturas o cantidades conservadas.
Siendo el Hamiltoniano un formalismo escalar con una conexión profunda con el formalismo Lagrangiano, es válido hacerse la pregunta de cómo esos resultados, simetrías y cantidades conservadas, se aplican aquí. En los siguientes párrafos nos ocuparemos de estudiar la relación entre las simetrías del Hamiltoniano y las constantes de movimiento asociadas con ellas.
10.6.1. Variables cíclicas¶
Como sucede en el formalismo Lagrangiano, las variables cíclicas del Hamiltoniano (variables que no aparecen explícitamente en su fórmula) corresponden directamente a cantidades conservadas. En el nuevo formalismo, sin embargo, estas cantidades conservadas son triviales.
Si analizamos directamente las ecuaciones canónicas de Hamilton:
\begin{eqnarray} \nonumber \left\{\dot q_j = +\frac{\partial H}{\partial p_j}\right\}_M\\ \nonumber \left\{\dot p_j = -\frac{\partial H}{\partial q_j}\right\}_M\\ \end{eqnarray}vemos que basta que una de las variables del Hamiltoniano no aparezca explícitamente en su fórmula, para que la variable conjugada correspondiente sea inmediatamente una constante de movimiento.
Proposición: Variables cíclicas del Hamiltoniano. Si una variable del Hamiltoniano $q_k$ o $p_k$, no aparece explícitamente en su fórmula, entonces la variable canónica conjugada $p_k$ o $q_k$ es una constante de movimiento. Simbólicamente:
$$ \mathrm{Si}\;\frac{\partial H}{\partial q_k}=0\;\rightarrow\;p_k:{\rm cte} $$o bien:
$$ \mathrm{Si}\;\frac{\partial H}{\partial p_k}=0\;\rightarrow\;q_k:{\rm cte} $$
Nótese el contraste entre las cantidades conservadas asociadas a las variables cíclicas del Hamiltoniano y aquellas del lagrangiano. De un lado, mientras en este último formalismo, solo las variables generalizadas cíclicas tenían asociada una cantidad conservada, sus velocidades generalizadas $\dot q_j$ no. Además la fórmula de la cantidad conservada asociada a una variable cíclica $q_k$:
$$ p_k=\frac{\partial L}{\partial q_k} $$podía llegar a ser realmente complicada.
Más interesantes aún son las implicaciones geométricas de esta simetría del Hamiltoniano (recordemos que este formalismo tiene una profunda raíz geométrica). Un ejemplo simple puede ayudarnos a entender mejor esas implicaciones.
10.6.2. Un ejemplo: el péndulo cónico¶
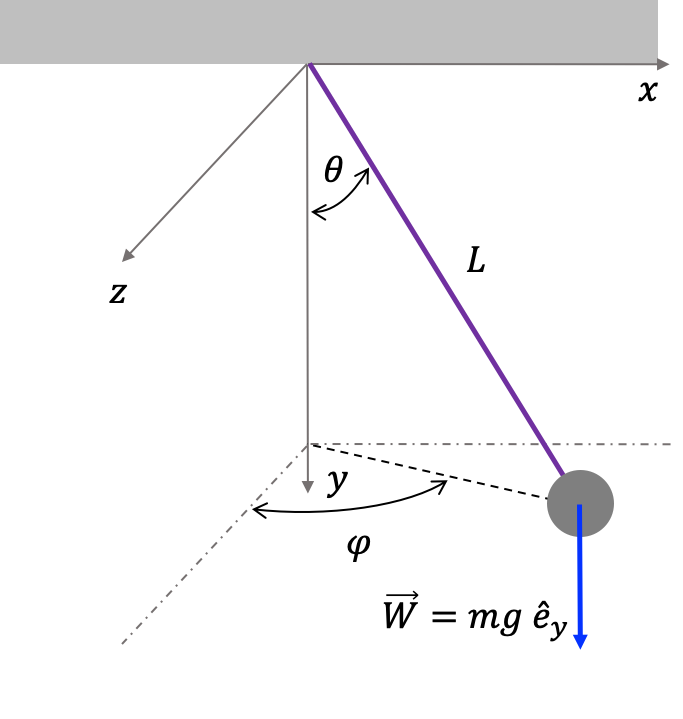
Volvamos nuestra atención sobre un sistema que habíamos introducido ya en la Sección Variables generalizadas. En la Figura (hamiltoniano_pendulo_conico) reproducimos una representación esquemática del sistema que se conoce como el péndulo cónico.
Como vemos el problema tiene dos grados de libertad y por lo tanto puede ser descrito por dos variables generalizadas independientes $\theta$ y $\phi$. Sin embargo el espacio de fase del problema es (para los estándares de los ejemplos simples considerados hasta ahora) enorme. Teine en total de 4 dimensiones ($\theta$, $\phi$, $p_\theta$, $p_\phi$). Este hecho hace que sea muy difícil representar gráficamente o siquiera imaginarse la dinámica del sistema en el espacio de fase. Las simetrías del problema pueden sin embargo ayudarnos en la representación geométrica de la dinámica.
Para escribir el Hamiltoniano del péndulo cónico, debemos primero escribir el Lagrangiano. No es difícil mostrar que dicho Lagrangiano tiene la forma (ver Problemas al final del capítulo):
$$ L_\mathrm{PC}=\frac{1}{2}m(L^2\dot\theta^2+L^2\sin^2\theta\dot\phi)+mgL\cos\theta $$Los momentos canónicos conjugados serán en este caso:
$$ \begin{array}{rclcl} p_\theta & = & \partial L/\partial \theta & = & mL^2\dot\theta\\ p_\phi & = & \partial L/\partial \phi & = & mL^2\sin^2\theta\dot\phi \end{array} $$Con esto el Lagrangiano escrito en términos de $p_\theta, p_\phi$ será:
$$ L_{{\rm PC},qp}=\frac{p_\theta^2}{2mL^2}+\frac{p_\phi^2}{2mL^2\sin^2\theta}+mgL\cos\theta $$Y el Hamiltoniano
$$H_\mathrm{PC}=p_\theta\dot\theta+p_\phi\dot\phi-L_{{\rm PC},qp}$$queda:
$$ H_\mathrm{PC}=\frac{p_\theta^2}{2mL^2}+\frac{p_\phi^2}{2mL^2\sin^2\theta}-mgL\cos\theta $$Como vemos en la fórmula anterior, la variable $\phi$ es cíclica, por lo tanto su momento canónico conjugado es una constante de movimiento:
$$p_\phi\equiv\alpha_\phi={\rm cte.}$$Con esta constante, las ecuaciones de movimiento para las variables restantes será:
\begin{eqnarray} \label{eq:edm_pendulo_conico} \dot\phi & = & \frac{\alpha_\phi^2}{mL^2\sin^2\theta}\\ \nonumber \dot\theta & = & \frac{p_\theta^2}{mb^2}\\ \nonumber \dot p_\theta & = & \frac{\alpha^2_\phi\cos\theta}{mb^2\sin^3\theta}-mbg\sin\theta \end{eqnarray}y el Hamiltoniano del sistema se escribe como:
$$ H=\frac{p_\theta^2}{2mb^2}+\frac{\alpha_\phi^2}{2mb^2\sin^2\theta}-mgb\cos\theta $$Vemos pues que con la identificación de una variable cíclica, este sistema que tiene dos grados de libertad (y por lo tanto un espacio de fase de 4 dimensiones) se puede describir completamente en un espacio de solo 3 dimensiones : $\theta$, $\phi$ y $p_\theta$. En otras palabras, el espacio de fase sigue siendo de 4 dimensiones pero la dinámica ocurre exlusivamente sobre la hipersuperficie constante $p_\phi=\alpha_\phi$.
Para visualizar el movimiento del sistema en el espacio de coordenadas y el espacio fase, implementemos primeros las ecuaciones de movimiento (Ecs. edm_pendulo_conico):
def edm_penduloconico_hamiltoniano(Y,t,alfa_fi,L,m):
#Constantes
g=9.81
#Variables
teta=Y[0]
fi=Y[1]
pteta=Y[2]
#Derivadas
from numpy import sin,cos
dtetadt=pteta/(m*L**2)
dfidt=alfa_fi/(m*L**2*sin(teta)**2)
dptetadt=alfa_fi**2*cos(teta)/(m*L**2*sin(teta)**3)-m*L*g*sin(teta)
return [dtetadt,dfidt,dptetadt]
Las propiedades del sistema, condiciones y solución numérica de las ecuaciones de movimiento se obtienen con el siguiente algoritmo:
#Propiedades
g=9.81
L=1.0
m=1.0
#Factores de conversión
from numpy import pi,linspace
grados=pi/180
#Condiciones iniciales
teta_0=15*grados
fi_0=0.0*grados
pteta_0=0.0
alfa_fi=0.8
#Tiempos de integración
from numpy import pi,sqrt,linspace
T=2*pi*sqrt(L/g)
Nt=300
ts=linspace(0,3*T,Nt)
#Solución numérica
from scipy.integrate import odeint
solucion=odeint(edm_penduloconico_hamiltoniano,
[teta_0,fi_0,pteta_0],ts,
args=(alfa_fi,L,m))
#Extrae momentos
tetas=solucion[:,0]
fis=solucion[:,1]
ptetas=solucion[:,2]
#Coordenadas cartesianas
from numpy import sin,cos
xs=L*sin(tetas)*cos(fis)
ys=L*sin(tetas)*sin(fis)
zs=-L*cos(tetas)
Un gráfico de la trayectoria de la partícula en el espacio coordenado (físico) y en el espacio de fase, se puede obtener con el siguiente algoritmo:
%matplotlib inline
#Preparación del gráfico
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(8,4))
ax_coord=fig.add_subplot(121,projection='3d')
ax_fase=fig.add_subplot(122,projection='3d')
#Gráfico en el espacio de coordenadas
ax_coord.plot(xs,ys,zs,'k-')
#Gráfico en el espacio de fases
ax_fase.plot(tetas,fis,ptetas,'b-')
#Decoración
ax_coord.set_xlabel("$x$")
ax_coord.set_ylabel("$y$")
ax_coord.set_zlabel("$z$")
ax_coord.set_title("Espacio coordenado")
from pymcel.plot import fija_ejes3d_proporcionales
fija_ejes3d_proporcionales(ax_coord)
ax_fase.set_xlabel("$\\theta$")
ax_fase.set_ylabel("$\phi$")
ax_fase.set_zlabel("$p_\\theta$")
ax_fase.set_title("Espacio de fase")
fig.tight_layout()
El siguiente algoritmo condensa los algoritmos vistos en esta sección y produce una versión animada del movimiento del péndulo, tanto en el espacio coordenado como en el espacio de fase:
%%capture
#Propiedades
g=9.81
L=1.0
m=1.0
#Condiciones iniciales
teta_0=15*grados
fi_0=0.0*grados
pteta_0=0.0
alfa_fi=0.8
#Tiempos de integración
T=2*pi*sqrt(L/g)
Nt=200
ts=linspace(0,3*T,Nt)
#Solución numérica
from scipy.integrate import odeint
solucion=odeint(edm_penduloconico_hamiltoniano,
[teta_0,fi_0,pteta_0],ts,
args=(alfa_fi,L,m))
tetas=solucion[:,0]
fis=solucion[:,1]
ptetas=solucion[:,2]
#Coordenadas cartesianas
xs=L*sin(tetas)*cos(fis)
ys=L*sin(tetas)*sin(fis)
zs=-L*cos(tetas)
#Preparación del gráfico
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(8,4))
ax_coord=fig.add_subplot(121,projection='3d')
ax_fase=fig.add_subplot(122,projection='3d')
#Gráfico en el espacio de coordenadas
ax_coord.plot(xs,ys,zs,'k-',alpha=0.3)
punto_coord,=ax_coord.plot([],[],[],'ko',ms=5)
cuerda,=ax_coord.plot([],[],[],'k-')
#Gráfico en el espacio de fases
ax_fase.plot(tetas,fis,ptetas,'b-',alpha=0.3)
punto_fase,=ax_fase.plot([],[],[],'bo',ms=5)
#Decoración
ax_coord.set_xlabel("$x$")
ax_coord.set_ylabel("$y$")
ax_coord.set_zlabel("$z$")
ax_coord.set_title("Espacio coordenado")
from pymcel.plot import fija_ejes3d_proporcionales
fija_ejes3d_proporcionales(ax_coord)
ax_fase.set_xlabel("$\\theta$")
ax_fase.set_ylabel("$\phi$")
ax_fase.set_zlabel("$p_\\theta$")
ax_fase.set_title("Espacio de fase")
fig.tight_layout()
def animacion(it):
punto_coord.set_data_3d([xs[it]],[ys[it]],[zs[it]])
cuerda.set_data_3d([0,xs[it]],[0,ys[it]],[0,zs[it]])
punto_fase.set_data_3d([tetas[it]],[fis[it]],[ptetas[it]])
return punto_coord,cuerda,punto_fase
from matplotlib import animation
anim=animation.FuncAnimation(fig,animacion,frames=Nt,interval=50,blit=True,repeat=False);
Para tener más control sobre la animación se puede usar este algoritmo:
from matplotlib import rcParams
rcParams['animation.embed_limit']=2**128
from IPython.display import HTML
HTML(anim.to_jshtml())