Indice | Previo: Problema2Cuerpos.AproximacionJerarquico | Siguiente: Problema2Cuerpos.SPICE

7.14. Introducción a la teoría de perturbaciones

En la Sección Energía específica relativa vimos que en el problema de los dos cuerpos la siguiente cantidad es constante:

$$ \frac{v^2}{2}-\frac{\mu}{r}=\epsilon $$

Por otra parte usando la vis viva (Ec. vis_viva) encontramos que en el caso de órbitas no parábolicas, $e\neq 1$, el valor de la constante $\epsilon$ puede expresarse en términos del semieje mayor $a$ de la órbita como:

$$ \epsilon=-\frac{\mu}{2a} $$

En la última sección vimos sin embargo que en sistemas jerarquicos de N cuerpos, en los que se describe la dinámica como la superposición de N-1 subsistemas dos cuerpos, el valor los elementos orbitales de los subsistemas, incluyendo el semiejemayor $a$ puede cambiar en el tiempo. Si admitimos esto. el valor de $\epsilon$ en esos sistemas puede cambiar y lo hará a una tasa que puede expresarse como:

\begin{equation} \label{eq:dot_epsilon_preliminar} \dot{\epsilon}=\frac{\mu}{2a^2}\dot{a} \end{equation}

Esta ecuación esconde el secreto de la pregunta que nos hacíamos al final de la sección anterior: para calcular la variación de $a$ (y tal vez de otros elementos orbitales) es necesario calcular la variación de $\epsilon$ (Burns, 1976).

7.14.1. Perturbación del semieje mayor

Por el teorema de conservación de la energía (Teo. vis_viva) la tasa de variación en la energía mecánica de una partícula que esta sometida a una fuerza no conservativa $\vec F$ es:

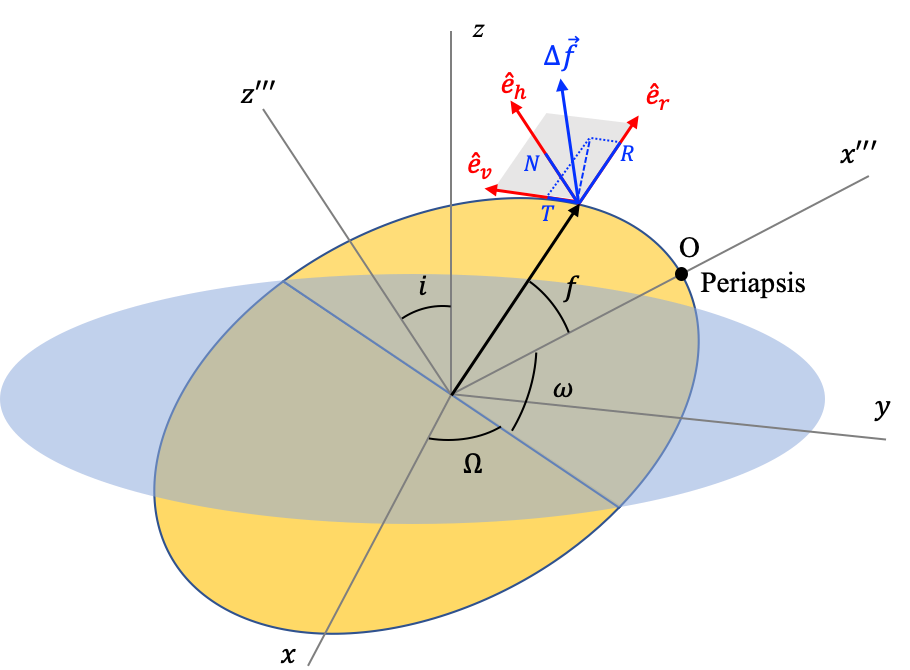
$$ \dot{E}=\dot{\vec r}\cdot \vec F $$

Supongamos que el sistema de dos cuerpos esta sometido a una fuerza (específica) neta externa $\Delta\vec f\ll -\mu{\vec r}/r^3$, que podemos escribir en términos de los vectores unitarios de coordenadas cilíndricas como:

$$ \Delta\vec f=R{\hat e}_r+T{\hat e}_v+N{\hat e}_h $$

Llamamo a $\Delta\vec f$ la fuerza perturbadora.

Fuerza perturbadora neta $

Figura 7.101. Fuerza perturbadora neta $

En términos de esta fuerza y del teorema de conservación de la energía, la variación en la energía específica se puede escribir como:

$$ \dot \epsilon=R\dot r + Tr{\dot f} $$

De otra parte, derivando la ecuación de la trayectoria (Ec. \label{eq:doscuerpos_trayectoria}):

$$ \dot r=\frac{pe{\dot f}\sin f}{1+e\cos f} $$

y usando el hecho de que sobre una cónica $r^2\dot f=\sqrt{\mu p}$, la variación de la energía relativa específica se puede escribir como:

\begin{equation} \label{eq:dot_epsilon} \dot \epsilon=\sqrt{\frac{\mu}{p}}\left[eR\sin f+T(1+e\cos f)\right] \end{equation}

Reemplazando en la Ec. (dot_epsilon_preliminar) y despejando $\dot a$ obtenemos finalmente:

\begin{equation} \label{eq:dot_a} \dot a=2\sqrt{\frac{a^3}{\mu(1-e^2)}}\left[eR\sin f+T(1+e\cos f)\right] \end{equation}

Como vemos solo las componentes radial y tangencial de la fuerza perturbadora pueden efectivamente cambiar el tamaño de la órbita. Las perturbaciones perpendiculaes al plano orbital no tienen un efecto sobre el tamaño, aunque sí sobre su orientación como veremos más adelante.

7.14.2. Perturbación de la excéntricidad

Si la energía relativa específica se altera por la acción de una fuerza perturbadora, la excentricidad de la órbita también será perturbada en virtud de la relación que ambas cantidades guardan de acuerdo con la Ec. (e_h_epsilon):

$$ e=\sqrt{1+\frac{2\epsilon h^2}{\mu^2}} $$

La tasa de cambio de $e$ será:

$$ \dot e=\frac{1}{2e}\left(2\frac{h^2{\dot\epsilon}}{\mu^2}+4\frac{\epsilon h{\dot h}}{\mu^2}\right) $$

Teniendo en cuenta que de acuerdo a la Ec. (e_h_epsilon):

$$ \frac{2\epsilon h^2}{\mu^2}=e^2-1 $$

la variación en la excentricidad se puede escribir como:

\begin{equation} \label{eq:dot_e_preliminar} \dot e=\frac{e^2-1}{2e}\left(\frac{\dot\epsilon}{\epsilon}+2\frac{\dot h}{h}\right) \end{equation}

La tasa de variación del momento angular específico se puede calcular con la ayuda de la torca (ver Sección Cantidades dinámicas):

$$ \dot{\vec h}=\vec r\times \Delta \vec f=rT\hat{e}_h-rN\hat{e}_v $$

Por otro lado si escribimos $\vec h=h\hat{e}_h$, y admitimos que la fuerza perturbadora puede cambiar la inclinación y orientación del plano, es decir $\dot{\hat{e}}_h\neq \vec o$:

$$ \dot{\vec h}={\dot h}{\hat e}_h+h\dot{\hat e}_h $$

La comparación de estas dos últimas ecuaciones permite escribir:

$$ \dot h=rT $$

Reemplazando esta expresión y la Ec. (dot_epsilon) en la Ec. (dot_e_preliminar) obtenemos finalmente:

\begin{equation} \label{eq:dot_e} \dot e=2\sqrt{\frac{a(1-e^2)}{\mu}}\left[eR\sin f+T(\cos f+\cos E)\right] \end{equation}

donde además hemos usado el hecho que $r=a(1-e\cos E)$.

Como sucedió con el tamaño, la forma de la órbita, parametrizada por la excentricidad $e$ no depende de la componente normal de la fuerza perturbadora.

7.14.3. Perturbaciones de la orientación

De manera análoga a como fueron deducidas en las secciones anteriores las tasas de cambio en el tamaño $a$ y la forma $e$ de la órbita osculatriz, es posible obtener ecuaciones para las tasas de cambio de los parámetros orbitales que describen su orientación en el espacio, $i$, $\Omega$ y $\omega$.

En aras de la brevedad y siendo esta sección apenas una introducción a la teoría de perturbaciones, reproducimos abajo las ecuaciones correspondientes. Una deducción detallada (y no muy difícil realmente) puede encontrarse en el artículo clásico de Burns (Burns, 1976) o en el reconocido texto de Murray y Dermott (Murray & Dermott, 1999).

La tasa de cambio de los parámetros de orientación de la órbita está dada por:

\begin{eqnarray} \label{eq:dot_i} \dot i & = & \sqrt{\frac{a(1-e^2)}{\mu}}\frac{\cos(\omega+f)}{1+e\cos f}N \\ \label{eq:dot_Omega} \dot \Omega & = & \sqrt{\frac{a(1-e^2)}{\mu}}\frac{\sin(\omega+f)}{\sin i(1+e\cos f)}N\\ \label{eq:dot_omega} \dot \omega & = & \frac{1}{e}\sqrt{\frac{a(1-e^2)}{\mu}}\left[-R\cos f+T\sin f\frac{2+e\cos f}{1+e\cos f}\right]-\dot\Omega\cos i \end{eqnarray}

Ecuación de la órbita osculatriz

En todas las ecuaciones anteriores aparecen explícitas las componentes de la fuerza perturbadora $\Delta\vec f$. Pero ¿dónde aparece en estas ecuaciones la fuerza central de magnitud $\mu/r^2$ que domina el movimiento relativo del sistema? El efecto de esta fuerza se ha hecho implícito al asumir, de un lado, que la ecuación de la trayectoria es:

$$ r=\frac{a(1-e^2)}{1+e\cos f} $$

y que instantáneamente se satisface la relación:

$$ h=r^2\dot f $$

Ambas ecuaciones son justamente el resultado de la integración de las ecuaciones de movimiento del problema relativo.

Despejando $\dot f$ en la última ecuación y usando la ecuación de la trayectoria escrita antes, podemos finalmente escribir la ecuación:

\begin{equation} \label{eq:dot_f} \dot f=\sqrt{\frac{\mu}{a^3(1-e^2)^3}}\;(1+e\cos f)^2 \end{equation}

En síntesis, las ecuaciones (dot_a), (dot_e), (dot_i), (dot_Omega), (dot_omega) y (dot_f), ofrecen una descripción completa del movimiento en el tiempo de un cuerpo sometido a una fuerza central con parámetro gravitacional $\mu$ y perturbado por una pequeña fuerza $\Delta\vec f=T\hat{e}_r+R\hat{e}_v+N\hat{e}_h$.

Estas ecuaciones constituyen un problema de valor inicial (IVP) en el que dados un conjunto de elementos orbitales iniciales $(a_0,e_0,i_0,\Omega_0,\omega_0,f_0)$ y una vez especificada la manera como las componentes de la fuerza perturbadora depende del estado del sistema, es posible calcular los elementos orbitales y de allí el estado del sistema en cualquier instante del tiempo futuro.

La implicaciones teóricas de estas ecuaciones están más allá del nivel de este libro y se desarrollan como parte de la teoría general de perturbaciones. En la siguiente sección ilustraremos, con la ayuda de las herramientas algoritmicas vistas en el libro, su aplicación en casos particulares.

7.14.4. Un ejemplo numérico

Consideremos por ejemplo el siguiente sistema jerarquico de tres cuerpos:

In [1]:
from numpy import array
sistema=[
    dict(
        m=1.0,
        r=array([0,0,0]),
        v=array([0,0.0,0]),
    ),
    dict(
        m=1e-8,
        r=array([1,1,0]),
        v=array([0.2,0.8,0.2]),
    ),
    dict(
        m=1e-5,
        r=array([2,0,0]),
        v=array([0,0.8,0]),
    ),    
]

#Trayectoria numérica
from numpy import linspace 
t0=0.0
T=100.0;Nt=1000
ts=linspace(t0,T,Nt)

from pymcel.export import ncuerpos_solucion
rs_num,vs_num,rps_num,vps_num,constantes=ncuerpos_solucion(sistema,ts)

#Grafíco
from pymcel.export import plot_ncuerpos_3d
fig=plot_ncuerpos_3d(rps_num,vps_num)

<Figure size 640x480 with 1 Axes>

Figura 7.102.

Como vemos en la Figura (code:ejemplo_sistema_perturbado) el sistema esta formado por una gran masa central (la partícula 0), rodeada de dos cuerpos, uno muy ligero (la partícula 1) que se encuentra en una órbita interior inclinada y otro de masa intermedia (la partícula 2) cuya órbita coincide aproximadamente con el plano $x-y$. Nos proponemos aquí predecir aproximadamente el movimiento de las partículas del sistema, usando la teoría de los dos cuerpos y la teoría básica de perturbaciones introducida en esta sección.

Como lo hicimos en secciones anteriores, lo primero que debemos hacer es identificar los subsistemas en los que puede descomponerse este sistema jerarquico. En la Figura (code:ejemplo_sistema_perturbado) reconocemos que se trata de un sistema central, usando las categoría que introdujimos en la Sección Motivación, que puede descomponerse en dos subsistemas:

  • Un sistema A formado por la partícula 0 (cuerpo central) y la partícula 1, la más liviana
  • Un sistema B formado por el cuerpo central y la partícula 2.

Usando la solución numérica a las ecuaciones de movimiento obtenidas en el Alg. (ejemplo_sistema_perturbado), podemos calcular y visualizar la evolución de los elementos orbitales del sistema A:

In [2]:
#Estado del sistema A
muA=sistema[0]["m"]+sistema[1]["m"]
r_A=rs_num[0,:]-rs_num[1,:]
v_A=vs_num[0,:]-vs_num[1,:]

#Calculo de los elementos orbitales
EAs=[]
for i,t in enumerate(ts):
    from spiceypy import oscelt
    EAs+=[oscelt(list(r_A[i])+list(v_A[i]),t,muA)]
from numpy import array
EAs=array(EAs)

#Gráfico
import matplotlib.pyplot as plt
fig,axs=plt.subplots(5,1,figsize=(5,8),sharex=True)
from numpy import pi

#Periapsis
axs[0].plot(ts,EAs[:,0])
axs[0].set_ylabel("$q$ (u.c.)")
#Excentricidad
axs[1].plot(ts,EAs[:,1])
axs[1].set_ylabel("$e$ (u.c.)")
#Inclinación
axs[2].plot(ts,EAs[:,2]*180/pi)
axs[2].set_ylabel("$i$ (grados)")
#Longitud del nodo ascendente
axs[3].plot(ts[:],EAs[:,3]*180/pi)
axs[3].set_ylabel("$\Omega$ (grados)")
#Argumento del periapsis
axs[4].plot(ts[:],EAs[:,4]*180/pi)
axs[4].set_ylabel("$\omega$ (grados)")

#Decoración
axs[0].set_title("Elementos orbitales partícula 1")
axs[-1].set_xlabel("$t$ (u.c.)")
fig.tight_layout()

Figura 7.103.

Como vemos en la Figura (code:ejemplo_sistemaA_perturbado) el movimiento de la partícula más ligera no es para nada Kepleriano. Sus elementos orbitales cambian sin una periodicidad reconocible y como producto de las perturbaciones producidas por la partícula masiva en la órbita externa.

Por su parte, una gráfica de la posición del sistema B (la partícula 2), pone en evidencia que su órbita es Kepleriana, al menos durante el tiempo de integración, y que los efectos perturbadores producidos por la presencia de la partícula 1 son despreciables:

In [3]:
#Estado del sistema B
muB=sistema[0]["m"]+sistema[2]["m"]
r_B=rs_num[0,:]-rs_num[2,:]
v_B=vs_num[0,:]-vs_num[2,:]

#Gráfico
import matplotlib.pyplot as plt
fig=plt.figure();
ax=fig.gca();
ax.plot(r_B[:,0],r_B[:,1]);

#
from pymcel.plot import fija_ejes_proporcionales
fija_ejes_proporcionales(ax,r_B);

Figura 7.104.

Así pues, la posición de la partícula 2 puede ser predicha con precisión usando únicamente la solución al problema de los dos cuerpos. Por su lado, para calcular la posición de la partícula 1 será necesario resolver el sistemas de ecuaciones diferenciales encontradas en la sección anterior.

Para hacerlo usando los métodos y herramientas que vimos en la Sección Ecuaciones diferenciales, es necesario primero escribir el sistema en la forma reducida (Ec. ecuaciones_reducidas) y para ello, debemos definir la identificación de las variables del sistema con las variables auxiliares $\{Y_i\}$. Una posible identificación es esta:

$$ Y_0=f, Y_1=a, Y_2=e, Y_3=i, Y_4=\Omega, Y_5=\omega $$

El aspecto más complicado de la implementación de las ecuaciones de perturbación es el cálculo de las componentes de la fuerza perturbadora. Para ello es necesario calcular, en cada momento, la posición de la partícula 2 y con ella la fuerza sobre la partícula 1:

$$ \Delta\vec f=-\frac{\mu_2}{r_{12}^3}{\vec r}_{12} $$

Las componentes de la fuerza perturbadora se pueden obtener proyectando el vector $\Delta\vec f$ sobre los vectores $\vec r$, $\vec v$ y $\vec h$:

\begin{eqnarray} \nonumber R & = & \frac{\Delta{\vec f}\cdot{\vec r}}{r}\\ \nonumber T & = & \frac{\Delta{\vec f}\cdot{\vec v}}{v}\\ \nonumber N & = & \frac{\Delta{\vec f}\cdot{\vec h}}{h}\\ \end{eqnarray}
In [4]:
from scipy.interpolate import interp1d
x_A_pred=interp1d(ts,r_A[:,0],kind='slinear')
y_A_pred=interp1d(ts,r_A[:,1],kind='slinear')
z_A_pred=interp1d(ts,r_A[:,2],kind='slinear')
vx_A_pred=interp1d(ts,v_A[:,0],kind='slinear')
vy_A_pred=interp1d(ts,v_A[:,1],kind='slinear')
vz_A_pred=interp1d(ts,v_A[:,2],kind='slinear')
X_A_pred=lambda t:array([x_A_pred(t),y_A_pred(t),z_A_pred(t),vx_A_pred(t),vy_A_pred(t),vz_A_pred(t)])
In [5]:
x_B_pred=interp1d(ts,r_B[:,0],kind='slinear')
y_B_pred=interp1d(ts,r_B[:,1],kind='slinear')
z_B_pred=interp1d(ts,r_B[:,2],kind='slinear')
vx_B_pred=interp1d(ts,v_B[:,0],kind='slinear')
vy_B_pred=interp1d(ts,v_B[:,1],kind='slinear')
vz_B_pred=interp1d(ts,v_B[:,2],kind='slinear')
X_B_pred=lambda t:array([x_B_pred(t),y_B_pred(t),z_B_pred(t),vx_B_pred(t),vy_B_pred(t),vz_B_pred(t)])
In [6]:
r_teo=[]
rP_teo=[]
def ecuaciones_lagrange(Y,t,mu,muP,mP,XP,verbose=0):
    global r_teo,rP_teo
    #Elementos orbitales
    f,a,e,i,W,w=Y
    if verbose:
        print(f"t = {t}")
        print(f"f = {f}")
        print(f"a,e = {a,e}")
        print(f"i,W,w = {i,W,w}")
    q=a*(1-e)
    p=a*(1-e**2)
    smup=sqrt(mu/p)
    if verbose:
        print(f"q = {q}")
        print(f"p = {p}")
        print(f"sqrt(mu/p) = {smup}")

    #Anomalía excéntrica
    from numpy import arctan
    E=2*arctan(sqrt((1-e)/(1+e))*tan(f/2))

    #Anomalía media
    from numpy import sin
    M=E-e*sin(E)
    
    if verbose:
        print(f"E = {E}")
        print(f"M = {M}")
        
    #Vector de estado instantaneo de la partícula
    from spiceypy import conics
    X=conics([q,e,i,W,w,M,t,mu],t)
    r=X[:3]
    v=X[3:]
    r_teo+=[r]
    if verbose:
        print(f"r = {r}")
        print(f"v = {v}")
    from numpy import cross
    hvec=cross(r,v)
    from numpy.linalg import norm
    h=norm(hvec)
    if verbose:
        print(f"hvec = {hvec} ({h})")
    
    #Vector de estado del perturbador
    from spiceypy import prop2b
    X=prop2b(muP,XP,t)
    rP=X[:3]
    vP=X[3:]
    rP_teo+=[rP]
    if verbose:
        print(f"mu_P = {muP}")
        print(f"r_P = {rP}")
        print(f"v_P = {vP}")
    
    #Fuerza perturbadora
    rrel=r-rP
    Deltaf=-mP*rrel/norm(rrel)**3
    if verbose:
        print(f"m_P = {mP}")
        print(f"r_rel = {rrel}")
        print(f"Delta f = {Deltaf}")
  
    #Componentes de la fuerza perturbadora
    from numpy import dot
    R=dot(Deltaf,r)/norm(r)
    T=dot(Deltaf,v)/norm(v)
    N=dot(Deltaf,hvec)/h
    if verbose:
        print(f"R = {R}")
        print(f"T = {T}")
        print(f"N = {N}")
    
    #Ecuaciones
    from numpy import cos
    dotf=sqrt(mu/(a**3*(1-e**2)**3))*(1+e*cos(f))**2
    if verbose:print(f"dotf={dotf}")
    dota=2*sqrt(a**3/(mu*(1-e**2)))*(e*R*sin(f)+T*(1+e*cos(f)))
    if verbose:print(f"dota={dota}")
    dote=1/smup*(R*sin(f)+T*(cos(f)+cos(E)))
    if verbose:print(f"dote={dote}")
    doti=1/smup*cos(w+f)*N/(1+e*cos(f))
    if verbose:print(f"doti={doti}")
    dotW=1/smup*sin(w+f)*N/(sin(i)*(1+e*cos(f)))
    if verbose:print(f"dotW={dotW}")
    dotw=1/(e*smup)*(-R*cos(f)+T*sin(f)*(2+e*cos(f))/(1+e*cos(f)))-dotW*cos(i)
    if verbose:print(f"dotw={dotw}")
    if verbose:print("--End--")
    return [dotf,dota,dote,doti,dotW,dotw]

Para integrar estas ecuaciones diferenciales debemos primero encontrar las condiciones iniciales:

In [7]:
#Elementos orbitales iniciales
qA,eA,iA,WA,wA,MA0,t0,muA=EAs[0]
aA=qA/(1-eA)

#Resuelve la ecuación de Kepler
from pymcel.export import kepler_newton
EA,error,ni=kepler_newton(MA0,eA,1e-14)

#Anomalía verdadera
from numpy import sqrt,arctan,tan
fA=2*arctan(sqrt((1+eA)/(1-eA))*tan(EA/2))

#Conficiones iniciales
Y0=[fA,aA,eA,iA,WA,wA]

#Vector de estado inicial del perturbador
muP=sistema[2]["m"]
XP=list(r_B[0])+list(v_B[0])

Condiciones iniciales del sistema A:
q = 0.23999201888165864
f = 145.7497370534556
E = 88.74633104932957
M = 41.007785890002175
a = 1.4404789013486834
e = 0.8333942839031101
i = 25.239401820678914
W = 45.0
w = 34.25026295986933
muP = 1e-05
XP = [-2.   0.   0.   0.  -0.8  0. ]

Usando el valor de estos elementos orbitales podemos finalmente escribir las condiciones iniciales y resolver las ecuaciones diferenciales de perturbación:

In [9]:
#iev=40;ecuaciones_lagrange(Y0,ts[iev],muA,muB,muP,XP,verbose=1)
from scipy.integrate import odeint
solucion=odeint(ecuaciones_lagrange,Y0,ts,args=(muA,muB,muP,XP))
from numpy import array
r_teo=array(r_teo)
rP_teo=array(rP_teo)

Una gráfica de la solución se muestra a continuación:

In [10]:
import matplotlib.pyplot as plt
fig,axs=plt.subplots(5,1,figsize=(5,8),sharex=True)

#Elementos
aes=solucion[:,1]
es=solucion[:,2]
qs=aes*(1-es)
ies=solucion[:,3]
Ws=solucion[:,4]
ws=solucion[:,5]

#Periapsis
axs[0].plot(ts,qs,label="Teoría Básica de Pert.")
axs[0].set_ylabel("$q$ (u.c.)")
axs[0].plot(ts,EAs[:,0],label="Numérico")
#Excentricidad
axs[1].plot(ts,es)
axs[1].set_ylabel("$e$ (u.c.)")
axs[1].plot(ts,EAs[:,1])
#Inclinación
axs[2].plot(ts,ies*180/pi)
axs[2].set_ylabel("$i$ (grados)")
axs[2].plot(ts,EAs[:,2]*180/pi)
#Longitud del nodo ascendente
axs[3].plot(ts[:],Ws*180/pi)
axs[3].set_ylabel("$\Omega$ (grados)")
axs[3].plot(ts[:],EAs[:,3]*180/pi)
#Argumento del periapsis
axs[4].plot(ts[:],ws*180/pi)
axs[4].set_ylabel("$\omega$ (grados)")
axs[4].plot(ts[:],EAs[:,4]*180/pi)
#Periapsis

#Decoración
axs[-1].set_xlabel("$t$ (u.c.)")
axs[0].legend(fontsize=8)
fig.tight_layout()

Figura 7.105.

Indice | Previo: Problema2Cuerpos.AproximacionJerarquico | Siguiente: Problema2Cuerpos.SPICE