Indice | Previo: Problema2Cuerpos.Motivacion | Siguiente: Problema2Cuerpos.OrbitaEspacio
7.2. El problema relativo de dos cuerpos¶
Naturalmente el problema de dos cuerpos es un caso particular del problema de los N cuerpos y la mayoría de las propiedades que descubrimos en el Capítulo El problema de los N cuerpos son válidas también en este caso.
Las ecuaciones de movimiento del sistema se reducen a (Ecs. edm_ncuerpos):
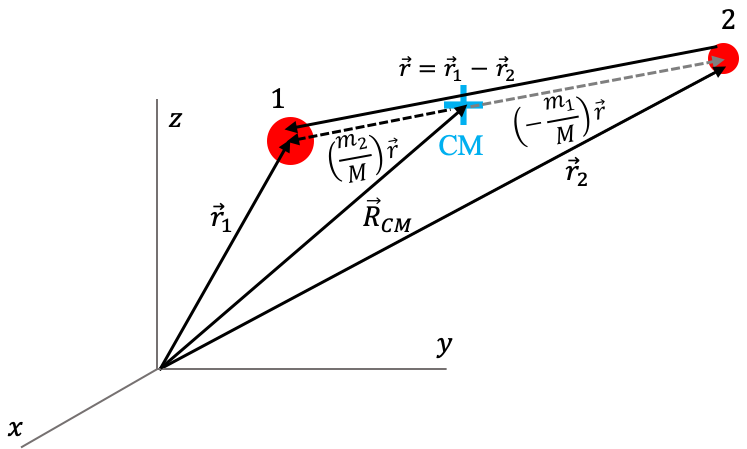
\begin{eqnarray} \label{eq:edm_doscuerpos} \ddot{\vec{r}}_1 & = & -\frac{\mu_2}{r_{12}^3}{\vec r}_{12} \\ \nonumber \ddot{\vec{r}}_2 & = & -\frac{\mu_1}{r_{21}^3}{\vec r}_{21} \end{eqnarray}donde ${\vec r}_{12}={\vec r}_1-{\vec r_2}=-{\vec r}_{21}$ (ver Figura (problema_dos_cuerpos).)
Al reducirse de orden, las Ecs. (edm_doscuerpos) corresponden a un total de 12 ecuaciones diferenciales ordinarias escalares de primer orden, con incognitas $x_1(t),y_1(t),z_1(t)$, ${\dot x}_1(t),{\dot y}_1(t),{\dot z}_1(t)$ y $x_2(t),y_2(t),z_2(t)$, ${\dot x}_2(t),{\dot y}_2(t),{\dot z}_2(t)$.
Las constantes de movimiento son las mismas que encontramos en la Sección ¿Solución analítica?:
- Tres para el momento lineal del centro de masa, Ec. (ncuerpos_momento).
- Tres para la posición inicial del centro de masa, Ec. (ncuerpos_centro_masa).
- Tres para el momento angular total, Ec. (ncuerpos_momento_angular)
- Una para la energía mecánica total, Ec. (ncuerpos_energia)
El problema tiene entonces, hasta ahora, tan solo 10 cuadraturas (constantes de movimientos) que relacionan algebraicamente 12 variables dependientes. Por lo tanto, si bien en esta caso el Teorema de Bruns generalizado, Teo. (ncuerpos_energia) no limita la posibilidad de encontrar otras constantes independientes, con la información disponible, el problema no puede resolverse por cuadraturas.
Hay sin embargo dos "simetrías" que reducen considerablemente el problema y nos ponen en el camino de una solución analítica completa.
La primera simetría la identificamos en la Sección Centro de masa y esta ilustrada en la Figura (problema_doscuerpos)). Habíamos mostrado que el centro de masa de un sistema de dos cuerpos esta siempre ocalizado sobre la línea que une las dos partículas. Esto implica que la posición de cada partícula puede expresarse como función de una sola cantidad vectorial, a saber, el vector relativo ${\vec r}\equiv{\vec r}_{12}$:
\begin{eqnarray} \label{eq:r1_r2_r} {\vec r}_1 & = & {\vec R}_\mathrm{CM}+\frac{m_2}{M} \vec r\\ \nonumber {\vec r}_2 & = & {\vec R}_\mathrm{CM}-\frac{m_1}{M} \vec r \end{eqnarray}y por consiguiente también la velocidad de las partículas es función solamente de la velocidad relativa entre ellas:
\begin{eqnarray} \label{eq:v1_v2_v} \dot{\vec r}_1 & = & \vec{V}_\mathrm{CM}+\frac{m_2}{M} \dot{\vec r}\\ \nonumber \dot{\vec r}_2 & = & \vec{V}_\mathrm{CM}-\frac{m_1}{M} \dot{\vec r} \end{eqnarray}Resolver el problema de los dos cuerpos consiste entonces, en realidad, en encontrar las funciones $\vec r(t)$ y $\dot{\vec r}(t)$ que describen el movimiento del vector relativo.
Para encontrar la e.d.m. del vector relativo, basta que restemos las Ecs. (edm_doscuerpos) y tengamos en cuenta que, por definición, $\ddot{\vec{r}} = \ddot{\vec{r}}_2 - \ddot{\vec{r}}_1$:
\begin{equation} \label{eq:edm_doscuerpos_relativo} \ddot{\vec{r}}=-\frac{\mu}{r^3}\vec{r} \end{equation}donde hemos introducido $\mu \equiv G(m_1+m_2)$ que llamaremos en lo sucesivo el parámetro gravitacional del sistema.
Con esta simetría, hemos reducido el tamaño del problema de las 12 ecuaciones diferenciales ordinarias de primer orden equivalentes a las Ecs. (edm_doscuerpos), a solo 6 ecuaciones (la versión reducida de la Ec. edm_doscuerpos_relativo), al costo, sin embargo, de abandonar las coordenadas originales y por la misma razón las cuadraturas que encontramos anteriormente.
Si queremos obtener la solución a este problema por el método de cuadraturas, debemos entonces encontrar 6 constantes de movimiento a partir de la Ec. (edm_doscuerpos_relativo) y que relacionen las 6 variables del problema: $x(t)$, $y(t)$, $z(t)$, $v_x(t)$, $v_y(t)$, $v_z(t)$.
7.3. Constantes de movimiento¶
Es claro que la Ec. (edm_doscuerpos_relativo), a diferencia de lo que paso en el problema de los N cuerpos con la Ec. (ncuerpos_suma_edm), no puede expresarse directamente en cuadraturas sin la ayuda de un factor integrante. Esto implica que en el problema relativo, a diferencia de lo que pasa en el problema de los N cuerpos, el momento lineal no es constante.
7.3.1. Momento angular específico relativo¶
Si pre multiplicamos ambos lados de la Ec. (edm_doscuerpos_relativo) por $\vec r\times$ obtenemos:
$$ \vec r\times \ddot{\vec r}=0 $$que puede expresarse en cuadraturas como:
$$ \frac{\mathrm{d}}{\mathrm{d}t} (\vec{r}\times \dot{\vec{r}}) = 0 $$de donde encontramos nuestro primera constante de movimiento:
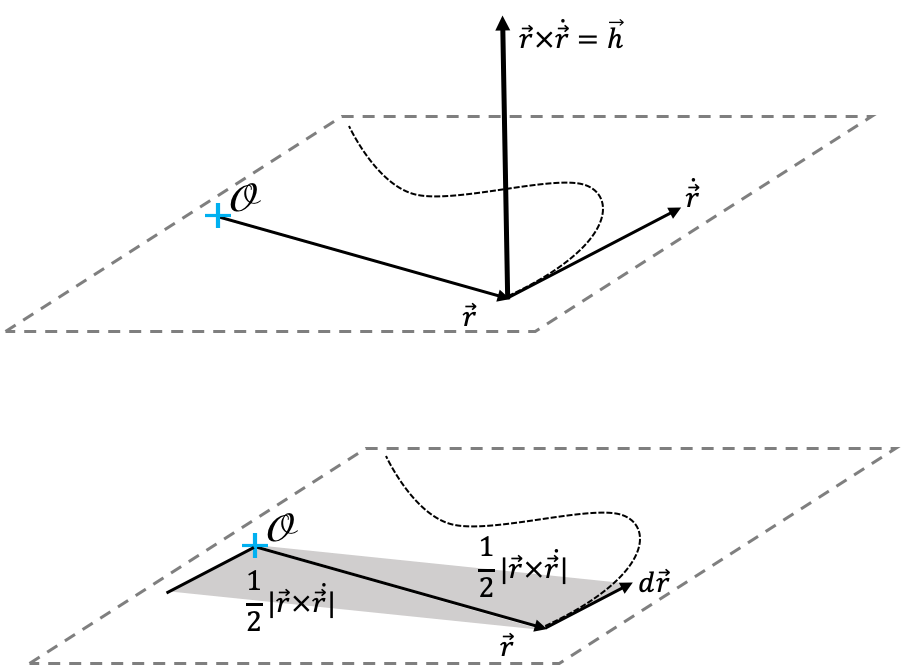
\begin{equation} \label{eq:h} \vec{r} \times \dot{\vec{r}}\equiv\vec{h} \end{equation}Si bien esta cantidad no se corresponde con ninguna cantidad dinámica del sistema original, su estructura y unidades nos recuerda la definición de un momento angular específico (momento angular por unidad de masa) y en lo sucesivo llamaremos a $\vec h$ el momento angular específico relativo del problema.
La constancia de la cantidad $\vec r\times\dot{\vec r}$ tiene una implicación mas trascendental aún. Como sucedió en el problema de los N cuerpos con el momento angular total referido al centro de masa, el vector constante $\vec h$ define un plano invariable, el análogo aquí del plano invariable de Laplace de la Def. (plano_orbital). Este plano, a diferencia del que encontramos en el problema de los N cuerpos, tiene una propiedad distintiva y crucial. Dado que por definición, el vector relativo $\vec r$ y su velocidad $\dot{\vec r}$ son perpendiculares a $\vec h$, ambos residiran siempre sobre ese plano (ver Figura (plano_orbital)). Como resultado, la trayectoria del vector relativo se realizará siempre sobre un plano (que en el sistema de referencia del centro de masa será invariable también.) Llamamos a este plano, el plano orbital del sistema.
La existencia de un plano orbital en el problema relativo de los dos cuerpos es una simetría nueva que reduce aún más el "tamaño" del sistema. Ahora, podemos escribir explícitamente el vector posición y el vector velocidad sobre el plano en términos de sus componentes en coordenadas cilíndricas (ver la Sección Sistemas de coordenadas), como:
\begin{eqnarray} \label{eq:r} \vec{r} & = & r\hat{a_r} \\ \label{eq:dotr} \dot{\vec{r}} & = & \dot{r}\hat{a_r} + r\dot{\theta} \hat{a_\theta} \end{eqnarray}y con esto el problema de los dos cuerpos relativo se reduce a encontrar las cuatro funciones $r(t)$, $\theta(t)$, $\dot{r}(t)$ y $\dot{\theta}(t)$ o sus equivalente cartesianos $x(t)$, $y(t)$, $\dot{x}(t)$ y $\dot{y}(t)$.
La magnitud del vector $\vec h$ tiene un significado adicional que viene directamente de la interpretación geométrica de la magnitud del producto cruz $2\mathrm{dA}=|\vec r\times \mathrm{d}{\vec r}|$ que no es otra cosa que el área del paralelogramo definido por los vectores $\vec r$ y $\mathrm{d}{\vec r}$ (ver Figura Figura (teorema_areas).):
$$ h=2\frac{\mathrm{d}A}{\mathrm{d}t} $$La constancia $h$ conduce a uno de los más conocidos teoremas de la mecánica celeste:
Proposición: Teorema de áreas. La velocidad areal del vector relativo (la razón de cambio del área barrida por el vector en su movimiento) en el problema de los dos cuerpos es constante e igual a:
\begin{equation} \label{eq:velocidad_areal} \frac{\mathrm{d}A}{\mathrm{d}t}=\frac{1}{2}h \end{equation}donde $h=|\vec r\times\dot{\vec r}|$.
En otros términos, el vector relativo en el problema de los dos cuerpos barre áreas iguales en tiempos iguales.
El teorema de áreas fue introducido originalmente en 1609 por Johanes Kepler en su obra cumbre "Astronomía Nueva". Kepler lo obtuvo por inducción (a diferencia de como lo hicimos aquí por deducción a partir de las ecuaciones de movimiento) con el objetivo específico de describir de la forma más precisa posible el movimiento del planeta Marte alrededor del Sol, del cual contaba con las observaciones precisas realizadas durante varias decadas por el astrónomo danés Tycho Brahe ("tico braja") Kepler, extendió este resultado "empírico" a todos los planetas, razón por la cual se lo conoce históricamente como la segunda ley del movimiento planetario.
Hay dos diferencias importantes entre la segunda ley de Kepler y el teorema de áreas formulado aquí. Mientras que la ley clásica aplica únicamente para el movimiento de planetas en trayectorias cerradas alrededor del Sol (que se asumía inmóvil) la versión moderna del teorema no hace ninguna suposición específica sobre la forma (si es cerrada o abierta) de la trayectoria del vector relativo. Adicionalmente, el teorema de áreas no dice nada sobre la relación entre las masas y se aplica universalmente a cualquier sistema de dos cuerpos, sea está la descripción (aproximada) el movimiento de un planeta alrededor del Sol, la de un cometa que sobrevuela a Júpiter o un sistema binario de estrellas de neutrones con masas similares
Formulado en términos de la velocidad areal, el teorema de áreas es relativamente oscuro. Si usamos la magnitud del vector $\vec h$ (Ec. \label{eq:h_escalar}) y escribimos:
\begin{equation} \label{eq:dotq} \dot\theta=\frac{h}{r^2} \end{equation}otra manera de interpretar la constancia del momento angular específico es decir que la velocidad angular $\dot\theta$ del vector relativo es mayor en tanto menor sea la magnitud el vector $r$ (distancia entre las partículas.) Es decir, las partículas del sistema se mueven más rapidamente en los puntos de máxima aproximación que en aquellos en los que están más lejos. Este comportamiento ya lo intuíamos al observar la solución numérica de los sistemas que estudiamos en el Capítulo El problema de los N cuerpos.
7.3.2. Energía específica relativa¶
Si pre multiplicamos ambos lados de la Ec. (edm_doscuerpos_relativo) por $\vec r\cdot$ obtenemos:
$$ \dot{\vec{r}} \cdot \ddot{\vec{r}} = -\frac{\mu}{r^3} \dot{\vec{r}} \cdot \vec{r}\\ $$que puede expresarse en cuadraturas como:
$$ \frac{d}{dt} \left(\frac{1}{2} \dot{\vec{r}}^2 \right)= \frac{d}{dt}\left(\frac{\mu}{r}\right) $$de donde encontramos una segunda constante de movimiento:
\begin{equation} \label{eq:epsilon} \frac{1}{2} \dot{\vec{r}}^2 - \frac{\mu}{r}\equiv\epsilon \end{equation}Si bien, como sucedió con $\vec h$, esta cantidad no se corresponde con ninguna cantidad dinámica del sistema original, su estructura y unidades nos recuerda la definición de una energía mecánica específica (energía mecánica por unidad de masa) y en lo sucesivo llamaremos a $\epsilon$ la energía específico relativa del problema.
De nuevo, teniendo en cuenta que el movimiento se realiza sobre un plano, la energía específica relativa se puede escribir en términos de las componentes cartesianas en la forma:
\begin{equation} \label{eq:epsilon_cartesianas} \frac{1}{2}({\dot x}^2+{\dot y}^2)-\frac{\mu}{\sqrt{x^2+y^2}}=\epsilon, \end{equation}o en coordenadas cilíndricas como:
\begin{equation} \label{eq:epsilon_cilindricas} \frac{1}{2}({\dot r}^2+r^2\dot{\theta}^2)-\frac{\mu}{r}=\epsilon \end{equation}donde al poner $\epsilon$ del lado derecho de la ecuación estamos reafirmando simbólicamente el hecho de que la fórmula del lado izquierdo es la que define explícitamente la cuadratura que puede, eventualmente, conducirnos a una solución exacta del problema. $\epsilon$ no es más que un número cuyo valor puede calcularse usando estas fórmulas por ejemplo a partir de las condiciones iniciales del problema.
Hasta aquí hemos conseguido dos cuadraturas del problema:
- La magnitud del momento angular específico relativo, Ec. (h_escalar), cuyo valor es $h$.
- La energía específica relativa, Ec. (epsilon_cilindricas), cuyo valor es $\epsilon$.
Si queremos resolver el problema por caudraturas necesitamos obtener cuatro constantes, el número de variables dependientes del problema relativo sobre el plano orbital. De acuerdo al Teorema de Bruns, para sistema con 3 o más cuerpos no hay ninguna otra constante de movimiento que sea independiente de las anteriores. En el problema relativo de los dos cuerpos, sin embargo, existe una constante nueva que nos permite resolver analíticamente el problema.
7.3.3. El vector de excentricidad¶
Que pasa si postmultiplicamos ambos lados de la Ec. (edm_doscuerpos_relativo) por $\times\vec h$:
$$ \ddot{\vec{r}}\times \vec{h} = -\frac{\mu}{r^3} \vec{r}\times \vec{h} $$Dado que $\vec h$ es constante, el lado izquierdo se puede escribir en cuadraturas:
\begin{equation} \label{eq:edmxh} \frac{\mathrm{d}}{\mathrm{d}t}(\dot{\vec{r}}\times \vec{h})=-\frac{\mu}{r^3} \vec{r}\times \vec{h} \end{equation}Por su parte en el lado derecho:
$$ \begin{array}{rcl} \vec{r}\times \vec{h} & = & \vec{r} \times (\vec{r} \times \dot{\vec{r}})\\ & = & \vec{r}(\vec{r}\cdot \dot{\vec{r}}) - \dot{\vec{r}}( \vec{r} \cdot \vec{r})\\ & = & \vec{r}r\dot{r} - \dot{\vec{r}}r^2 \end{array} $$que multiplicando por $-\mu/r^3$ también se puede escribir en cuadraturas como:
\begin{eqnarray} \nonumber \frac{\mu}{r^3}\vec{r}\times \vec{h} & = & -\mu \left(\frac{\vec{r}\dot{r}}{r^2} - \frac{\dot{\vec{r}}}{r}\right)\\ \nonumber & = & \frac{\mathrm{d}}{\mathrm{d}t}\left(\mu \frac{\vec{r}}{r} \right) \end{eqnarray}Con todo esto la Ec. (edmxh) en cuadraturas completas queda:
\begin{equation} \label{eq:cuadratura_e} \frac{\mathrm{d}}{\mathrm{d}t}(\dot{\vec{r}}\times \vec{h})=\frac{\mathrm{d}}{\mathrm{d}t}\left(\mu \frac{\vec{r}}{r} \right) \end{equation}y de aquí podemos identificar una nueva y complementamente independiente constante de movimiento:
\begin{equation} \label{eq:e} \frac{\dot{\vec{r}} \times \vec{h}}{\mu} - \frac{\vec{r}}{r}\equiv\vec{e} \end{equation}La razón por la que hemos expresado esta integral dividiendo la cuadratura en la Ec. (cuadratura_e) por $\mu$ es para hacer a la constante resultante adimensional (recordemos que $\mu$ tiene unidades de L$^3$/T$^2$) lo que es mas conveniente para su manipulación numérica.
¿Cuál es el significado geométrico o físico del vector $\vec e$? A diferencia de lo que pasó con $\vec h$ y con $\epsilon$, no es trivial encontrar ahora una cantidad dinámica que podamos asociar con $\vec e$. Este vector, sin embargo ha aparecido en distintos contextos en la historia de la física y las matemáticas, desde la mecánica celeste misma, pasando por el cálculo vectorial hasta la más reciente mecánica cuántica (ver recuadro Un poco de historia, Laplace, de la mecánica celeste a la mecánica cuántica.)
No es difícil mostrar que $\vec e$ no es enteramente independiente de $\vec h$ y $\epsilon$. Si se valcula la magnitud del vector se obtiene la relación (ver problemas al final del capítulo):
\begin{equation} \label{eq:e_h_epsilon} e=\sqrt{1+\frac{2\epsilon h^2}{\mu^2}} \end{equation}que será de gran utilidad en lo que queda de este capítulo y en general en la mecánica celeste.
7.4. La ecuación de la trayectoria¶
Una manera de encontrar una interpretación geométrica para el vector $\vec e$ es comparar su dirección con la de otros vectores en el plano orbital. Sabemos, por su definición en la Ec. (e) que $\vec e$ esta en el mismo plano que $\vec r$ y $\dot{\vec r}$. Si proyectamos $\vec e$ sobre el vector posición obtenemos:
$$ \vec{e}\cdot\vec{r} = \frac{1}{\mu}\vec{r} \cdot (\dot{\vec{r}} \times \vec{h}) - \vec{r}\cdot\frac{\vec r}{r} $$Utilizando la propiedad cíclica del tripe producto escalar (Ec. triple_producto_escalar) el primer término del lado derecho de la ecuación queda:
$$ \begin{array}{rcl} \vec{r} \cdot (\dot{\vec{r}} \times \vec{h}) & = & \vec{h} \cdot (\vec{r} \times \dot{\vec{r}})\\ & = & \vec{h} \cdot \vec{h} \\ & = & h^2 \end{array} $$de donde, la proyección es simplemente:
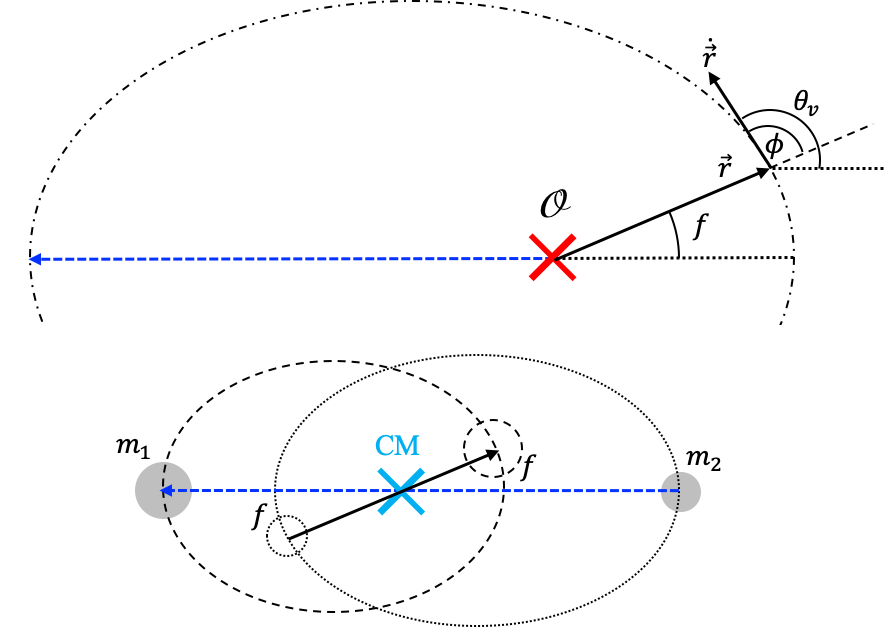
$$ \vec{e}\cdot\vec{r} = \frac{h^2}{\mu} - r $$Si ahora hacemos ${\vec e} \cdot {\vec r} = e r\cos \theta_{er}$, con $\theta_{er}$ el ángulo entre el vector $\vec e$ y el vector posición $\vec r$ sobre el plano orbital, la proyección se puede escribir como:
$$ e r\cos \theta_{er} = \frac{h^2}{\mu} - r $$de la que podemos despejar explícitamente $r$ en función de $\theta_{er}$:
\begin{equation} \label{eq:doscuerpos_trayectoria} r = \frac{h^2/\mu}{1 + e \cos \theta_{er}}, \end{equation}que es claramente la ecuación de una cónica con semilatus rectum, $p=h^2/\mu$, excentricidad $e=|\vec e|$ y anomalía verdadera $f=\theta_{er}$.
No solo hemos encontrado la interpretación geométrica para el vector $\vec e$ (el vector esta dirigido hacia el periapsis de la cónica y su magnitud es la excentricidad de la misma) sino que además encontramos con este sencillo procedimiento la forma general de la trayectoria descrita por el vector relativo en el problema de los dos cuerpos. Este resultado lo podemos formular como un teorema general:
Proposición: Primer teorema del movimiento orbital. El extremo del vector relativo en el problema de los dos cuerpos, describe en el plano orbital una trayectoria cónica con foco en el origen imaginario ${\cal O}$ (extremo del vector relativo), periapsis en la dirección del vector $\vec e=(\dot{\vec{r}} \times \vec{h})/{\mu} - {\vec r}/r$, excentricidad igual a $|\vec e|=\sqrt{1+2\epsilon h^2/\mu^2}$ y semilatus rectum $p=h^2/\mu$.
Este teorema es el equivalente moderno a la primera ley (empírica) de Kepler del movimiento planetario, formulada al mismo tiempo con su segunda ley (ver Teo. triple_producto_escalar) en 1609 en su texto "Astronomía nueva". A diferencia de la deducción realizada aquí, Kepler, después de estudiar el movimiento de Marte, esencialmente adivinó que su trayectoria debía ser una elipse. Adicionalmente y a diferencia de la primera ley de Kepler, el primer teorema del movimiento orbital formulado aquí no se restringe al caso de trayectorias elípticas, para las cuáles $|\vec e|<1$, sino que en principio predice que la trayectoria del vector relativo podría ser cualquier cónica incluyendo también una línea recta, una parábola o una hipérbola.
Un poco de historia: Laplace y el vector de excentricidad. Aunque pensamos normalmente que la solución al problema de los dos cuerpos fue obtenida por primera vez por Newton, en realidad la versión desarrollada aquí no es precisamente la que apareció en los Principia.
El primero en seguir el procedimiento y la notación mostrada aquí, usando para ello las constantes de movimiento en el problema, y en particular el vector de excentricidad, fue el científico estadoudinense Josiah Willard Gibbs (1839-1903.) Gibbs es además el padre de la notación vectorial que hemos usado y usaremos a lo largo de este texto, por lo que muchos de los resultados presentados aquí no tuvieron esta forma antes de 1870 cuando Gibbs escribió sus trabajos en el tema.
Gibbs había a su vez tomado la idea del vector de excentricidad de los trabajos del matemático alemám William Rowan Hamilton. En 1845, Hamilton publicó un artículo titulado "Aplicaciones de los cuaterniones en algunos problemas dinámicos" (los cuaterniones fueron inventados por Hamilton y precedieron a los vectores geométricos de Gibbs.) En este trabajo, el matemático alemán reportaba el descubrimiento de una nueva constante de movimiento en el problema de los dos cuerpos, precisamente el vector $\vec e$ de la Ec. (e).
Hoy sabemos que en realidad, Hamilton no había descubierto nada nuevo. La primera referencia conocida del vector de excentricidad se debe al matemático Francés Pierre-Simon Laplace (Goldstein, 1975). Es por esto que hoy al vector $\vec e$ (o en realidad versiones analogas al mismo) se lo conozca en algunos contextos como el vector de Laplace. Para ser justos deberíamos llamarlo el vector de Laplace-Hamilton. Si bien Laplace no uso exactamente la notación y el procedimiento mostrado en esta sección, es un hecho conocido que dedujo la forma que debía tener la órbita en el problema reducido de los dos cuerpos, manipulando el vector $\vec e$ de manera analoga a como lo hicimos aquí.
Laplace (1749-1827, ver Figura (laplace)) es una de las figuras más sobresalientes de las matemáticas, la física, la ingeniería y la astronomía de los 1700 y principios de los 1800. Los principios y problemas básicos de la mecánica celeste que fueron presentados y desarrollados por Newton y sus contemporáneos en términos geométricos, fueron traducidos enteramente en términos de cálculo infinitesimal (incluyendo la teoría de ecuaciones diferenciales) por Laplace, quién presentó a partir de 1799 una síntesis de todos los avances en el área que se habían realizado en los más de 100 que habían transcurrido desde la publicación de los Principia en 1687. El resultado fue un tratado de cinco volumenes titulado convenientemente Traité de mécanique céleste (Tratado de Mecánica Celeste o abreviado la Mecánica Celeste.)
La Mecánica Celeste de Laplace es considerado por muchos el libro más importante en el área escrito después de los Principia. Allí, además de la solución original al problema de los dos cuerpos presentada en esta sección, Laplace abordó la mayoría de los problemas centrales de la mecánica celeste, incluyendo algunos que Newton no había podido resolver: la teoría general de perturbaciones, la teoría general de mareas gravitacionales, el movimiento en campos gravitacionales producidos por cuerpos no esféricos, la estabilidad del sistema solar, entre muchos otros.
Muchos de los resultados en este libro y en la mayoría de los textos de mecánica celeste escritos en los últimos 200 años, son en realidad reelaboraciones modernas o aplicaciones de los resultados presentados en la Mecánica Celeste de Laplace.
Una cosa es el movimiento del vector relativo y otra la trayectoria que describen las partículas mismas en el espacio ¿son también esas trayectorias cónicas?
Usando las Ecs. (r1_r2_r) y la solución en la Ec. (doscuerpos_trayectoria) puede probarse que la distancia de cada partícula al centro de masa esta dada por:
\begin{eqnarray} \label{eq:doscuerpos_trayectoria_m1} r_1 & = & \frac{(m_2/M) h^2/\mu}{1 + e \cos f }\\ \label{eq:doscuerpos_trayectoria_m2} r_2 & = & \frac{(m_1/M) h^2/\mu}{1 + e \cos f }\\ \end{eqnarray}Este resultado implica las dos partículas tienen trayectorias cónicas con idéntica excentricidad, foco en el centro de masa y semilatus rectum proporcional a la distancia de cada una al centro de masa:
\begin{eqnarray} \nonumber p_1 & = & \frac{m_2}{M}p\\ p_2 & = & \frac{m_1}{M}p\\ \end{eqnarray}En la Figura (doscuerpos_trayectorias) mostramos un ejemplo de la trayectoria elíptica del vector relativo y las trayectorias correspondientes de las dos partículas.
7.5. La velocidad relativa¶
En la sección anterior mostramos que es posible, sin resolver el problema relativo de los dos cuerpos (es decir sin encontrar expresiones para la posición y velocidad relativa como función del tiempo), usar una de las cuadraturas (el vector de excentricidad) para escribir la ecuación en coordenadas cilíndricas de la trayectoria (Ec. doscuerpos_trayectoria.) Usando esa ecuación podemos encontrar el vector posición $\vec r:(r,\theta)$ para cualquier valor de $\theta$.
Ahora bien, ¿podemos, de forma análoga, saber cuál es el vector velocidad $\dot{\vec r}:(\dot r,r\dot \theta)$?
La magnitud del vector velocidad (rapidez) esta contenida en la energía específica relativa:
$$ \frac{v^2}{2}-\frac{\mu}{r}=\epsilon, $$de modo que si sabemos $\epsilon$ y $r$ (esté último se puede obtener con la Ec. ncuerpos_trayectoria) podemos obtener $v$.
De otro lado es posible, usando esta cuadratura escribir una expresión general para $\epsilon$ que será de mucha utilidad en lo sucesivo.
Para ello partimos de reconocer que podemos, para calcular el valor de la energía específica relativa, usar cualquier punto sobre la trayectoria. En particular, en el periapsis donde $r=q=a(1-e)$ (con $e\neq 1$) y $h=qv$, es decir $v=h/q$:
$$ \epsilon=\frac{h^2}{2a^2(1-e)^2}-\frac{\mu}{a(1-e)} $$Después de una sencilla manipulación algebraica obtenemos:
\begin{equation} \label{eq:e_mu_2a} \epsilon=-\frac{\mu}{2a} \end{equation}Esta expresión es válida únicamente en el caso en el que $e\neq 1$. En el caso de la parábola, $e=1$ puede mostrarse que $\epsilon=0$.
Si reemplazamos en la cuadratura de la energía específica relativa (Ec. epsilon) obtenemos:
\begin{equation} \label{eq:vis_viva} v^2=\mu\left(\frac{2}{r}-\frac{1}{a}\right) \end{equation}Donde de nuevo esta relación es válida únicamente si $e\neq 1$. Llamamos a esta relación la vis viva.
Una interesante propiedad de la vis viva es que dada una distancia relativa inicial $r$ y una rapidez relativa $v$, el valor del semieje mayor de la órbita resultante será independiente de la dirección de la velocidad:
$$ a=\frac{\mu}{2\mu/r-v^2} $$La vis viva nos permite calcular la magnitud de la velocidad, pero ¿cuál es la dirección de $\vec v$?
Podemos usar para ello el vector $\vec h$, cuya magnitud podemos escribir como:
$$ h=|\vec r\times \dot{\vec r}|=vr\sin\phi $$donde $\phi$ es el ángulo entre el vector posición y la velocidad (ver Figura (doscuerpos_trayectorias)) que llamaremos en lo sucesivo el argumento de la velocidad y que en virtud de la expresión anterior esta dado por:
\begin{equation} \label{eq:fi_conica} \sin\phi=\frac{h}{rv} \end{equation}Nota: Ángulo a partir de la magnitud del producto cruz. Aunque la Ec. (fi_conica) no tiene nunguna discusión, en la práctica el cálculo de $\phi$ a partir de ella tiene una sutileza. Dado que $h,r,v>0$ el signo de $\sin\phi$ siempre será positivo. Eso implicaría que $\phi<\pi/2$. Sin embargo si calculamos ahora el producto punto de $\vec r$ y $\dot{\vec r}$ (usando su definición en coordenadas cilíndricas, Sección Cantidades cinemáticas):
$$ cos\phi=\vec r\cdot\dot{\vec r}=r\dot{r} $$De aquí vemos que cuando $\dot{r}<0$, $\cos\phi<0$ y por tanto $\phi>\pi/2$. Es decir la Ec. (fi_conica) solo nos dará el valor correcto de $\phi$ cuando $\dot{r}\geq0$.
Pero, en términos de $r$ y $v$ ¿a qué condición corresponde $\dot{r}<0$?
Sabemos que cuando $0<f<\pi$, el vector relativo se estará alejando del periapsis, es decir ${\dot r}>0$. Del otro lado cuando $\pi<f<2\pi$ entonces ${\dot r}<0$. De aquí podemos deducir una fórmula, que si bien no es enteramente trivial, es lo mejor que podemos hacer para calcular el argumento de la velocidad en el cuadrante correcto:
\begin{equation} \phi = \left\{ \begin{array}{ll} \sin^{-1}\left(\frac{h}{rv}\right) & \mathrm{Si}\;0\leq f<pi\\ \pi-\sin^{-1}\left(\frac{h}{rv}\right) & \mathrm{Si}\;\pi\leq f<2pi\\ \end{array} \right. \end{equation}
Finalmente, el ángulo que forma la velocidad respecto a la dirección del periapsis (dirección del vector $\vec e$) estará dada por:
\begin{equation} \label{eq:tetav_conica} \theta_v = f+\phi \end{equation}7.6. El hodográfo del problema de los dos cuerpos¶
Hay una propiedad interesante que tiene el problema de los dos cuerpos. Fue descubierta por Hamilton (ver recuadro Un poco de historia) mientras estudiaba las consecuencias de describir el problema en términos vectoriales (en realidad usando cuaterniones, los antepasados de los vectores geométricos.)
Para conocer esta propiedad escribamos un algoritmo que nos permita calcular las componentes del vector veclocidad a lo largo de la trayectoria elíptica de un sistema de dos cuerpos ligado.
Supongamos para ello condiciones que nos garanticen que la cónica tiene periapsis sobre el semieje $x+$ (es decir $\vec e/e={\hat e}_x$). Si asumimos condiciones iniciales del tipo $\vec r_0=x_0{\hat e}_x$, $\dot{\vec r}_0=v_{0y}{\hat e}_y$, puede mostrarse que la condición anterior se cumple si $v_{0y}<\sqrt{\mu x_0}$ (ver problemas al final del capítulo.)
Un conjunto de condiciones iniciales que cumple esta condición es:
#Condiciones iniciales
mu=1 #unidades canónicas (u.c.)
from numpy import array
x0=1.0 #u.c.
vy0=0.5 #u.c.
#Magnitud de h
h=x0*vy0
#Energía específica relativa
from numpy.linalg import norm
epsilon=0.5*vy0**2-mu/x0
Usando las Ecs. (doscuerpos_trayectoria) y (e) podemos calcular las propiedades de la órbita descrita por el vector relativo:
#Parámetros geométricos derivados
from numpy import sqrt
p=h**2/mu
e=sqrt(1+2*epsilon*h**2/mu)
a=p/(1-e**2)
Comprobamos que efectivamente para las condiciones iniciales provistas la órbita resultante es una órbita elíptica ($e<1$.)
Calculemos ahora las componentes de la velocidad de la partícula a lo largo de la trayectoria, usando para ello la vis viva (Ec. vis_viva) y el argumento de la velocidad (Ecs. fi_conica y tetav_conica):
#Valores de la anomalía verdadera
from numpy import linspace,pi
fs=linspace(0,2*pi,100)
#Valores de r
from numpy import sin,cos
rs=p/(1+e*cos(fs))
#Valores de v
vs=sqrt(mu*(2/rs-1/a))
#Valores de phi
from numpy import arcsin,zeros_like
phis=zeros_like(fs)
for i,f in enumerate(fs):
if f<pi:
phis[i]=arcsin(h/(rs[i]*vs[i]))
else:
phis[i]=pi-arcsin(h/(rs[i]*vs[i]))
#Valores de tetav
from numpy import mod
tetavs=phis+fs
#Componentes de la velocidad
from numpy import sin
vxs=vs*cos(tetavs)
vys=vs*sin(tetavs)
Hagamos una gráfica del extremo de la velocidad relativa:
import matplotlib.pyplot as plt
fig=plt.figure()
ax=fig.gca()
#Grafica
ax.plot(vxs,vys,'r')
#Decoración
from pymcel.plot import fija_ejes_proporcionales
valores=(vxs,vys)
xrango,yrango=fija_ejes_proporcionales(ax,valores,xcm=0)
#Dibuja ejes
ax.plot(xrango,[0,0],'k-');
ax.plot([0,0],yrango,'k-');
ax.set_xlabel("$v_x$");
ax.set_ylabel("$v_y$");
A este gráfico se lo conoce en general como el hodografo. Como podemos apreciar, en el problema de los dos cuerpos el hodógrafo es una circunferencia descentrada, un resultado general que se puede formular como un teorema general (cuya demostración puede desarrollarse en la sección de problemas al final de este capítulo):
Proposición: El teorema del hodografo. El vector velocidad relativa en el problema de los dos cuerpos describe un círculo (hodografo) que tiene centro en $(0,\mu e/h)$ y radio $\mu/h$. Por la misma razón la ecuación paramétrica para la velocidad es:
\begin{equation} \label{eq:v_hodografo} \begin{array}{rcl} \dot x & = & -\frac{\mu}{h} \sin f\\ \dot y & = & \frac{\mu}{h} (e+\cos f)\\ \dot z & = & 0\\ \end{array} \end{equation}Este resultado es independiente de la cónica (independiente del valor de $e$).
7.7. El teorema armónico¶
En las secciones anteriores hemos usado las constantes de movimiento para deducir dos importantes teoremas sobre del problema relativo de los dos cuerpos que fueron descubiertas originalmente por Kepler y que se conocen históricamente como las leyes del movimiento planetario.
En 1619, Kepler publicó su libro "La armonía de los mundos" y en el revelo la que sería una de las más increíbles leyes del movimiento planetario (al menos para la época): la ley armónica. ¿Cuál es en términos modernos el teorema que corresponde a esta ley?
Proposición: Teorema armónico. Dado un sistema de dos cuerpos cuyo movimiento relativo es tal que $e\neq 1$, la velocidad angular promedio $n=\langle\dot\theta\rangle$ del vector relativo es independiente de la excentricidad de la órbita, y se relaciona con el valor absoluto del semieje mayor de la órbita relativa $|a|$ a través:
\begin{equation}\label{eq:teorema_armonico}n^2|a|^3 = \mu\end{equation}
Naturalmente esta no es la forma tradicional en la que conocemos la tercera ley de Kepler. Esta última fue formulada solo en el caso de movimiento sobre una órbita elíptica, mientras que el teorema general formulado arriba aplica también en el caso de órbitas hiperbólicas.
En realidad la ley armónica es un corolario del teorema de áreas. En el caso, por ejemplo, de una órbita elíptica, que es una órbita con período $T$, la velocidad areal se puede escribir como:
$$ \frac{\mathrm{d}A}{\mathrm{d}t}=\frac{A}{T}=\frac{\pi a b}{T} $$donde hemos aprovechado el hecho que la velocidad areal es constante para escribirla como la razón entre el área total de la elipse $A=\pi a b$ (Ec. area_elipse) y el período de la misma.
Si tenemos ahora en cuenta que $b=a\sqrt{1-e^2}$, $h^2=\mu a(1-e^2)$ y $\mathrm{d}A/\mathrm{d}t=h/2$ es fácil deducir que:
\begin{equation} \label{eq:ley_armonica} \frac{a^3}{T^2} = \frac{\mu}{4\pi^2} \end{equation}que es la forma original de la ley armónica de Kepler: "la razón entre el cubo del semiejemayor y el cuadrado del período orbital de los planetas es constante".
Lo que no sabía Kepler era la relación de esa constante con constantes física (la masa total del sistema) y geométricas (el factor $4\pi^2$.)
Para obtener a partir de la Ec. (ley_armonica) la relación entre $a$ y $n$ en el teorema armónico (Teo. ley_armonica), basta reconocer, de un lado, que en una órbita periódica la velocidad angular promedio es:
$$ n=\frac{2\pi}{T} $$y escribir la Ec. (ley_armonica) en la forma:
$$ a^3\left(\frac{2\pi}{T}\right)^2 = \mu $$Esta última es exactamente la relación $n^2a^3=\mu$ del teorema armónico.
En los problemas al final del capítulo el lector podrá demostrar el teorema armónico en el caso de una órbita hiperbólica.
7.8. Teoremas del movimiento orbital¶
Podemos finalmente sintetizar los resultados de esta sección enumerando en un mismo lugar los teoremas fundamentales del movimiento relativo de dos cuerpos:
Primer teorema del movimiento orbital (Teo. ley_armonica). El vector relativo de un sistema de dos cuerpos describe una trayectoria cónica.
Teorema de áreas (Teo. ley_armonica). La tasa de cambio del área barrida por el vector relativo es constante.
Teorema armónico (Teo. ley_armonica). El producto del cuadrado de la velocidad angular promedio del vector relativo y el cubo del valor absoluto del semiejemayor de su trayectoria es constante.
Hoy, por su importancia histórica, estos teoremas son todavía conocidos como las leyes del movimiento planetario de Kepler. Sin embargo, entre las versiones originales de las leyes formuladas por Kepler y las formas rigurosas de los teoremas presentadas aquí hay importantes diferencias. Por la misma razón en lo sucesivo y a través de todo este libro nos seguiremos refiriendo a estos resultados como los teoremas del movimiento orbital en lugar de llamarlos, como se acostumbra en todas partes, las leyes de Kepler.
Un poco de historia: Newton, Hooke y el primer teorema del movimiento orbital. Uno de los logros más significativos de la teoría del movimiento y la gravedad formulada por Newton en los 1680 y presentada en los Principia fue la demostración, que sintetizamos en esta sección usando métodos modernos, de que un cuerpo sometido a una fuerza central que varía con el inverso del cuadrado de la distancia se movería sobre una curva cónica.
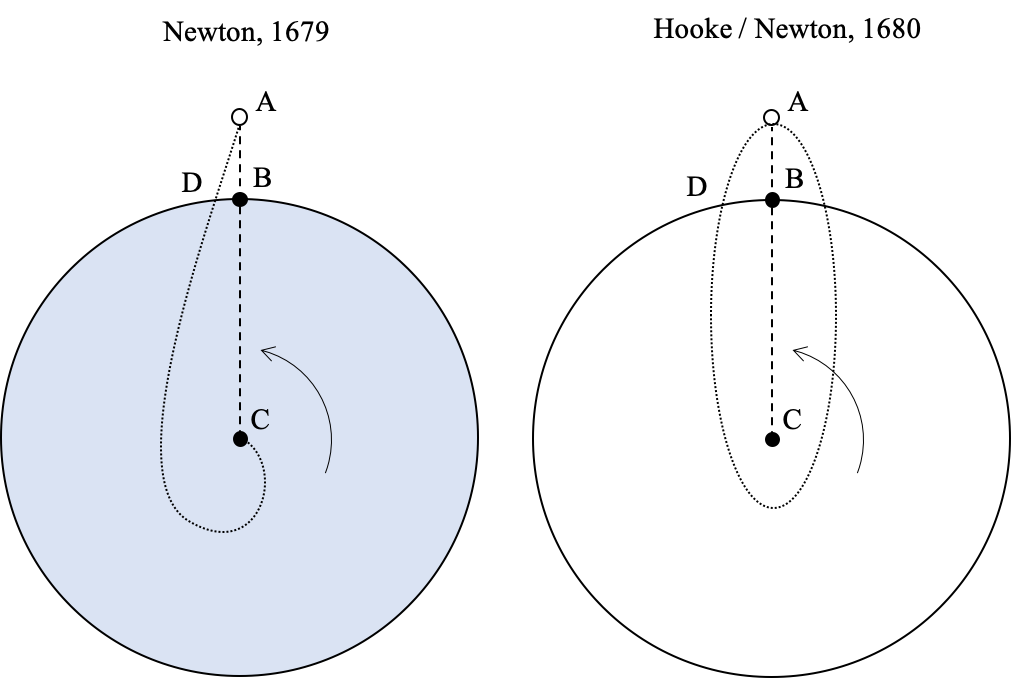
Como sucedió con la idea de la fuerza de gravedad, todo parece indicar que el primero en intuir esta relación fue Robert Hooke. En 1679, Newton, en respuesta a una carta previa de Hooke discutiendo el problema de la gravedad y la rotación de la Tierra, explicaba que contrario a lo que pensaban los escolásticos, quienes esgrimían contra la rotación de la Tierra la idea de que si un cuerpo se soltaba desde una cierta altura caería al oeste del punto de lanzamiento porque la Tierra debajo de él se habría movido hacia el oriente, en realidad por la ley de inercia el objeto caería un poco hacia el oriente: al lanzarse desde un punto más lejano del centro de la Tierra, su velocidad tangencial sería mayor que la velocidad de la superficie (ver Figura (hooke_newton).) Continuaba Newton explicando que si además el cuerpo pudiera moverse por dentro del planeta describiría, por efecto de la aceleración gravitacional una trayectoria en espiral hacia el centro.
Este sería uno de los poquísimos errores de intuición física que cometería Newton en público. La corrección del error le permitiría deducir con su teoría gravitacional, la primera ley de Kepler, pero también le costaría muchos dolores de cabeza en su debate público con Hooke por la prioridad en el descubrimiento.
Hooke respondió a Newton corrigiéndo en dos aspectos sus conclusiones sobre el experimento mental planteado. El primero era que si el cuerpo de su experimento se lanzaba en la latitud de Londrés en realidad caería hacia el sur oriente, esto porque la aceleración esta dirigida hacia el centro de la Tierra que desde la latitud de Inglaterra esta inclinado hacia al sur. La segunda y más crucial corrección fue, citando textualmente a Hooke "mi teoría del movimiento circular me hace suponer que [la trayectoria del cuerpo] sería algo muy diferente y en lo absoluto parecido a una espiral, sino más bien una especie de elipsoide." Hooke razonaba correctamente al mostrar que el movimiento de un cuerpo sometido a la atracción de la Tierra se movería de forma similar a un planeta alrededor del Sol.
Newton reconocería después que Hooke estaba en lo cierto, pero más importante, esta corrección lo motivo (como él mismo lo reconocío posteriormente) a verificar, usando el cálculo infinitesimal que había inventado unos años antes, si el movimiento sobre una elipse era compatible con una fuerza que variaba con el inverso del cuadrado de la distancia. Así lo hizo como quedo formulado en un teorema que presentó en un ensayo, anterior a los Principia pero que se convertiría en la semilla del Libro III del mismo, titulado De motu corporum in gyrum (Sobre los movientos de cuerpos en una órbita) y que fue leída por la Royal Society en 1684.
Hasta ahí todo se reduciría a explicar algo que se conocía desde los tiempos de Kepler. Pero una nueva teoría necesita predicciones enteramente nuevas. En diciembre de 1680 y enero de 1681 aparicieron en el cielo dos cometas casi idénticos (ver Figura (cometa_1680).) El astrónomo real John Flamsteed sostenía la teoría de que se trataba del mismo objeto que se había aproximado al Sol en 1680 y después había dado la vuelta "detrás" de él apareciendo en enero de 1681. Newton se intereso en la teoría de Flamsteed y recogió observaciones realizadas por él mismo, por el astrónomo real, por el italiano Giovanny Domenico Cassini y por su archienemigo Robert Hooke. Para 1682 Newton obtuvo finalmente la respuesta esperada: el cometa de 1680/1681 se movía en una trayectoría casi parabólica, producida por la atracción "magnética" del Sol y que, como la trayectoría elíptica, también obedecía la ley del inverso cuadrado de la distancia. La primera ley de Kepler se convertía así en el primer teorema del movimiento planetario formulado aquí.
Indice | Previo: Problema2Cuerpos.Motivacion | Siguiente: Problema2Cuerpos.OrbitaEspacio