Indice | Previo: Problema3Cuerpos.Motivacion | Siguiente: Problema3Cuerpos.CRTBP.Numerico
8.2. El problema restringido de los tres cuerpos¶
En los sistemas mencionados en la sección anterior, incluyendo aquel cuya dinámica simulamos explícitamente, siempre consideramos dos partículas grandes que forman un sistema de dos cuerpos (por ejemplo el Sol y la Tierra), y una tercera partícula (un vehículo espacial) con una masa mucho más pequeña que las dos primeras.
Dado que la partícula más liviana ($m_0$) ejerce un efecto despreciable sobre el movimiento de las partículas más masivas ($m_1$ y $m_2$), la posición y velocidad de estas últimas puede obtenerse usando las fórmulas y procedimientos descritos en el Capítulo El problema de los dos cuerpos. De este modo el problema resultante consiste simplemente en la predicción de las posiciones y velocidades de $m_0$. La descripción completa de un sistema así es a lo que llamaremos aquí el problema restringido de los tres cuerpos.
Las ecuaciones de movimiento de la partícula $m_0$ serán:
\begin{equation} \label{eq:rtbp_general} \ddot{\vec{r}}_0(t) = -\frac{\mu_1}{r_{01}^3}\vec{r}_{01} -\frac{\mu_2}{r_{02}^3}\vec{r}_{02} \end{equation}donde $\vec r_{01}=\vec r_0-\vec r_1$ y $\vec r_{02}=\vec r_0-\vec r_2$ y los parámetros gravitacionales $\mu_1=Gm_1$ y $\mu_2=Gm_2$.
Dado que ahora es prácticamente irrelevante numerar a la única partícula de interés en el sistema (la partícula 0), en lo sucesivo nos referirnos a su posición y velocidad como $\vec r(t)\equiv \vec r_0(t)$, $\dot{\vec r}(t)\equiv\dot{\vec r}_0(t)$, y a su posición relativa respecto a las dos partículas más masivas como $\vec r_1\equiv\vec r_{01}$ y $\vec r_2\equiv\vec r_{02}$. De este modo la ecuación de movimiento (Ec. rtbp_general) queda:
\begin{equation} \label{eq:rtbp} \ddot{\vec{r}}(t) = -\frac{\mu_1}{r_{1}^3}\vec{r}_{1} -\frac{\mu_2}{r_{2}^3}\vec{r}_{2} \end{equation}Dado que el movimiento del sistema formado por las partículas más masivas (1 y 2) se realiza sobre un plano (problema de los dos cuerpos), la mejor elección del sistema de coordenadas será aquella en la que el plano $x-y$ reside sobre el plano orbita de 1 y 2, y el eje $x$ apunta en dirección al periapsis del sistema. En este sistema de referencia podemos escribir explícitamente las cantidades de la Ec. (rtbp) como:
\begin{equation} \label{eq:rtbp_r1_r2} \begin{array}{rcl} \vec{r}_1 & = & (x-x_1)\hat e_x + (y-y_1)\hat e_y + z\hat e_z\\ \vec{r}_2 & = & (x-x_2)\hat e_x + (y-y_2)\hat e_y + z\hat e_z\\ \end{array} \end{equation}Ciertamente la complejidad del problema restringido, planteado de esta manera, se ha reducido considerablemente respecto al problema general de tres cuerpos. Pasamos, por ejemplo, de tener con 18 variables independientes (posiciones y velocidades de las tres partículas) y 3 ecuaciones vectoriales, a solo 6 variables (posición y velocidad de la partícula más ligera) y una ecuación diferencial (Ec. rtbp).
Aún así las cantidades $x_1(t)$, $y_1(t)$, $x_2(t)$, $y_2(t)$ que aparecen impplícitamente en la ecuación a través de las expresiones para $\vec r_1$ y $\vec r_2$ (Ecs. rtbp_r1_r2), no se pueden escribir como funciones elementales del tiempo (implícitamente es necesario resolver la Ecuación de Kepler), de modo que la solución a la ecuación de movimiento (Ec. rtbp) solo parece posible a través de procedimientos numéricos. Si ese es el caso, lo único que habremos conseguido hasta ahora fue reducir la complejidad del problema numérico, pero sin ganar comprensión del problema físico de fondo.
¿Cómo podemos "deshacernos" de la limitación impuesta por las variables $x_1(t)$, $y_1(t)$, $x_2(t)$, $y_2(t)$?
Una manera de hacerlo sería considerar solo aquellas situaciones en las que estas cantidades obedezcan las expresiones más simples posibles; es decir considerar el problema solo en el caso en el que el movimiento de los cuerpos más masivos sigan las trayectorias más elementales admisibles en el problema de los dos cuerpos.
8.3. El problema circular restringido de los tres cuerpos (CRTBP)¶
El caso más simple resulta al asumir que los cuerpos más masivos se mueven siguiendo trayectorias circulares alrededor de su centro de masa común (o equivalentemente, que el movimiento relativo es elíptico con excentricidad 0). Al problema resultante de describir el movimiento de una partícula de masa despreciable, respecto a dos cuerpos que se mueven en orbitas circulares relativas, lo conocemos como el problema circular restringido de los dos cuerpos (CRTBP por las siglas en inglés de circular restricted three body problem).
En esta situación, la posición de las partículas más masivas se puede describir analíticamente como:
\begin{equation} \begin{array}{rcl} x_1 & = & -a_1 \cos (n t) \\ y_1 & = & -a_1 \sin (n t) \\ x_2 & = & +a_2 \cos (n t) \\ y_2 & = & +a_2 \sin (n t) \\ \end{array} \end{equation}donde $a_1=(m_2/M) a$, $a_2=(m_1/M) a$ (ver Ecs. a1_a2), con $M=m_1+m_2$. Por otro lado $n=\sqrt{\mu/a^3}$ es la velocidad angular del vector relativo, $\mu=G M$ y $a$ es el semieje mayor de la órbita relativa de los cuerpos $m_1$ y $m_2$.
Como puede verse $a$ es el único parámetro geométrico relevante y, junto con $\mu$, determinan completamente la posición de las partículas más masivas en el sistema.
Conocer la forma analítica de las posiciones de las partículas masivas es un gran paso. Sin embargo la ecuación de movimiento resultante (Ec. rtbp) sigue siendo tan complicada que es poco lo que podremos ganar analizándola con las técnicas que hemos utilizado en el texto (solución por cuadraturas).
Existe sin embargo un recurso ingenieoso y que ofrece las oportunidades que necesitamos para ganar alguna comprensión del sistema, sin resolver numéricamente las ecuaciones de movimiento.
Hasta ahora, nos habíamos ocupado de estudiar los problemas del movimiento relativo de partículas en sistemas de dos o más cuerpos, en sistemas de referencia inerciales. Pero ¿qué pasa si usamos un sistema de referencia no inercial convenientemente construído?
Ya en la Sección Dinámica en sistemas de referencia rotantes habíamos mostrado como formular y resolver las ecuaciones de movimiento de partículas en sistemas no inerciales, en particular en sistemas de referencia rotantes.
En el caso del crtbp, por ejemplo, podemos estudiar el movimiento de la partícula de prueba en un sistema de referencia no inercial que rote de modo que las partículas más masivas se mantengan en reposo. Para lograrlo basta que la velocidad angular del sistema de referencia sea igual a $n$, es decir que $\omega=n$ (ver Sección Dinámica en sistemas de referencia rotantes).
En un sistema de referencia como este las coordenadas de las partículas masivas se hacen las más simples posible:
\begin{eqnarray} \nonumber x_1 & = & -\frac{m_2}{M} a \\ \nonumber y_1 & = & 0 \\ \nonumber x_2 & = & +\frac{m_1}{M} a \\ \nonumber y_2 & = & 0 \\ \end{eqnarray}A pesar de esta simplificación, la ecuación de movimiento se hace más complicada: además de las aceleraciones debidas a las interacciones gravitacionales de la partícula de prueba con las partículas masivas que incluimos en la Ec. (rtbp), en el sistema rotante debemos agregar las aceleraciones no inerciales, aceleración centrífuga, aceleración de coriolis (la aceleración de Euler en este caso sera cero), cuyas formas explícitas dedujimos en la Sección Dinámica en sistemas de referencia rotantes.
La ecuación de movimiento en este sistema de referencia se escribirá como:
\begin{equation} \label{eq:crtbp} \ddot{\vec{r}} = -\frac{\mu_1}{{r_{1}}^3}\vec{r}_{1} -\frac{\mu_2}{r_{2}^3}\vec{r}_{2} -\vec{\omega}\times(\vec{\omega}\times \vec{r}) -2\vec{\omega}\times \dot{\vec{r}} \end{equation}donde $\vec\omega\equiv\omega \hat{e}_z$.
Aquí es muy importante aclarar que tanto la aceleración $\ddot{\vec{r}}$, la velocidad $\dot{\vec{r}}$ y las posiciones relativas $\vec{r}_{1}$ y $\vec{r}_{2}$ son las del sistema rotante (las que "primamos" en la Sección Dinámica en sistemas de referencia rotantes). Si no hacemos aquí la distinción entre estas cantidades y aquellas del sistema inercial (que son las que usamos en la Ec. rtbp) es por cuestión de simplicidad y espacio. Esta distinción, sin embargo debe tenerse cuidadosamente en cuenta, cuando vayamos a implementar estas ideas en algoritmos.
8.4. Las unidades canónicas del CRTBP¶
Hay una interesante simplificación de las ecuaciones de movimiento que se produce por la simple elección de un sistema de unidades apropiado.
Si, como es costumbre, escogemos un sistema de unidades en el que $G=1$, $U_M=M=m_1+m_2$ y $U_L=a$, entonces, en este sistema de coordenadas:
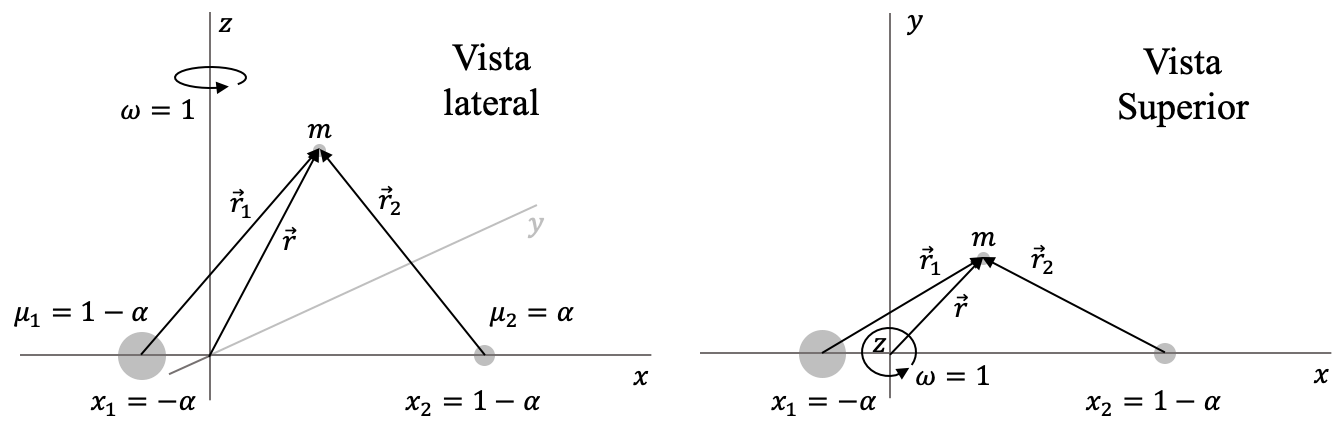
- $\omega=n=\sqrt{\mu/a^3}=1$.
- Si llamamos $\alpha\equiv \mu_2$, entonces $\mu_1 = \mu - \mu_2=1-\alpha$.
- $x_1=-\alpha$ y $x_2=1-\alpha$.
En este sistema de unidades las ecuaciones de movimiento (Ec. crtbp) se pueden escribir ahora como:
\begin{equation} \label{eq:crtbp_uc} \ddot{\vec{r}} = -(1-\alpha)\frac{\vec{r}_{1}}{{r_{1}}^3} -\alpha\frac{\vec{r}_{2}}{r_{2}^3} -\hat{e}_z\times(\hat{e}_z\times \vec{r}) -2\hat{e}_z\times \dot{\vec{r}} \end{equation}con:
\begin{eqnarray} \vec r_1 & = & (x+\alpha)\hat e_x + y\hat e_y + z\hat e_z\\ \vec r_2 & = & (x+\alpha-1)\hat e_x + y\hat e_y + z\hat e_z\\ \end{eqnarray}Con todas las restricciones implícitas en la Ec. (crtbp_uc) podemos finalmente proceder a estudiar esta ecuación con los métodos vistos en capítulos anteriores para de este modo ganar intuición sobre el comportamiento de este tipo de sistemas.
Indice | Previo: Problema3Cuerpos.Motivacion | Siguiente: Problema3Cuerpos.CRTBP.Numerico