Indice | Previo: Mecanica.Dinamica.SistemaParticulas | Siguiente: Mecanica.SistemasNoInerciales.Numerico

5.5. Dinámica en sistemas de referencia no inerciales

Todas los postulados y teoremas que describen la dinámica de partículas y sistemas de partículas introducidos en las secciones anteriores, tienen validez, como se expreso desde el principio, en sistemas de referencia inerciales (ver Def. K_sistema_ejemplo).

¿Cómo se modifican (si se modifican) esos postulaods y teoremas si por necesidad o "construcción" es necesario describir la dinámica de una partícula o un sistema de partículas respecto de un sistema de referencia no inercial?

Suponga por ejemplo que queremos describir la dinámica del vuelo de un cohete respecto a la superficie de la Tierra. Si bien es posible pasarnos al sistema de referencia del centro del planeta (que es aproximadamente inercial), por razones prácticas es preferible, al menos al principio del movimiento, describir las cantidades cinemáticas y dinámicas del cohete respecto a la plataforma de lanzamiento o bien a la superficie alrededor de ella. Un sistema de referencia fijado así, ya no puede considerarse un sistema de referencia inercial (debido a la rotación de la Tierra).

Suponga ahora que un astronauta quiere hacer un experimento mecánico en el interior de la estación espacial internacional. Naturalmente allí, será mejor referir las cantidades cinemáticas y dinámicas a la estructura de la estación y no al centro de la tierra. De nuevo, para hacerlo deberá trabajar en un sistema de referencia no inercial.

Estos dos ejemplos sencillos muestran que si bien es más común (y mucho más conveniente en general) aplicar los postulados y teoremas de la mecánica en sistemas de referencia inerciales (donde han sido desarrollados y demostrados) habrán situaciones en las que se hace obligatorio hacerlo en sistemas de referencia no inerciales.

5.5.1. Transformación entre sistemas de referencia

En la Sección Sistemas de referencia habíamos introducido las denominadas transformaciones de Galileo que son el conjunto de reglas matemáticas necesarias para convertir las cantidades cinemáticas o dinámicas $t$, $\vec r$, $\vec v$, $\vec a$, etc. medidas en un sistema de referencia inercial $R$, en el valor de las mismas cantidades en otro sistema de referencia inercial $R'$ (ver Definición K_sistema_ejemplo).

Las reglas que postulamos allí eran bastante sencillas:

\begin{equation} \label{eq:transformaciones_galileo} \begin{array}{rcl} t & = & t'\\ \vec r & = & \vec{r}' + \vec u t \end{array} \end{equation}

Para extender estas reglas al dominio de la dinámica, podemos agregar el postulado de que la masa de las partículas es también independiente del sistema de referencia en el que se la mida:

\begin{equation} m = m' \end{equation}

Este postulado se basa en la idea Newtoniana de que la masa es, entre otras, una medida de la cantidad de materia contenida en un cuerpo, que no debería depender del observador que la juzgue.

Todos los postulados y teoremas de la dinámica que formulamos en este capítulo son válidos unicamente si se expresan en las cantidades cinemáticas y dinámicas que satisfacen estas transformaciones y aquellas que se derivadan de ellas (como la regla de adición de velocidades y aceleraciones de las Ecs. ley_adicion_velocidades y ley_adicion_aceleraciones).

¿Qué pasa ahora si admitimos la posibilidad de que el sistema $R'$ se mueva respecto a $R$ (que seguiremos asumiendo incercial) con una velocidad $u(t)$ que no es constante (el sistema no es inercial)?

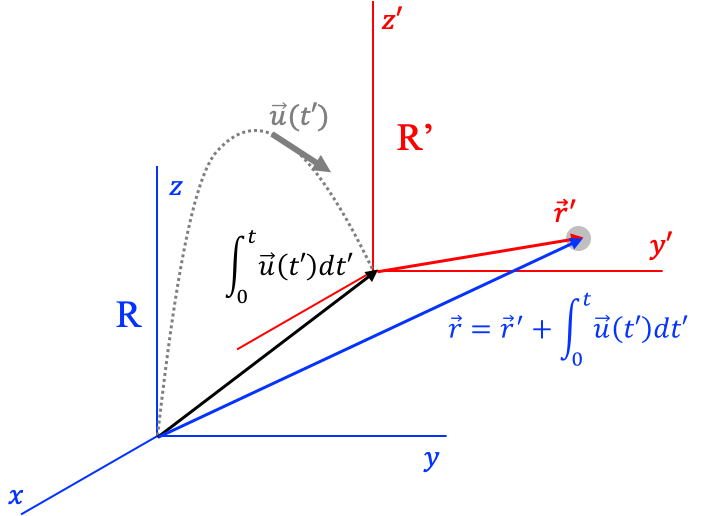
Una generalización trivial de las transformaciones de Galileo es (ver Figura (transformaciones_noinercial)):

\begin{equation} \label{eq:transformaciones_acelerado} \begin{array}{rcl} t & = & t'\\ \vec r & = & \vec{r}' + \int_0^t \vec u(t)\;\mathrm{d}t\\ m & = & m'\\ \end{array} \end{equation}

en la que hemos asumido que la dirección de los ejes coordenados de los sistemas se mantiene paralela a lo largo del tiempo.

Figura 5.52. Construcción geométrica para deducir la regla de transformación de la posición $

Usando estas transofrmaciones básicas, es posible deducir las reglas de transformación para otras cantidades cinemáticas y dinámicas. Así por ejemplo:

\begin{eqnarray} \label{eq:v_no_inercial} \vec{v}' & = & \vec{v}-\vec u(t)\\ \label{eq:p_no_inercial} \vec{p}' & = & \vec{p}-m\vec u(t)\\ \label{eq:a_no_inercial} \vec{a}' & = & \vec{a}-\dot{\vec u}\\ \label{eq:F_no_inercial} \vec{\cal F}' & = & \vec{\cal F}-m\dot{\vec u} \end{eqnarray}

Estas transformaciones nos permiten comprobar cómo se modifica la validez de los postulados de la dinámica y de los teoremas defivados de ellos, al pasar a un sistema de referencia no inercial.

Considere por ejemplo el caso de una partícula que se mueve libre de fuerzas aplicadas, y por tanto que tiene, en el sistema de referencia inercial $R$, velocidad $\vec v$ (o momentum lineal $\vec p$) constantes (obedenciendo el teorema de inercia). Según la regla de transformación en la Ec. (v_no_inercial), la velocidad $\vec{v}'$ de la partícula en el sistema no inercial $R'$ (y por lo tanto su momentum lineal $\vec{p}'$) ya no serán constantes: su valor dependerá de la velocidad instantánea del sistema $R'$ respecto de $R$, $u(t)$, que a su vez cambia en el tiempo. El teorema de inercia ya no es válido en $R'$. Es justamente por esto que decimos que $R'$ es un sistema de referencia no inercial.

Un caso partícular de esta última situación, pone de relieve los aparentemente extraños comportamientos que podríamos percibir en sistemas de referencia no inerciales. La misma partícula del párrafo anterior, dejada en reposo en $R$ en $t$ (y que se mantendría en reposo respecto a $R$ en virtud del teorema de inercia), empezará a moverse con velocidad $-\vec u(0)$ respecto a $R'$ sin que se aplique sobre ella ninguna fuerza.

Este tipo de comportamientos es el que explica, por ejemplo, porque una persona que no se sostiene de las barandas del Metro en el momento en el que inicia su marcha, empezará a desplazarse, sin que nada o nadie actúe sobre ella en el interior del vagón.

Así mismo, incluso en la presencia de fuerzas aplicadas, el postulado de fuerzas no será válido en el sistema de referencia $R'$. Según este postulado, en el sistema de referencia inercial ($R$) la fuerza resultante sobre una partícula es iguales a la fuerza aplicada neta:

$$ \vec{\cal F} = \vec F $$

o lo que es lo mismo:

$$ \vec{a} = \frac{\vec F}{m} $$

De acuerdo a la Ec. (F_no_inercial) en el sistema de referencia no inercial:

\begin{equation} \label{eq:F_aplicada_no_inercial} \vec{\cal F}' = \vec F - m\dot{\vec u} \end{equation}

o bien

$$ \vec{a}' = \frac{\vec F}{m} - \dot{\vec u} $$

Es decir, las fuerzas resultantes en el sistemas de referencia no inercial, serán iguales a las fuerzas aplicadas más una fuerza resultante $-m\dot{\vec u}$ que apunta en dirección contraria a la aceleración relativa entre los sistemas de referencia. Dado que esta fuerza resultante nueva no es producto de la acción de una fuerza aplicada, la llamamos convencionalmente una fuerza ficticia.

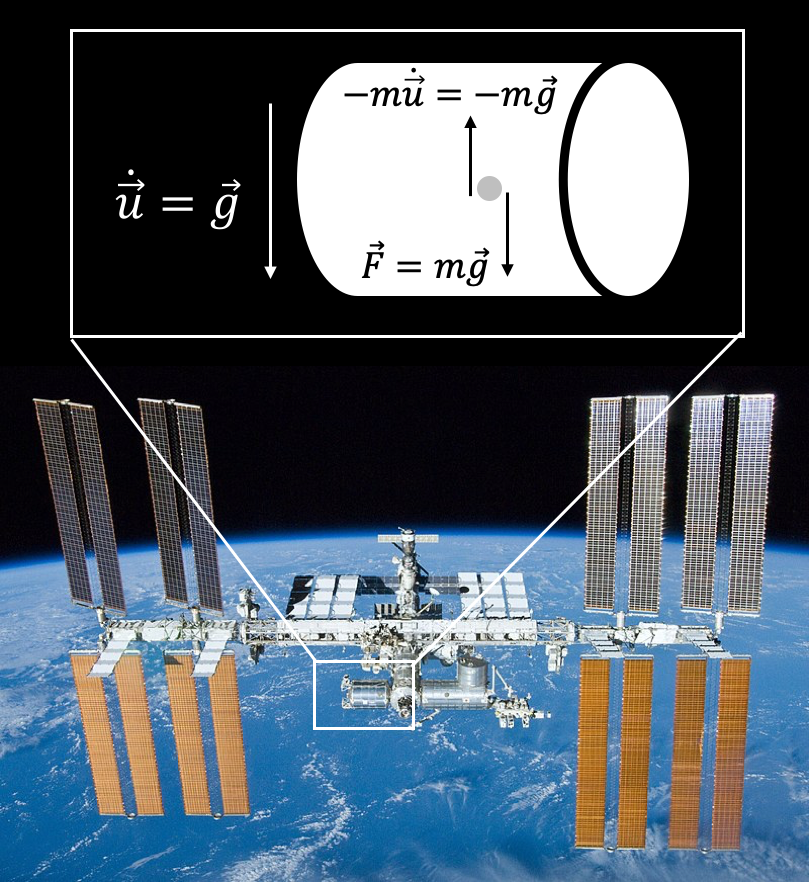
En el interior de la estación espacial internacional, por ejemplo, los cuerpos que flotan en el aire experimentan solo una fuerza aplicada: aquella debida a la interacción gravitacional con la Tierra (asumimos que la fuerza gravitacional de los astronautas y la estación es completamente despreciable). Esta fuerza no es despreciable y es igual a su peso medido a la altura de la estación (ver Figura (iss_microgravedad))$^1$.

Figura 5.53. Explicación de la experiencia de ingravidez en el interior de un vehículo espacial, en este caso un módulo de la Estación Espacial Internacional. El módulo corresponde a un sistema de referencia no inercial con una aceleración $

Ahora bien, la fuerza resultante sobre los mismos cuerpos, medida en el sistema de referencia de la estación, será igual, en virtud de la Ec. F_aplicada_no_inercial, a su peso (la fuerza aplicada) más una fuerza ficticia que apunta en dirección contraria al centro de la Tierra (que es hacia donde apunta la aceleración de la estación $\dot{\vec{u}}$) y que es en magnitud proporcional a esa misma aceleración. Dado que la aceleración de la estación es justamente la aceleración de la gravedad a esa altura, la fuerza aplicada sobre los cuerpos y la fuerza ficticia tendrán la misma magnitud.

Como resultado, en el sistema de referencia de la estación los cuerpos no experimentaran ninguna fuerza resultante y si se colocan en reposo, permaneceran así, incluso si nada los sostiene. Esta es justamente la razón de la ilusión de ingravidez que se percibe dentro de la estación y otros vehículos espaciales que orbitan nuestro planeta.

5.5.2. Sistemas de referencia rotantes

En los sistemas de referencia acelerados descritos en el apartado anterior la dirección de los ejes coordenados no cambia en el tiempo con respecto al sistema de referencia inercial. La rotación de los ejes, es una segunda forma de producir un sistema de referencia no inercial.

Si suponemos, por simplicidad, que el origen de los sistemas $R$ y $R'$ coinciden durante todo el tiempo, pero los ejes de coordenadas $\hat{e}_x'$, $\hat{e}_y'$, $\hat{e}_z'$ rotan respecto a un eje arbitrario, la regla de transformación entre las variables cinemáticas y dinámicas básicas será:

\begin{eqnarray} \nonumber t' & = & t \\ \nonumber \vec r' & = & \vec r\\ \nonumber m' & = & m \end{eqnarray}

En particular, si bien los vectores $\vec r$ y $\vec r'$ serán geométricamente idénticos, sus componentes no lo serán:

$$ x {\hat e_x} + y {\hat e_y} + z {\hat e_z} = x' {\hat e_x}' + y' {\hat e_y}' + z' {\hat e_z}' $$

Esta condición no es única para el vector posición $\vec r$ sino que aplica para cualquier cantidad vectorial $\vec A$ que definamos en el sistema:

\begin{equation} \label{eq:A_noinercial} A_x {\hat e_x} + A_y {\hat e_y} + A_z {\hat e_z} = A_{x'} {\hat e_x}' + A_{y'} {\hat e_y}' + A_{z'} {\hat e_z}' \end{equation}

Nótese que no hemos escrito $A_x'$ (dando a entender que el vector $\vec A$ cambia al cambiar de sistema de coordenadas) sino $A_{x'}$ para indicar que son sus componentes las que cambian.

¿Cómo se relacionan las razones de cambio de $(\mathrm{d}\vec A/\mathrm{d}t)$ y $(\mathrm{d}\vec A/\mathrm{d}t)'$ medidas en ambos sistemas de referencia?

Si derivamamos ambos lados de la Ec. (A_noinercial) obtenemos:

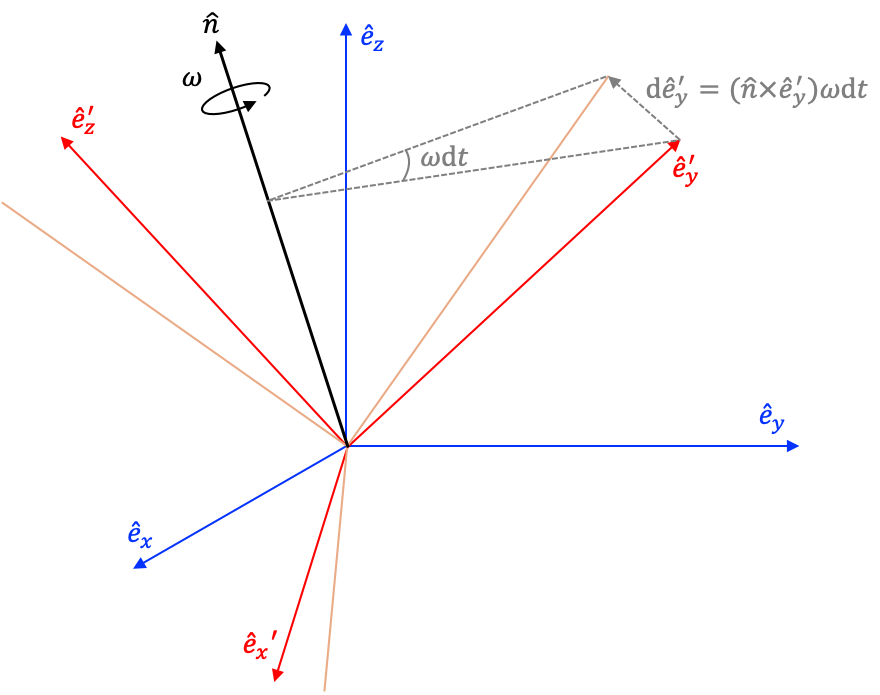
\begin{eqnarray} \label{eq:derivada_vector_rotacion_explicita} \frac{\mathrm{d}A_x}{\mathrm{d}t} {\hat e_x} + \frac{\mathrm{d}A_y}{\mathrm{d}t} {\hat e_y} + \frac{\mathrm{d}A_z}{\mathrm{d}t} {\hat e_z} & = & \frac{\mathrm{d}A_{x'}}{\mathrm{d}t} {\hat e_x}' + \frac{\mathrm{d}A_{y'}}{\mathrm{d}t} {\hat e_y}' + \frac{\mathrm{d}A_{z'}}{\mathrm{d}t} {\hat e_z}' +\\ \nonumber & & + A_{x'} \frac{\mathrm{d}{\hat e_x}'}{\mathrm{d}t} + A_{y'} \frac{\mathrm{d}{\hat e_y}'}{\mathrm{d}t} + A_{z'} \frac{\mathrm{d}{\hat e_z}'}{\mathrm{d}t} \end{eqnarray}

Los vectores unitarios coordenados en el sistema rotante varían dependiendo del valor instantáneo de la velocidad angular así $\omega(t)$ (ver Figura (rotacion_ejes)):

\begin{eqnarray} \mathrm{d}\hat{e_x}' & = & \vec{\omega}\times \hat{e_x}' \mathrm{d}t\\ \mathrm{d}\hat{e_y}' & = & \vec{\omega}\times \hat{e_y}' \mathrm{d}t\\ \mathrm{d}\hat{e_z}' & = & \vec{\omega}\times \hat{e_z}' \mathrm{d}t\\ \end{eqnarray}

donde $\vec \omega \equiv \omega \hat n$.

Figura 5.54. Construcción geométrica usada para calcular el cambio en la dirección de los vectores unitarios coordenados de un sistema de coordenadas cuando se produce una rotación alrededor de un eje arbitrario $

Nota: No hay vectores de rotación. A pesar de que en lo que sigue usaremos la notación $\vec\omega$ para referirnos a la cantidad $\omega\hat n$, es importante resaltar el hecho que no existe en matemáticas nada que podamos llamar un vector de rotación.

Como señalamos en la Sección Conjuntos, tuplas y vectores los vectores geométricos forman un espacio vectorial, sobre cuyos elementos esta definida una operación interna (la suma vectorial en este caso) que cumple una serie de condiciones matemáticas, entre ellas la conmutatividad: el orden en el que se realice una suma de vectores no debería alterar el resultado de la misma.

Si definimos dos rotaciones que se producen con tasas $\omega_1$ y $\omega_2$ alrededor de ejes diferentes $\hat n_1$ y $\hat n_2$ y queremos determinar el efecto que tienen en un tiempo $t$ las dos rotaciones sobre un vector dado (por ejemplo uno de los vectores unitarios en la Figura (rotacion_ejes)) no es posible:

1. Definir un "vector de rotación" $\vec\Omega=\Omega\hat N$ que represente la operación resultante. Es decir $\vec\Omega\neq \vec\omega_1+\vec\omega_2$.
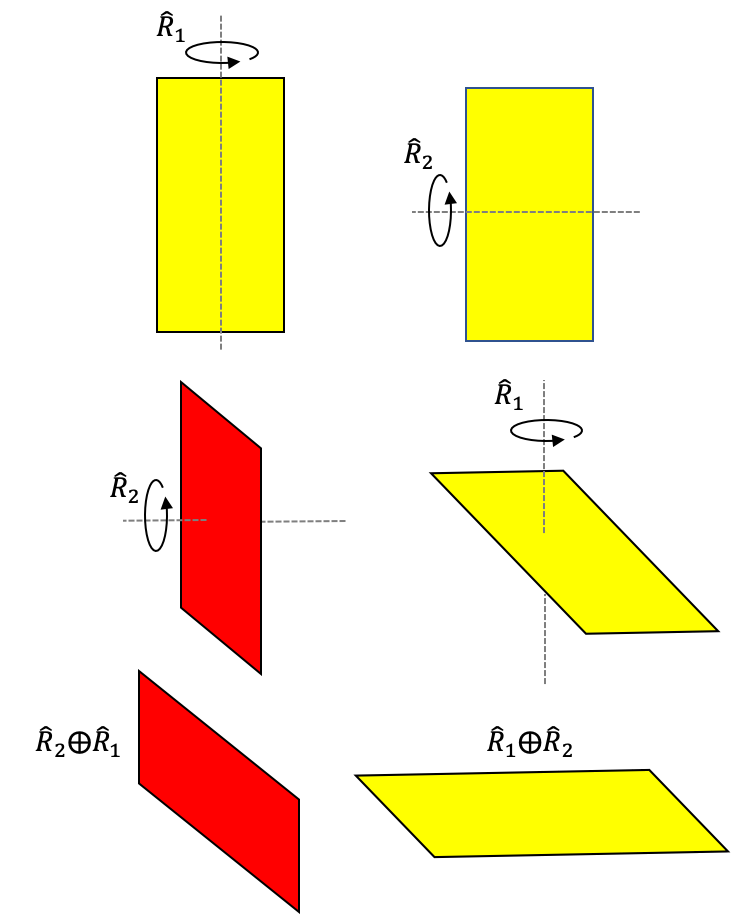
2. Incluso en el caso en el que, de forma ingeniosa o para un caso muy particular, pudiéramos definir dicha suma, la conmutatividad no podría asegurarse de forma general: las rotaciones no son conmutativas (ver Figura (rotaciones_no_conmutativas)).

Figura 5.55. Las rotaciones, representadas aquí por $

Con esto la tasa de cambio descrita por la Ec. (derivada_vector_rotacion_explicita) se puede escribir de la forma:

\begin{equation} \label{eq:derivada_vector_rotacion} \frac{\mathrm{d}}{\mathrm{d}t}\vec A = \frac{\mathrm{d}'}{\mathrm{d}t}\vec A+\vec\omega\times \vec A \end{equation}

donde por los operadores diferenciales $\mathrm{d}/\mathrm{d}t$ o $\mathrm{d}'/\mathrm{d}t$ entenderemos aquí, aquellos que solo actúan sobre las componentes en el sistema de referencia correspondiente, pero no sobre la dirección de los ejes. Así:

$$ \frac{\mathrm{d}'}{\mathrm{d}t}\vec A \equiv \frac{\mathrm{d}A_{x'}}{\mathrm{d}t} {\hat e_x}' + \frac{\mathrm{d}A_{y'}}{\mathrm{d}t} {\hat e_y}' + \frac{\mathrm{d}A_{z'}}{\mathrm{d}t} {\hat e_z}' $$

Por otro lado también es importante aclarar que las cantidades en el lado derecho de la Ec. (derivada_vector_rotacion) deben escribirse en el sistema de coordenadas rotante, es decir:

\begin{equation} \label{eq:omega_times_A} \vec\omega\times \vec A = \vec\omega\times(A_{x'} {\hat e_x}' + A_{y'} {\hat e_y}' + A_{z'} {\hat e_z}') \end{equation}

Dado que la Ec. (derivada_vector_rotacion) es válidad para cualquier vector libre, podemos definir una regla de transformación general para la derivada con respecto al tiempo de vectores, introduciendo el operador diferencial:

\begin{eqnarray} \frac{d}{dt} = \frac{d'}{dt}+\vec\omega\;\times \end{eqnarray}

donde se entiende que la cantidad derivada es una cantidad vectorial.

5.5.3. Adición de velocidades en sistemas rotantes

Usando estos resultados generales podemos encontrar ahora las reglas de transformación para la velocidad y la aceleración (los análogos a las Ecs. v_no_inercial y a_no_inercial).

En el caso de la velocidad:

$$ \vec v \equiv \frac{\mathrm{d}}{\mathrm{d}t}\vec r = \frac{\mathrm{d'}}{\mathrm{d}t}\vec r + \vec\omega\times\vec r $$

Por definición, sin embargo:

$$ \vec v'\equiv \frac{\mathrm{d'}\vec r}{\mathrm{d}t} $$

es decir, esta cantidad corresponde a la velocidad de la partícula medida en el sistema rotante.

De otro lado $\omega\times\vec r$ debe ser obligatoriamente escrito en términos de los vectores unitarios coordenados del sistema $R'$ (ver Ec. omega_times_A):

$$ \omega\times\vec r=\omega\times(x'\hat e_x'+y'\hat e_y'+z'\hat e_z')=\omega\times\vec r' $$

Con estas definiciones, la ley de "adición" de velocidades para un sistema de referencia rotante se escribe finalmente como:

\begin{equation} \label{eq:adicion_velocidades_rotante} \vec v = \vec v' + \vec\omega\times\vec r' \end{equation}

Nota: Vectores y componentes. Es muy importante entender que la Ecuación (adicion_velocidades_rotante) representa una relación entre vectores, no entre sus componentes. Es decir, esta relación implica por ejemplo que las magnitudes $|\vec v|$ y $|\vec v' + \vec\omega\times\vec r'|$ son iguales, puesto que se trata de una propiedad vectorial. Sin embargo, las componente $x$ en ambos sistemas de referencia no pueden compararse:

$$ v_x \neq v_{x'}+(\vec\omega\times\vec r')_{x'} $$

Las componentes de los vectores a ambos lados de la Ec. (adicion_velocidades_rotante) se relacionan a través de una matriz de rotación como se explico en la Sección Rotación de las cónicas en el plano. En la Sección Un ejemplo numérico de este mismo capítulo ilustraremos este importante punto.

5.5.4. Aceleraciones ficticias en sistemas rotantes

Para encontrar la relación entre las acleraciones, basta aplicar un procedimiento similar al anterior:

$$ \vec a \equiv \frac{\mathrm{d}}{\mathrm{d}t}\vec v = \frac{\mathrm{d'}}{\mathrm{d}t}\vec v + \vec\omega\times\vec v $$

sin embargo las componentes del vector $\vec v$ en el sistema de ejes de $R'$, que son las que deben usarse en el lado derecho de la ecuación anterior, ya no obedecen reglas tan simples como las de cualquier otro vector libre, tal como el vector $\vec r$.

Estas componentes obedecen la regla más compleja expresada por la Ec. (adicion_velocidades_rotante). Reemplazando las componentes de la velocidad medidas en el sistema inercial, las aceleraciones se relacionan como:

$$ \vec a = \frac{\mathrm{d'}}{\mathrm{d}t}(\vec v' + \vec\omega\times\vec r') + \vec\omega\times(\vec v' + \vec\omega\times\vec r') $$

Derivando y reuniendo términos semejantes obtenemos:

$$ \vec a = \vec a'+\vec\omega\times(\vec\omega\times \vec r')+2 \vec \omega\times\vec v'+ \dot{\vec{\omega}}\times \vec r' $$

donde

$$ \vec a'\equiv\frac{\mathrm{d'}}{\mathrm{d}t}\vec v'=\frac{\mathrm{d}v_{x'}}{\mathrm{d}t} {\hat e_x}' + \frac{\mathrm{d}v_{y'}}{\mathrm{d}t} {\hat e_y}' + \frac{\mathrm{d}v_{z'}}{\mathrm{d}t} {\hat e_z}' $$

es la aceleración instantánea que experimenta la partícula medida en el sistema rotante.

Si despejamos $\vec a'$ (a la manera como lo hicimos para deducir la Ec. a_no_inercial), obtenemos:

\begin{equation} \label{eq:ley_adicion_aceleraciones} \vec a' = \vec a-\vec\omega\times(\vec\omega\times \vec r')-2 \vec \omega\times\vec v'-\dot{\vec{\omega}}\times \vec r' \end{equation}

A diferencia de lo que observamos en sistemas no inerciales de ejes fijos, donde en la dinámica emerge una sola aceleración ficticia que es antiparalela a la aceleración del sistema de referencia ($-\dot{\vec{u}}$), en sistemas rotantes hay tres diferentes aceleraciones ficticias:

Figura 5.56. Explicación esquemática del origen y dirección de las aceleraciones centrífuga y de Coriolís.

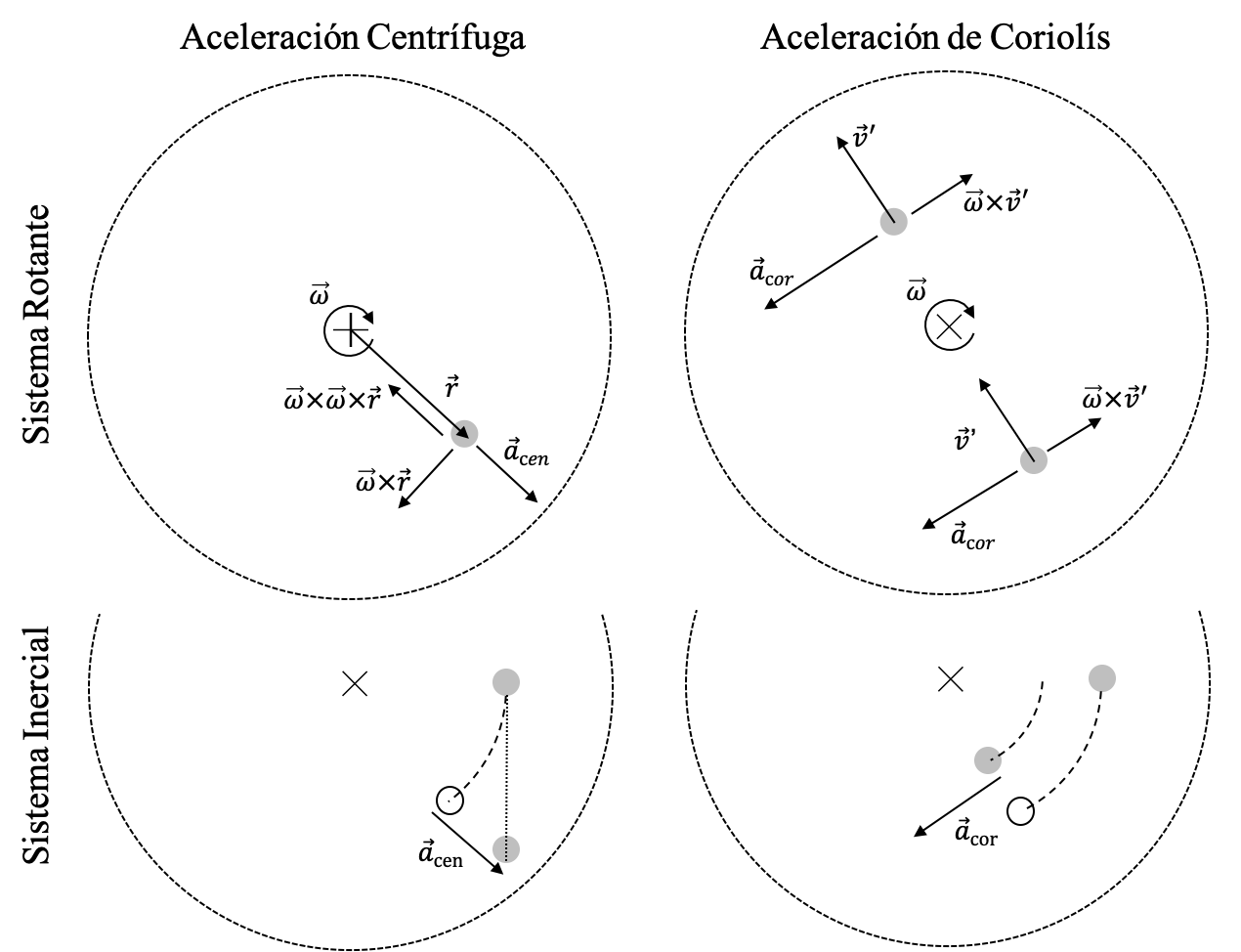
• $\vec{a}_\mathrm{cen}=-\vec\omega\times(\vec\omega\times\vec r')$. Esta aceleración apunta siempre en dirección contraria al eje de rotación (ver diagrama superior izquierdo en la Figura (aceleraciones_ficticias)). Por la misma razón se conoce como aceleración centrífuga. En términos inerciales, la aceleración centrífuga es una manifestación de la tendencia de las partículas a mantener su dirección de movimiento (ver diagrama inferior izquierdo en la Figura (aceleraciones_ficticias)). Visto desde el sistema rotante esta condición se manifiesta como una tendencia de las partículas a alejarse del eje de rotación.

• $\vec{a}_\mathrm{cor}=-2\vec\omega\times\vec v'$. Esta aceleración apunta siempre en dirección perpendicular a la velocidad de la partícula (medida en el sistema rotante) y puede ser contraria o en el mismo sentido a la dirección de rotación del sistema de referencia (ver diagrama superior derecho en la Figura (aceleraciones_ficticias)). Por razones históricas se conoce esta aceleración ficticia como aceleración de Laplace o más frecuentemente como aceleración de Coriolís (¡atención al acento final!) en honor al matemático y científico francés Gaspard-Gustave Coriolis ("Coriolís", ver recuardo Un poco de historia: Coriolís y la aceleración sin nombre). En términos inerciales, la aceleración de Coriolís es una manifestación de la tendencia de los cuerpos a mantener su velocidad de rotación al cambiar a puntos del sistema que se mueven con velocidad diferente (ver diagrama superior derecho en la Figura (aceleraciones_ficticias)). Si el cuerpo esta en reposo en el sistema rotante $\vec v'=\vec o$, no habrá ninguna aceleración de Coriolís. Si el cuerpo se mueve en dirección a puntos que rotan más lentamente ($\vec v'$ apunta en dirección al eje de rotación como en la parte inferior derecho de la Figura (aceleraciones_ficticias)) la partícula tiende a adelantarse. Al contrario, si la partícula se mueve a puntos del sistema que se mueven más rápidamente ($\vec v'$ dirigida hacia afuera), la partícula tenderá a retrasarse.

• $\vec{a}_\mathrm{euler}=-\dot{\vec{\omega}}\times \vec r'$. Esta aceleración se produce únicamente si la velocidad angular del sistema rotante cambia de magnitud. Por razones históricas se conoce como aceleración de Euler. En términos inerciales, la aceleración de Euler es una manifestación de la tendencia de los cuerpos a mantener la velocidad angular que traía el sistema rotante justo un instante antes. Así, si la aceleración angular aumenta, los cuerpos tenderán a retrasarse (a conservar la velocidad menor que traían) y su aceleración se producirá en dirección contraria a la dirección de rotación. Al contrario, si la aceleración angular disminuye, los cuerpos tenderán a acelerarse en la dirección de la rotación.

Un poco de historia: Coriolís y la aceleración sin nombre. La historia del descubrimiento de la que llamamos hoy la aceleración de Coriolís es una de las más curiosas e interesantes de la historia de la mecánica (Graney, 2011,Gerkema & Gostiaux, 2012)

Hoy sabemos que el efecto de esta aceleración sobre el movimiento de cuerpos en la superficie de una Tierra en rotación, fue descrito por primera vez en 1651 en el libro Almagestum Novum del astrónomo italiano Giovanni Battista Riccioli ("Richioli").

Con el propósito de probar que la Tierra no rotaba (Riccioli apoyaba una forma de teoría geocéntrica), el astrónomo italiano propuso el siguiente experimento mental: láncese un proyectil desde un punto en el ecuador de una Tierra que rota en dirección al norte. ¿Caerá el proyectil sobre el meridiano del lugar desde el que fue lanzado?

La respuesta ofrecida por Riccioli utiliza un razonamiento similar a aquel que aparece representado en el diagrama abajo a la derecha en la Figura (fuerzas_ficticias). Si la Tierra rota, el cañón en el ecuador se moverá (respecto a un sistema inercial externo) hacia el oriente, más rápido que cualquier punto en una latitud mayor (más cerca al eje de rotación). De este modo, al avanzar hacia el norte el proyectil irá sobrepasando (por su velocidad mayor) los puntos de la superficie que están debajo de él. Al final, la bala caerá al oriente del meridiano desde el que fue lanzado. En términos modernos, el proyectil sufré una aceleración que va en la misma dirección de rotación de la Tierra (hacia el oriente).

Como el efecto no había sido observado hasta la fecha, Riccioli pensó que se trataba de un poderoso argumento en contra de la idea de una Tierra en rotación. Curiosamente (y sin proponérselo), miembros de la Accademia del Cimento en Italia, observaron pocos años después la aceleración anómala descrita por Riccioli al estudiar el movimiento de péndulos. Y es que el cuerpo suspendido en el péndulo se comporta como una bala de cañón. Si suponemos que oscila inicialmente moviéndose del ecuador hacia el norte la tendencia a desplazarse al oriente hará que el plano de oscilación cambie en el sentido de las manecillas del reloj. En las notas de la academia de la década de 1660 quedo registrado la observación sistemática de este efecto. Los académicos no pudieron explicar el fenómeno pero tampoco lograron asociarlo con la "predicción de Riccioli". No fue sino hasta 1851 cuando el mismo experimento fue repetido bajo condiciones controladas (y con el conocimiento pleno de la existencia de la aceleración anómala descrita por Riccioli) por el astrónomo francés León Foucault ("Fuco").

La misma aceleración análoga predicha originalmente por Riccioli fue descrita para distintas condiciones (cuerpos en caída libre, cuerpos lanzados hacia arriba, cuerpos lanzados hacia el oriente) en trabajos posteriores durante el mismo siglo por astrónomos y físicos como Giovanni Borelli (1668), Claude Dechales (1674) e incluso el mismo Isaac Newton en camino a su formulación de la teoría de gravitación universal (1680).

Una teoría rigurosa y completa de esta aceleración anómala solo llegó a ser formulada hasta 1798 por Pierre-Simon Laplace, quién la presento como parte de su obra cumpre Tratado de Mecánica Celeste y en relación con su estudio del fenómeno de las mareas lunisolares. La descripción de Laplace fue tan completa que para hacer justicia deberíamos llamar a esta la aceleración de Laplace.

En el año 1835, el matemático y científico francés Gaspard-Gustave Coriolis, en un artículo en francés titulado "Disertación sobre las ecuaciones de movimiento relativo de los sistemas corporales" (Coriolis, 1835), presentó la formula general que dedujimos en esta sección para $\vec a_\mathrm{cor}$ y a la que llamo "fuerza centrífuga compuesta". El objetivo de Corilís erá estudiar las distintas aceleraciones ficticias que se producen en los fluídos en sistemas mecánicos en rotación (tales como las ruedas de molino movidas por agua).

Si bien el resultado de Corilís no atrajo mucho la atención por al menos cuatrro décadas, no fue sino hasta 1879 cuando algunos físicos, estudiando problemas mecánicos locales, incluyendo el péndulo de Foucault, empezaron a identificar esta aceleración con el nombre de Coriolís. Ya para el año 1912, y en el contexto de trabajos relacionados con las fuerzas dentro de fluídos en movimiento, la aceleración era conocida en la literatura como aceleración de Coriolís o Fuerza de Coriolís.

Figura 5.57. Gaspard-Gustave Coriolis (1792-1843) en un retrato de 1841. Coriolís tuvo la suerte de que una de las más importantes aceleraciones ficticias que se producen en sistemas en rotación, y que habían sido identificada y descritas antes por varios físicos desde Laplace hasta Riccioli, llevara finalmente su nombre.

NOTAS AL PIE:

1. La estación espacial internacional se encuentra a apenas 400 km de altura sobre la superficie de la Tierra. Por lo tanto el peso de los cuerpos que transporta es apenas $6371^2/(6371+400)^2\approx 0.88$ veces el que experimentan en la superficie de la Tierra (6371 km es el radio promedio de la Tierra).

Indice | Previo: Mecanica.Dinamica.SistemaParticulas | Siguiente: Mecanica.SistemasNoInerciales.Numerico